2018杭电多校第一场补题1008 RMQ Similar Sequence 笛卡尔树

RMQ Similar Sequence

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 255535/255535 K (Java/Others)
Total Submission(s): 231    Accepted Submission(s): 41

 

Problem Description

Chiaki has a sequence A={a1,a2,…,an}. Let RMQ(A,l,r) be the minimum i (l≤i≤r) such that ai is the maximum value in al,al+1,…,ar.

Two sequences A and B are called \textit{RMQ Similar}, if they have the same length n and for every 1≤l≤r≤n, RMQ(A,l,r)=RMQ(B,l,r).

For a given the sequence A={a1,a2,…,an}, define the weight of a sequence B={b1,b2,…,bn} be ∑i=1nbi (i.e. the sum of all elements in B) if sequence B and sequence A are RMQ Similar, or 0 otherwise. If each element of B is a real number chosen independently and uniformly at random between 0 and 1, find the expected weight of B.

 

 

Input

There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
The first line contains an integer n (1≤n≤106) -- the length of the sequence.
The second line contains n integers a1,a2,…,an (1≤ai≤n) denoting the sequence.
It is guaranteed that the sum of all n does not exceed 3×106.

 

 

Output

For each test case, output the answer as a value of a rational number modulo 1e9+7.
Formally, it is guaranteed that under given constraints the probability is always a rational number pq (p and q are integer and coprime, q is positive), such that q is not divisible by 1e9+7. Output such integer a between 0 and 109+6 that p−aq is divisible by 1e9+7.

 

 

Sample Input

3

3

1 2 3

3

1 2 1

5

1 2 3 2 1

 

 

Sample Output

250000002

500000004

125000001

 

题目意思

先给你一个a数组，然后b数组中的数字都是0~1之间的实数，定义B的权值为每个数组中每个数字权值之和，问你要使得a,b数组的区间最大值的位置相同的b的权值的期望值。

首先分析每个数组当中每个点，既然是0~1之间的实数，这个点的数学期望值就是1（积分得来）,整个数组的权值期望即为n/2。

好了，现在我们考虑RMQ相同，这个时候需要补一下一个神奇的树：笛卡尔树

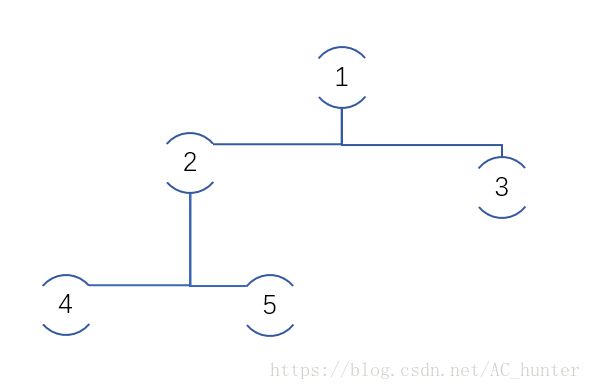
简单这么理解一下吧，对原序列构造一棵树，第一个条件是让权值大的（这题是大，也可以是小）放在上面，即作为父节点，二级条件就是下标小的在左边，下标大的在右边（考虑把一个数组拉成树，权值大的拎上去，子节点为它相邻的左右元素）。

既然a数组和b数组RMQ相同，那么他们的笛卡尔树也相同。

O(n)算法构建出来这颗神奇滴树，下面就开始玩期望了。

既然是0~1之间的实数，那么可选择的数字就非常多了，那么，有两个数字相同的概率就是0对吧。

那么，这n个数字各不相同，那么就有n个大小不同的数了，那么怎么选择数字呢，我们来画个树分析一下

 

对于1号节点，它下面总共有4个后代们，加上它自己，就总共有5个点，根据定义，要使得1号节点（最小or最大），那么就有1/5的期望，然后我们打掉1号节点，剩下的节点也能这么分析对吧，所以期望就是 ，Size[i]是以i节点为根的数的节点数量。

然后，答案就这么出来了。

 *n/2

然后，我补题时候被一个小坑卡了会（很久），就是，虽然b数组的中没有重复的元素，但a数组中可以有重复的元素呀，愚蠢的我构建笛卡尔树是按照没有重复元素的方法构建滴（就是少加了个=号），然后，当插入相同元素的点的时候，就会GG（爆栈），一个小坑，Mark了。

最后，附上代码：

#include
using namespace std;
const int maxn = 1e6+10;
const long long ha = 1e9+7;
struct node{
    int l, r;
} t[maxn];
int a[maxn],n,root,num[maxn];
int sta[maxn], tail;
long long qm(long long a, long long b){
    long long ans=1;
    while(b){
        if (b&1){
            ans=ans*a%ha;
        }
        a=a*a%ha;
        b>>=1;
    }
    return ans;
}
void read_build(){
    scanf("%d",&n);
    int ex;
    tail=0;
    for (int i=1;i<=n;++i){
        num[i]=1; t[i].l=t[i].r=0;
        scanf("%d",&a[i]);
        if (tail==0){
            sta[tail]=i;    tail++; ;root=i;
            continue;
        }
        if (a[sta[tail-1]]>=a[i]){
            t[sta[tail-1]].r=i;
            sta[tail]=i;    tail++;
        }else{
            while(a[sta[tail-1]]