机器学习算法-DBSCAN聚类
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在有“噪声”的空间数据库中发现任意形状的聚类。
一、基础概念
在介绍算法之前,先明确几个在DBSCAN模型中常用的概念:
- 对象的 ϵ -临域:给定对象在半径 ϵ 内的区域。
- 对象:如果一个对象的 ϵ -临域至少包含最小数目 MinPts 个对象,则称该对象为核心对象。
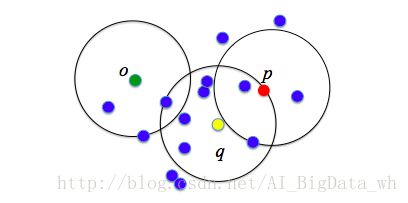
例如,在下图中, ϵ=1cm , MinPts=5 , q 是一个核心对象,而 p 不是, o 也不是。

- 直接密度可达:给定一个对象集合 D ,如果 p 是在 q 的ε-邻域内,而 q 是一个核心对象,我们说对象 p 从对象 q 出发是直接密度可达的。
例如,在下图中, ϵ=1cm , MinPts=5 , q 是一个核心对象,对象 p 从对象 q 出发是直接密度可达的,而对象 o 从对象 q 出发不是直接密度可达的。
- 密度可达的:如果存在一个对象链 p1 , p2 ,…, pn , p1=q , pn=p ,对 pi∈D ,( 1<=i<=n ), pi+1 是从 pi 关于和 MitPts 直接密度可达的,则对象 p 是从对象 q 关于 ϵ 和 MinPts 密度可达的。
例如,在下图中, ϵ=1cm , MinPts=5 , q 是一个核心对象, o 是从 q 关于 ϵ 和 MitPts 直接密度可达, p 是从 o 关于ε和 MitPts 直接密度可达,则对象 p 从对象 q 关于 ϵ 和 MinPts 密度可达的。
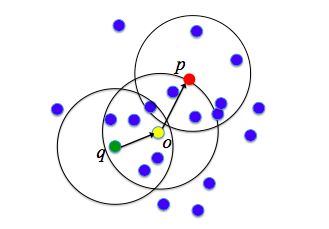
- 密度相连的:如果对象集合 D 中存在一个对象 o ,使得对象 p 和 q 是从 o 关于 ϵ 和 MinPts 密度可达的,那么对象 p 和 q 是关于 ϵ 和 MinPts 密度相连的。
- 噪声: 一个基于密度的簇是基于密度可达性的最大的密度相连对象的集合。不包含在任何簇中的对象被认为是“噪声”。如下图中的对象 N 便是噪声。

二、DBSCAN算法
DBSCAN通过检查数据集中每个对象的 ϵ -邻域来寻找聚类。如果一个点的 ϵ -邻域包含多于 MinPts 个对象,则创建一个以该点作为核心对象的新簇。然后DBSCAN反复地从这些核心对象直接密度可达的对象寻找最大密度相连对象集合,这个过程可能涉及一些密度可达簇的合并。一直运行到当没有新的点可以被添加到任何簇时,该过程结束。DBSCAN算法描述:
输入:包含 n 个对象的数据库,半径 ϵ ,最少数目 MinPts 。
输出:所有生成的簇,达到密度要求。
1. REPEAT
2. 判断输入点是否为核心对象;
3. IF 抽出的点是核心点
THEN 找出所有从该点密度可达的对象。
4. UNTIL 所有输入点都判断完毕。
5. REPEAT
6. 针对所有核心对象的 ϵ -邻域所有直接密度可达点, 找到最大密度相连对象集合,中间涉及一些密度可达对象的合并。
7. UNTIL 所有核心对象的 ϵ -邻域都被遍历。
看上面的介绍,很多人会觉得晕晕的。还是没有理清算法到底与第一部分介绍的核心对象、密度可达、密度相连等概念有什么关系。接下来用白话给大家解释一下。仔细观察上面的步骤介绍,会发现DBSCAN在新生成每个簇时主要分三步进行:一是确定核心对象;二是找到该核心对象密度可达的所有对象;三是对于密度可达对象找到最大密度相连对象集合,即为生成的簇。
三、DBSCAN算法举例
下面给出一个样本事务数据库,对它实施DBSCAN算法。
| 序号 | 属性1 | 属性2 |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 4 | 0 |
| 3 | 0 | 1 |
| 4 | 1 | 1 |
| 5 | 2 | 1 |
| 6 | 3 | 1 |
| 7 | 4 | 1 |
| 8 | 5 | 1 |
| 9 | 0 | 2 |
| 10 | 1 | 2 |
| 11 | 4 | 2 |
| 12 | 1 | 3 |
根据所给的数据通过对其进行DBSCAN算法,以下为算法的步骤(设 n=12 ,用户输入 ϵ=1 , MinPts=4 ) 。
| 序号 | 属性1 | 属性2 | ϵ -邻域的个数 | 是否为核心点 | 核心点可达到点的集合 |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 2 | × | |
| 2 | 4 | 0 | 2 | × | |
| 3 | 0 | 1 | 3 | × | |
| 4 | 1 | 1 | 5 | √ | 1,3,4,5,10 |
| 5 | 2 | 1 | 3 | × | |
| 6 | 3 | 1 | 3 | × | |
| 7 | 4 | 1 | 5 | × | 2,6,7,8,11 |
| 8 | 5 | 1 | 2 | √ | |
| 9 | 0 | 2 | 3 | × | |
| 10 | 1 | 2 | 4 | √ | 4,9,10,12 |
| 11 | 4 | 2 | 2 | × | |
| 12 | 1 | 3 | 2 | × |
样本4可达样本10,样本10可达样本(4,9,10,12),因此样本4的可达点和集合与样本10的可达点的集合是密度相连的。因此这两个可达点的集合可以合并为一个簇。最终的聚类结果为{1,3,4,5,9,10,12}为一个簇;而{2,6,7,8,11}为一个簇。
四、DBSCAN算法优缺点
密度聚类方法的指导思想是,只要一个区域中的点的密度大于某个域值,就把它加到与之相近的聚类中去。这类算法能克服基于距离的算法只能发现“类球形”的聚类的缺点,可发现任意形状的聚类,且对噪声数据不敏感。而且不需要事先知道要形成的簇类的数量。
但计算密度单元的计算复杂度大,需要建立空间索引来降低计算量,且对数据维数的伸缩性较差。这类方法需要扫描整个数据库,每个数据对象都可能引起一次查询,因此当数据量大时会造成频繁的I/O操作。并且对于超参数 ϵ 和 MinPts 的选择没有固定标准,一般都是凭经验,不同的参数组合对最后的聚类效果有较大影响。
五、DBSCAN算法Python实战
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.datasets.samples_generator import make_blobs
center = [[1,1],[-1,-1],[1,-1]]
cluster_std = 0.3
X,labels = make_blobs(n_samples=2000,centers=center,n_features=2,cluster_std=cluster_std,random_state=0)
print('X.shape',X.shape) print("labels",set(labels)) plt.figure() plt.subplot(121) plt.plot(X[:,0],X[:,1],'o') plt.xlim([-2.5,2.5]) plt.ylim([-2.5,2.5]) plt.title("Raw Data") plt.subplot(122) y_pred = DBSCAN(eps=0.3, min_samples=10).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.xlim([-2.5,2.5]) plt.ylim([-2.5,2.5]) plt.title("DBSCAN Clustering") plt.show()
参考资料
- http://www.cnblogs.com/nolonely/p/6980160.html scikit-learn提供的自带的数据集
- http://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html#sphx-glr-auto-examples-cluster-plot-dbscan-py Demo of DBSCAN clustering algorithm
- http://www.cnblogs.com/hehheai/p/6509645.html 用scikit-learn学习DBSCAN聚类
- https://en.wikipedia.org/wiki/DBSCAN DBSCAN
- http://www.cnblogs.com/pinard/p/6208966.html DBSCAN密度聚类算法
- 举例部分是参考一个PPT课件,两年前下载梳理的,现在忘记PPT发布的位置。抱歉。在此对那位不知名的作者表示感谢。