史上第二详尽的平衡树(Splay)详解
谢鸣:本文来自zyf2000学姐的blog,原题为“史上最详尽的平衡树(splay)讲解与模板”,我在这里拿过来使用,命名为“史上第二详尽的平衡树(Splay)详解”,并加上了一些新的操作.
变量声明:f[i]表示i的父结点,ch[i][0]表示i的左儿子,ch[i][1]表示i的右儿子,key[i]表示i的关键字(即结点i代表的那个数字),cnt[i]表示i结点的关键字出现的次数(相当于权值),size[i]表示包括i的这个子树的大小;sz为整棵树的大小,root为整棵树的根。
再介绍几个基本操作:
【clear操作】:将当前点的各项值都清0(用于删除之后)
void clear(int x)
{
f[x]=cnt[x]=ch[x][0]=ch[x][1]=size[x]=key[x]=0;
}【get操作】:判断当前点是它父结点的左儿子还是右儿子
bool get(int x)
{//get一下该节点是左孩子还是右孩子
return ch[f[x]][1]==x;
}
【pushup操作】:更新当前点的size值(用于发生修改之后)
void pushup(int x)
{//更新这棵树的节点个数
if (x)
{
size[x]=cnt[x];
if (ch[x][0]) size[x]+=size[ch[x][0]];
if (ch[x][1]) size[x]+=size[ch[x][1]];
}
}下面boss来了:
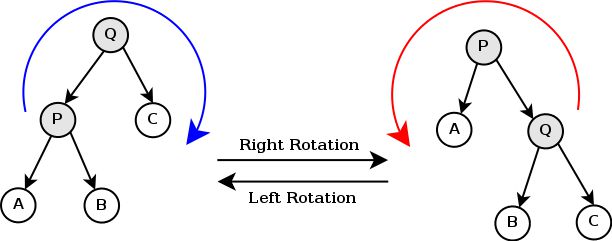
【rotate操作图文详解】
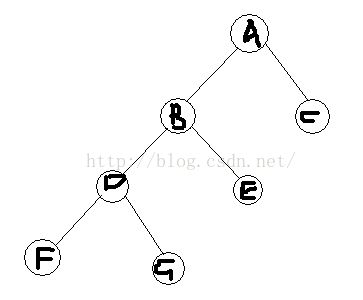
这是原来的树,假设我们现在要将D结点rotate到它的父亲的位置。
step 1:
找出D的父亲结点(B)以及父亲的父亲(A)并记录。判断D是B的左结点还是右结点。
step 2:
我们知道要将Drotate到B的位置,二叉树的大小关系不变的话,B就要成为D的右结点了没错吧?
咦?可是D已经有右结点了,这样不就冲突了吗?怎么解决这个冲突呢?
我们知道,D原来是B的左结点,那么rotate过后B就一定没有左结点了对吧,那么正好,我们把G接到B的左结点去,并且这样大小关系依然是不变的,就完美的解决了这个冲突。


这样我们就完成了一次rotate,如果是右儿子的话同理。step 2的具体操作:
我们已经判断了D是B的左儿子还是右儿子,设这个关系为K;将D与K关系相反的儿子的父亲记为B与K关系相同的儿子(这里即为D的右儿子的父亲记为B的左儿子);将D与K关系相反的儿子的父亲即为B(这里即为把G的父亲记为B);将B的父亲即为D;将D与K关系相反的儿子记为B(这里即为把D的右儿子记为B);将D的父亲记为A。
最后要判断,如果A存在(即rotate到的位置不是根的话),要把A的儿子即为D。
显而易见,rotate之后所有牵涉到变化的父子关系都要改变。以上的树需要改变四对父子关系,BG DG BD AB,需要三个操作(BG BD AB)。
step 3:update一下当前点和各个父结点的各个值
【代码】
void rotate(int x)
{
int old=f[x],oldf=f[old],which=get(x);
ch[old][which]=ch[x][which^1]; f[ch[old][which]]=old; //这两句的意思是:
//我的儿子过继给我的爸爸;同时处理父子两个方向上的信息
ch[x][which^1]=old; f[old]=x;
//我给我爸爸当爹,我爸爸管我叫爸爸
f[x]=oldf;//我的爷爷成了我的爸爸
if (oldf) ch[oldf][ch[oldf][1]==old]=x;
pushup(old); pushup(x);//分别维护信息
}【splay操作】
其实splay只是rotate的发展。伸展操作只是在不停的rotate,一直到达到目标状态。如果有一个确定的目标状态,也可以传两个参。此代码直接splay到根。
splay的过程中需要分类讨论,如果是三点一线的话(x,x的父亲,x的祖父)需要先rotate x的父亲,否则需要先rotate x本身`
void splay(int x)//splay树平衡
{
for (int fa; fa=f[x]; rotate(x))
if (f[fa])
rotate((get(x)==get(fa))?fa:x);//如果祖父三代连城一条线,就要从祖父哪里rotate
rt=x;
}【insert操作】
其实插入操作是比较简单的,和普通的二叉查找树基本一样。
step 1:如果root=0,即树为空的话,做一些特殊的处理,直接返回即可。
step 2:按照二叉查找树的方法一直向下找,其中:
如果遇到一个结点的关键字等于当前要插入的点的话,我们就等于把这个结点加了一个权值。因为在二叉搜索树中是不可能出现两个相同的点的。并且要将当前点和它父亲结点的各项值更新一下。做一下splay。
如果已经到了最底下了,那么就可以直接插入。整个树的大小要+1,新结点的左儿子右儿子(虽然是空)父亲还有各项值要一一对应。并且最后要做一下他父亲的update(做他自己的没有必要)。做一下splay。
void insert(int x)//x为权值
{
if (rt==0)
{
sz++; key[sz]=x; rt=sz;
cnt[sz]=size[sz]=1;
f[sz]=ch[sz][0]=ch[sz][1]=0;
return;
}
int now=rt,fa=0;
while (1)
{
if (x==key[now])//这个数在树中已经出现了
{
cnt[now]++; pushup(now); pushup(fa); splay(now); return;
}
fa=now; now=ch[now][key[now]if (now==0)
{
sz++;
size[sz]=cnt[sz]=1;
ch[sz][0]=ch[sz][1]=0;
ch[fa][x>key[fa]]=sz;//根据加入点的顺序重新标号
f[sz]=fa;
key[sz]=x;
pushup(fa); splay(sz); return;
}
}
} 【rnk操作】查询x的排名
初始化:ans=0,当前点=root
和其它二叉搜索树的操作基本一样。但是区别是:
如果x比当前结点小,即应该向左子树寻找,ans不用改变(设想一下,走到整棵树的最左端最底端排名不就是1吗)。
如果x比当前结点大,即应该向右子树寻找,ans需要加上左子树的大小以及根的大小(这里的大小指的是权值)。
不要忘记了再splay一下
int rnk(int x)
{
int now=rt,ans=0;
while (1)
{
if (x0];
else
{
ans+=size[ch[now][0]];
if (x==key[now])
{//此时x和树中的点重合,树中不允许有两个相同的点
splay(now); return ans+1;
}
ans+=cnt[now];
now=ch[now][1];//到达右孩子处
}
}
} 【kth操作】找到排名为x的点
初始化:当前点=root
和上面的思路基本相同:
如果当前点有左子树,并且x比左子树的大小小的话,即向左子树寻找;
否则,向右子树寻找:先判断是否有右子树,然后记录右子树的大小以及当前点的大小(都为权值),用于判断是否需要继续向右子树寻找。
int kth(int x)
{
int now=rt;
while (1)
{
if (ch[now][0] && x<=size[ch[now][0]])
now=ch[now][0];
else
{
int temp=size[ch[now][0]]+cnt[now];
if (x<=temp)
return key[now];
x-=temp; now=ch[now][1];
}
}
}【求x的前驱(后继),前驱(后继)定义为小于(大于)x,且最大(最小)的数】
这类问题可以转化为将x插入,求出树上的前驱(后继),再将x删除的问题。
其中insert操作上文已经提到。
【pre/next操作】
这个操作十分的简单,只需要理解一点:在我们做insert操作之后做了一遍splay。这就意味着我们把x已经splay到根了。求x的前驱其实就是求x的左子树的最右边的一个结点,后继是求x的右子树的左边一个结点(想一想为什么?)
int pre()//由于进行splay后,x已经到了根节点的位置
{//所以只要寻找左右子树最左边(或最右边的)数
int now=ch[rt][0];
while (ch[now][1]) now=ch[now][1];
return now;
}
int next()
{
int now=ch[rt][1];
while (ch[now][0]) now=ch[now][0];
return now;
}【del操作】
删除操作是最后一个稍微有点麻烦的操作。
step 1:随便find一下x。目的是:将x旋转到根。
step 2:那么现在x就是根了。如果cnt[root]>1,即不只有一个x的话,直接-1返回。
step 3:如果root并没有孩子,就说名树上只有一个x而已,直接clear返回。
step 4:如果root只有左儿子或者右儿子,那么直接clear root,然后把唯一的儿子当作根就可以了(f赋0,root赋为唯一的儿子)
剩下的就是它有两个儿子的情况。
step 5:我们找到新根,也就是x的前驱(x左子树最大的一个点),将它旋转到根。然后将原来x的右子树接到新根的右子树上(注意这个操作需要改变父子关系)。这实际上就把x删除了。不要忘了update新根。
void del(int x)
{
rnk(x);
if (cnt[rt]>1) {cnt[rt]--; pushup(rt); return;}//有多个相同的数
if (!ch[rt][0] && !ch[rt][1]) {clear(rt); rt=0; return;}
if (!ch[rt][0]) {
int oldrt=rt; rt=ch[rt][1]; f[rt]=0; clear(oldrt); return;
}
else if (!ch[rt][1]) {
int oldrt=rt; rt=ch[rt][0]; f[rt]=0; clear(oldrt); return;
}
int oldrt=rt; int leftbig=pre();
splay(leftbig);
ch[rt][1]=ch[oldrt][1];
f[ch[oldrt][1]]=rt;
clear(oldrt);
pushup(rt);
}完整代码
luogu3369【模板】普通平衡树
bzoj3224普通平衡树
/* f[i]:i节点的父节点,cnt[i]每个点出现的次数,ch[i][0/1]:0表示左孩子,1表示右孩子, size[i]表示以i为根节点的子树的节点个数 key[i]表示点i代表的数的值;sz为整棵树的节点个数,rt表示根节点 */
#includeif (now==0)
{
sz++;
size[sz]=cnt[sz]=1;
ch[sz][0]=ch[sz][1]=0;
ch[fa][x>key[fa]]=sz;//根据加入点的顺序重新标号
f[sz]=fa;
key[sz]=x;
pushup(fa); splay(sz); return;
}
}
}
int rnk(int x)//查询x的排名
{
int now=rt,ans=0;
while (1)
{
if (x0];
else
{
ans+=size[ch[now][0]];
if (x==key[now])
{//此时x和树中的点重合,树中不允许有两个相同的点
splay(now); return ans+1;
}
ans+=cnt[now];
now=ch[now][1];//到达右孩子处
}
}
}
int kth(int x)
{//查询排名为x的数
int now=rt;
while (1)
{
if (ch[now][0] && x<=size[ch[now][0]])
now=ch[now][0];
else
{
int temp=size[ch[now][0]]+cnt[now];
if (x<=temp)
return key[now];
x-=temp; now=ch[now][1];
}
}
}
int pre()//由于进行splay后,x已经到了根节点的位置
{//所以只要寻找左右子树最左边(或最右边的)数
int now=ch[rt][0];
while (ch[now][1]) now=ch[now][1];
return now;
}
int next()
{
int now=ch[rt][1];
while (ch[now][0]) now=ch[now][0];
return now;
}
void del(int x)
{
rnk(x);
if (cnt[rt]>1) {cnt[rt]--; pushup(rt); return;}//有多个相同的数
if (!ch[rt][0] && !ch[rt][1]) {clear(rt); rt=0; return;}
if (!ch[rt][0]) {
int oldrt=rt; rt=ch[rt][1]; f[rt]=0; clear(oldrt); return;
}
else if (!ch[rt][1]) {
int oldrt=rt; rt=ch[rt][0]; f[rt]=0; clear(oldrt); return;
}
int oldrt=rt; int leftbig=pre();
splay(leftbig);
ch[rt][1]=ch[oldrt][1];
f[ch[oldrt][1]]=rt;
clear(oldrt);
pushup(rt);
}
int main()
{
int n;
scanf("%d",&n);
for (int i=1; i<=n; i++)
{
int type,k;
scanf("%d%d",&type,&k);
if (type==1) insert(k);
if (type==2) del(k);
if (type==3) printf("%d\n",rnk(k));
if (type==4) printf("%d\n",kth(k));
if (type==5)
{
insert(k); printf("%d\n",key[pre()]); del(k);
}
if (type==6)
{
insert(k); printf("%d\n",key[next()]); del(k);
}
}
} 区间操作 文艺平衡树
Splay的区间翻转:
【建树操作】
注意建树每次返回根节点的编号
区分一个节点的排名和这个节点的值:这个节点的排名是它是当前数组中的第几个,用左儿子的size+1表示;这个节点的值是题目中输入的数字,在本题中是1~n;
增加数字为1和n+2的两个哨兵节点,因为如果对区间1~x或 x~n操作,用到前后的节点就需要1和n+2。
在main函数中
for (int i=1; i<=n; i++) data[i+1]=i;
data[1]=-inf; data[n+2]=inf;
rt=build_tree(0,1,n+2);build_tree:
int build_tree(int fa,int l,int r)
{
if (l>r) return 0;
int mid=(l+r)>>1;
int now=++sz;
key[now]=data[mid]; f[now]=fa; tag[now]=0;
ch[now][0]=build_tree(now,l,mid-1);
ch[now][1]=build_tree(now,mid+1,r);
pushup(now);
return now;
}【下传标记】
每到一个新节点都要pushdown
void pushdown(int x)
{
if (x && tag[x])
{
tag[ch[x][0]]^=1;
tag[ch[x][1]]^=1;
swap(ch[x][0],ch[x][1]);
tag[x]=0;
}
}【splay操作】
与普通的splay没有什么不同,比上面的goal加了一个目标goal而已
void splay(int x,int goal)//比上面的goal加了一个目标goal而已
{
for (int fa; (fa=f[x])!=goal; rotate(x))
if (f[fa]!=goal)
rotate((get(x)==get(fa))?fa:x);
if (!goal) rt=x;
}最重要的来了
【turn翻转区间】
首先,也是最重要的,我们认为伸展树中序遍历即是我们维护的序列!什么意思呢?比如有数据在数组中这样存放:a[5]={5,4,3,1,2};那么存入伸展树后,再中序遍历的结果应该还是:{5,4,3,1,2}。即下标从小到大,而不是里面的值从小到大!这是与SBT树最大的不同!
原理:若要翻转[l+1, r+1],将r+2 Splay到根,将l Splay到 r+2 的左儿子,然后[l+1, r+1]就在根节点的右子树的左子树位置了,给它打上标记(理解是否有误?)
来看图片:
step1
step2
使r+2旋转到根,
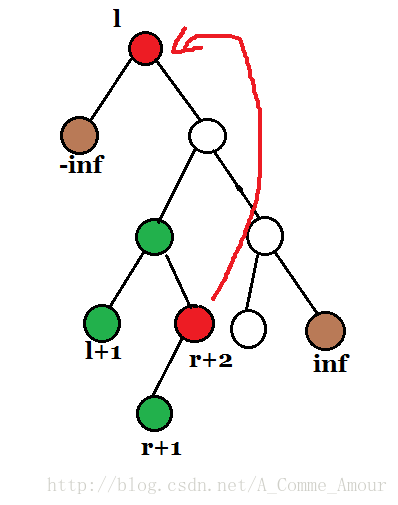
由于l < r+2,此时l成了r+2的左子树,那么r+2的右子树的左子树即为所求得区间,我们就可以对这棵子树随意操作了!比如删除整个区间,区间内的每个数都加上x,区间翻转,区间旋转等。
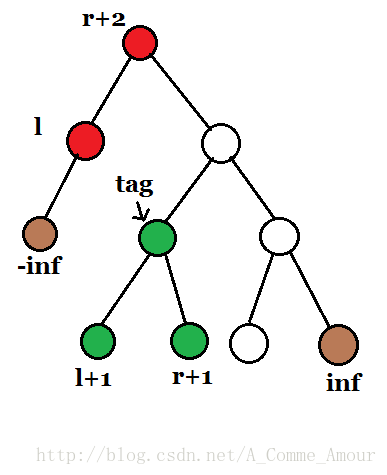
其他操作
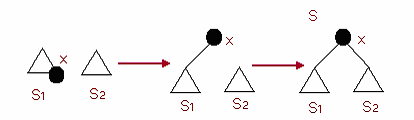
Join(S1,S2):将两个伸展树S1与S2合并成为一个伸展树。其中S1的所
有元素都小于S2的所有元素。
首先,我们找到伸展树S1 中最大的一个元素x,再通过Splay(x,S1)将x 调
整到伸展树S1 的根。然后再将S2 作为x 节点的右子树。这样,就得到了新的
伸展树S。如图所示
Split(x,S):以x 为界,将伸展树S 分离为两棵伸展树S1 和S2,其中S1
中所有元素都小于x,S2中的所有元素都大于x。
首先执行Find(x,S),将元素x 调整为伸展树的根节点,则x 的左子树就是
S1,而右子树为S2。如图所示

Code:
#include