【机器学习基础】乡村F4带你入门线性回归 带python代码示例(一)
标注:
1.概率密度没有学好,所以涉及到密度函数部分会有不少地方感觉非常难懂吃力
如何理解回归?
个人理解:回归是指 量化 {变量} 之间“关系”
线性回归的英文regression towards the mean。mean在英文中是平均值的意思。
求平均值通常是我们面对大量数据时,快速建立对数据的概念的方式。
比如:
- 1.中国人均生育1.3个孩子(被动养孩万岁)
- 北京人均餐饮消费40元(一单外卖吃40,坑爹)
- 智能手机均价2800元(此处由小米用户组成底部)
拿一组数据做分布图看
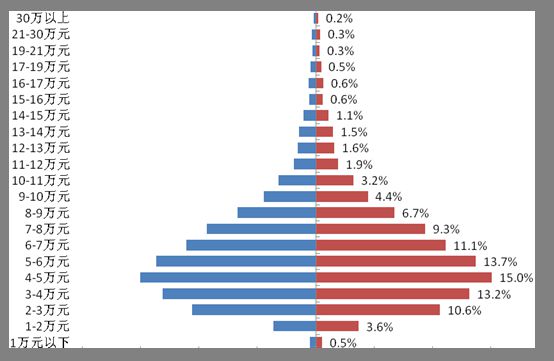
引用:北京市统计局 图:2017年北京市城镇居民收入层级分布对比图(城镇居民人均可支配收入)
图随便找的哈,只用看单边;我们可以估算出,北京城镇居民年人均可支配收入估计是在5-6万附近(帮忙算个平均数。。),我们也能大概估出来,随便找个工作,应该能在10712元。(老板听着头大)
那么,如何估算自己工资具体可以拿多少呢?
我们可以直接问老板(PIA!打脸)
Life is short,Show Me The Data!
没有数据说个毛啊
人生会不会像高考一样呢?语文+数学+英语+化学+物理+生物+政治+历史+地理 = 最终的成功人士排位呢?
很可惜,生活不只苟且,还有家庭背景、家庭背景、家庭背景等等的异常因素会影响你的排位。
但大城市的工资还是比较公平的,除了极个别的异常值,其他是可以进行预测的:
最低工资*θ0 × 公司类型*θ1 × 最高学历*θ2 × 学校排名*θ3 × 工作年限*θ4 × 长相*θ5 ≈ 工资
θ0~θ5为假设的参数,公司类型、最高学历等量化成数值,最低工资一般为一个莫(qian)须(gui)有(ze)的值,我们就直接用θ0代替
Y = x1*θ1 + x2*θ2 + x3*θ3 + x4*θ4 + x4*θ4 + x5*θ5 + θ0
那么我们来对身边的人做一些简单的调查
| 序号 | 姓名 | 性别 | 公司类型 | 最高学历 | 学校排名 | 工作年限(年) | 长相(分) | 工资(元) |
|---|---|---|---|---|---|---|---|---|
| 1 | 尼古拉斯•赵四 | 男 | 种花象牙山村村委理事会 | 1.小学 | 131429 | 1 | 2 | 200 |
| 2 | 亚历山大•小宝 | 男 | 巨硬科技有限公司 | 2.初中 | 64536 | 8 | 1 | 12,000 |
| 3 | 富兰克林•谢广坤 | 男 | 象牙山饭庄五部 | 2.初中 | 79080 | 12 | 7 | 18,000 |
| 4 | 克里斯蒂安•刘能 | 男 | 东北二人转技术学院 | 3.高中 | 26533 | 5 | 3 | 250 |
| 5 | 弗朗西斯•沈阳 | 无 | 美国加里敦大学 | 5.博士 | 9654 | 3 | 9 | 25,000 |
| 6 | 略 |
在anaconda环境下创建数据集
import pandas as pd
employ = {'序号':[1,2,3,4,5],
'姓名':['尼古拉斯•赵四','亚历山大•小宝','富兰克林•谢广坤','克里斯蒂安•刘能','弗朗西斯•沈阳'],
'性别':['男','男','男','男','无'],
'公司类型':['种花象牙山村村委理事会','巨硬科技有限公司','象牙山饭庄五部','东北二人转技术学院','美国加里敦大学'],
'最高学历':[1,2,2,3,5],
'学校排名':[131429,64536,79080,26533,9654],
'工作年限(年)':[1,8,12,5,3],
'长相(分)':[2,1,7,3,9],
'工资(元)':[200,12000,18000,250,25000]
}
df = pd.DataFrame(employ,columns=['序号','姓名','性别','公司类型','最高学历','学校排名','工作年限(年)','长相(分)','工资(元)']) #指定列名排序
df
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif']=['SimHei']
x = df['长相(分)']
y = df['工资(元)']
# 散点图
plt.scatter(x, # x轴数据为长相
y, # y轴数据为工资
s = 30, # 设置点的大小
c = 'black', # 设置点的颜色
marker = 'o', # 设置点的形状
alpha = 0.9, # 设置点的透明度
linewidths = 0.3, # 设置散点边界的粗细
label = '样本点'
)
# 建模
reg = LinearRegression().fit(x.values.reshape(-1,1), y)
# 回归预测值
pred = reg.predict(x.values.reshape(-1,1))
# 绘制回归线
plt.plot(x, pred, linewidth = 2, label = '拟合的回归线')
# 添加轴标签和标题
plt.title("长相跟工资的关系")
plt.xlabel("长相(分)")
plt.ylabel("工资(元)")
# 去除图边框的顶部刻度和右边刻度
# plt.tick_params(top = 'off', right = 'off')
# 显示图例
plt.legend(loc = 'upper left')
plt.show()
(因为多个维度无法用平面描述,所以就先做长相和工资的关系)
很明显长相和工资成正相关,但是不排除有异常值,‘亚历山大•小宝’颜值只有一分,但是却在巨硬工资当程序员,工资还是挺高的。
那么,这上面拟合的回归线是怎么拟合出来的呢?
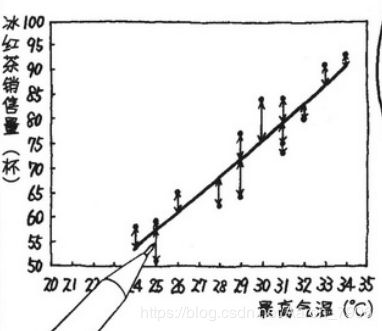
摘自:欧姆社学习漫画,统计学之回归分析
看图可以理解为求每一个点到直线的距离,当所有的点距离的和最小时,回归最优。(最小二乘法)
且这个只是两维表达方式。。。多维。。你看着办
然后如果是学统计学的同学,则需要回顾一下R方和假设检验,估计这个在时间序列预测中是挺重要的
当然这里省略掉了数学公式、对数最大似然估计和梯度下降
下一章我们来推公式