ML——回归模型（一）

目录

 

一、了解数据

二、探索性数据分析，了解变量分布与变量之间的关系

三、采用梯度下降法来求解回归系数

四、传入实际数据查看预测结果

使用梯度下降法实现简单的线性回归

一、了解数据

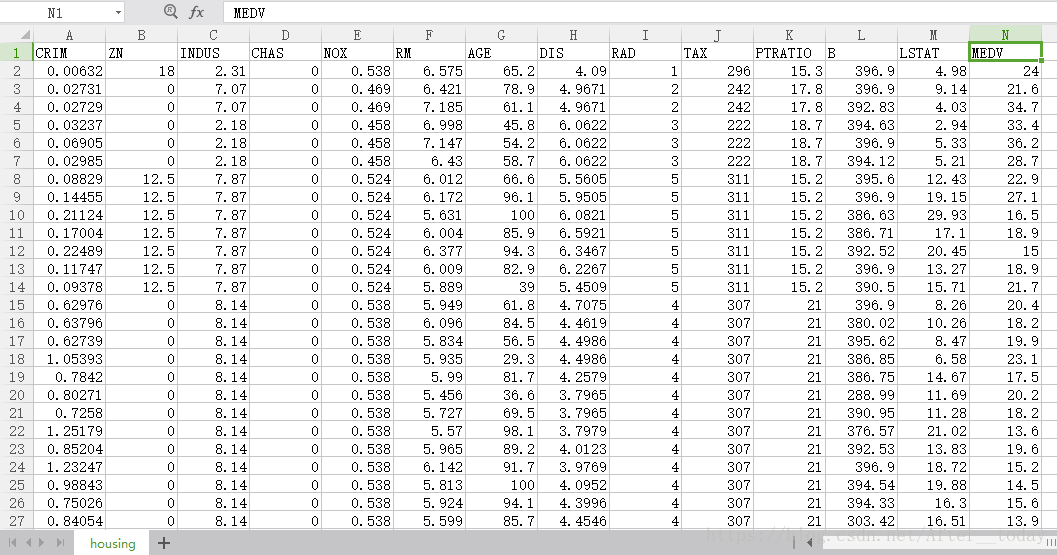
数据集：波士顿房价数据

预测变量与目标变量含义：

CRIM：每个城镇人均犯罪率
ZN：超过25000平方尺用地划为居住用地的百分比
INDUS：非零售商用地百分比
CHAS：是否被河道包围
NOX：氮氧化物浓度
RM：住宅平均房间数目
AGE：1940年前建成自用单位比例
DIS：5个波士顿就业服务中心的加权距离
RAD：无障碍径向高速公路指数
TAX：每万元物业税率
PTRATIO：小学师生比例
B：黑人比例指数
LSTAT：低层人口比例
MEDV：房价（预测变量）

二、探索性数据分析，了解变量分布与变量之间的关系

因为预测变量较多，这里选取四个预测变量其与目标变量(MEDV)之间的关系，这里我们先选择使用seaborn库的pairplot函数绘制数据集中的成对关系，此函数将创建一个Axes网格，使得每个变量将通过y轴在单个行和x轴上在单个列中共享，对角线上是变量分布的直方图（可修改），非对角线上是两个变量的散点图。

具体参数及其意义见官方文档http://seaborn.pydata.org/generated/seaborn.pairplot.html#seaborn.pairplot。

# 读入数据
import os
import pandas as pd

os.chdir('C:/Users/Administrator/Desktop/jpynb/机器学习')
df = pd.read_csv('./data/housing.csv')

# 绘制关系图
import matplotlib.pyplot as plt
import seaborn as sns

sns.set(style='whitegrid', context='notebook')  # 设定样式，还原可用sns.reset_orig()
# context绘制上下文参数，style轴样式参数
# 选取的四个预测变量及目标变量
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']

sns.pairplot(df[cols], size=3)
plt.tight_layout()
# tight_layout()是matplotlib的方法，紧凑显示图片，居中显示

# 存储图片
plt.savefig('C:/Users/Administrator/Desktop/scatter1.png', dpi=300)   # dpi是像素

从图中很容易看出RM和目标变量MEDV有一点正线性关系的感觉，接下来用更直观的相关系数来看看到底哪个（些）预测变量与MEDV相关性最强。

相关系数的数学公式：，cov是协方差，和是标准差，E是期望，numpy库中分别有cov()，std()，mean()来计算这些量，corrcoef()则是一步得到相关系数矩阵。代码中我们将变量的值做转置得到每个变量的行矩阵传给corrcoef()得到向量间的相关系数，然后以相关系数矩阵为data传给heatmap()函数画的最终的热点图。

import numpy as np
cm = np.corrcoef(df[cols].values.T)  # 计算相关系数
sns.set(font_scale=1.5)   # font_scale 单独的缩放因子，可以独立缩放字体元素的大小

# 画相关系数矩阵的热点图
hm = sns.heatmap(cm,   # 数据
        annot=True,    # annot为True时，在heatmap中每个方格写入数据
        square=True,   # 设置热力图矩阵小块形状，默认值是False 
        fmt='.2f',   # 矩阵上标识数字的数据格式
        annot_kws={'size': 11},   #annot为True时，可设置各个参数，包括大小，颜色，加粗，斜体字等
        yticklabels=cols,   #坐标轴标签名
        xticklabels=cols)
plt.tight_layout()
plt.savefig('C:/Users/Administrator/Desktop/corr_mat.png', dpi=300)

sns.reset_orig()   #还原seaborn样式设置

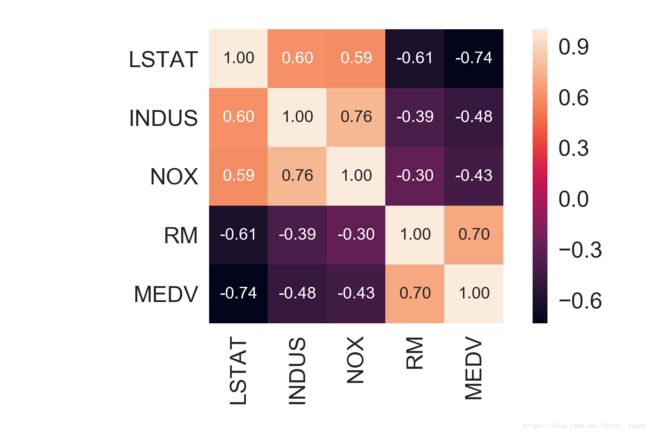
从热点图很明显看出相关性最强的是LSTAT(低层人口比例)和RM(住宅平均房间数目)，LSTAT与MEDV呈负相关关系，RM与MEDV呈正相关关系，选择用RM来做一下线性回归。

三、采用梯度下降法来求解回归系数

什么是回归系数呢，就是在回归方程中表示自变量x 对因变量y 影响大小的参数，放到梯度下降算法中，就是令代价函数最小的那个，这个是假设函数（回归方程）的斜率，关于梯度下降算法在我的另一篇笔记中有详细介绍：https://blog.csdn.net/After__today/article/details/81267788。

# 梯度下降算法的类
class LinearRegressionGD(object):
    def __init__(self, eta=0.001, n_iter=20):
        self.eta = eta  # learning rate 学习速率
        self.n_iter = n_iter  # 迭代次数

    def fit(self, X, y):  # 训练函数
        self.coef_ = np.zeros(shape=(1, X.shape[1]))  # 代表被训练的系数，初始化为 0
        self.intercept_ = np.zeros(1)
        self.cost_ = []   # 用于保存损失的空list

        for i in range(self.n_iter):
            output = self.net_input(X)  # 计算预测的Y
            errors = y - output
            self.coef_ += self.eta * np.dot(errors.T, X)
            self.intercept_ += self.eta * errors.sum()
            cost = (errors**2).sum() / 2.0   # 计算损失
            self.cost_.append(cost)   # 记录损失函数的值
        return self

    def net_input(self, X):   # 给定系数和X计算预测的Y
        return np.dot(X, self.coef_.T) + self.intercept_   # dot矩阵乘法

    def predict(self, X):
        return self.net_input(X)

# 导入RM和MEDV的数据
X = df[['RM']].values
y = df[['MEDV']].values

from sklearn.preprocessing import StandardScaler
# 标准化数据，保证每个维度的特征数据方差为1，均值为0，使得预测结果不会被某些维度过大的特征值而主导
# 归一化（标准化
sc_x = StandardScaler()
sc_y = StandardScaler()
# fit_transform()先拟合数据，然后转化它将其转化为标准形式
X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y)

lr = LinearRegressionGD()
lr.fit(X_std, y_std)  # 喂入数据进行训练

首先理解下这个类（对应着我另一篇博客的梯度下降的公式来看），eta学习速率（即），n_iter迭代次数（梯度下降的次数），errors误差（即代价函数中的），coef_梯度（即假设函数中的，假设函数的斜率），intercept_常数项（即假设函数中的，假设函数的截距），cost代价函数值，cost_总代价集合。中间关于代价函数的计算用到了一个小技巧。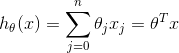

fit()函数是训练函数，根据上一次迭代计算的和同时更新和，然后计算代价函数cost；net_input()函数就是假设函数；predict()函数是预测函数，模型训练完毕之后调用这个对象传入自变量，预测因变量。

传入数据之前对数据做归一化处理，使得数据更为平滑，让梯度下降收敛所需要的循环次数更少，预测结果不会被某些维度过大的特征值而主导，具体的优化见https://blog.csdn.net/After__today/article/details/81329038。

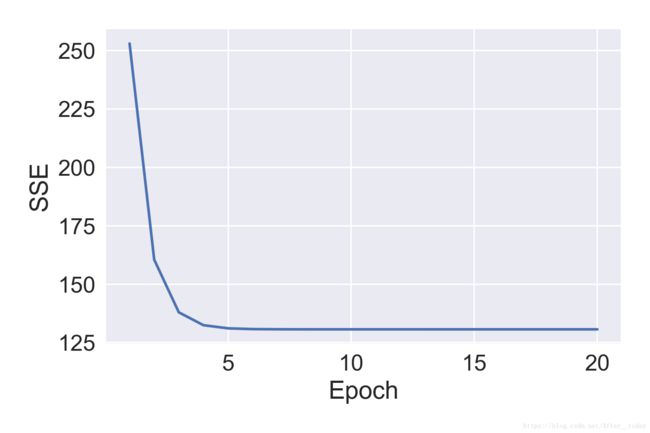
画出代价函数的图像看看训练效果：

plt.plot(range(1, lr.n_iter+1), lr.cost_)
plt.ylabel('SSE')   # 代价函数值
plt.xlabel('Epoch')   # 迭代次数
plt.tight_layout()

可以看出在下降大约5次之后代价就基本不再变化了（达到了最小化代价函数的目的）。画出预测的假设函数看看拟合的效果：

# 定义一个绘图函数
def lin_regplot(X, y, model):
    plt.scatter(X, y, c='lightblue')
    plt.plot(X, model.predict(X), color='red', linewidth=2)    
    return None

lin_regplot(X_std, y_std, lr)
plt.xlabel('[RM](standardized)')
plt.ylabel('[MEDV](standardized)')
plt.tight_layout()

四、传入实际数据查看预测结果

传入一个RM，看看预测的房价：

# 预测RM为10的时候房价为几多
num_rooms_std = sc_x.transform([[10.0]]) 
price_std = lr.predict(num_rooms_std)
print("预测房价为: %.3f" % sc_y.inverse_transform(price_std))

简单的线性回归实现基本就是这样。完整代码见：https://github.com/After-today/Regression。