ML——回归模型（二）

利用scikit-learn做线性回归

沿用上次房价数据中的RM(房间数)和MEDV(房价)，使用scikit-learn库中的LinearRegression()来做线性回归。

import os
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler

os.chdir('C:/Users/Administrator/Desktop/jpynb/机器学习')
df = pd.read_csv('./data/housing.csv')
df.head()

X = df[['RM']].values
y = df[['MEDV']].values

sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y)

slr = LinearRegression()
slr.fit(X_std, y_std)
print('Slope: %.3f' % slr.coef_[0])
print('Intercept: %.3f' % slr.intercept_)

def lin_regplot(X, y, model):
    plt.scatter(X, y, c='lightblue')
    plt.plot(X, model.predict(X), color='red', linewidth=2)    
    return None

lin_regplot(X_std, y_std, slr)
plt.xlabel('[RM] (standardized)')
plt.ylabel('[MEDV] (standardized)')
plt.tight_layout()

看一下图像效果，发现和使用梯度下降法拟合得到的图像相近：

使用RANSAC拟合稳健回归

首先理解下什么是稳健回归，在我们使用梯度下降法的时候会发现有很多异常点，当异常点数目较多时将会影响拟合的效果，这时候采用稳健回归来代替梯度下降算法。

再来看下RANSAC算法，算法步骤是：1、先从数据中随机选取模型设置的最小样本数的数据作为inliers；2、根据这些inliers计算适合的模型；3、在模型设置的残差范围内，将第一步没选到的数据带入模型，计算是否为inliers，并记下为inliers的数量；4、重复以上步骤，比较每次计算中的inliers数量，多的那次所建立的模型就是我们要的回归模型。

from sklearn.linear_model import RANSACRegressor
ransac = RANSACRegressor(LinearRegression(), 
                         max_trials=100, # 最大迭代次数
                         min_samples=50, # 从原始数据中随机选择的最小样本数
                         loss='absolute_loss', # 支持字符串“absolute_loss”和“squared_loss”，分别找出每个样本的绝对损失和平方损失。
                         residual_threshold=5.0, # 数据样本的最大残差，在这之内为内点
                         random_state=0)  #初始化中心的生成器
#  所有绝对残差小于残差阈值（residual_threshold）的数据样本都被认为是内点。
ransac.fit(X, y)

# 分出 inlier 和 outlier
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)

line_X = np.arange(3, 10, 1)  # 待预测的自变量
line_y_ransac = ransac.predict(line_X[:, np.newaxis])  # 预测因变量

plt.scatter(X[inlier_mask], y[inlier_mask], c='blue', marker='o', label='Inliers')
plt.scatter(X[outlier_mask], y[outlier_mask], c='lightgreen', marker='s', label='Outliers')
plt.plot(line_X, line_y_ransac, color='red')   
plt.xlabel('[RM]')
plt.ylabel('[MEDV]')
plt.legend(loc='upper left')  # 图例位于左上
plt.tight_layout()

看一下拟合结果：

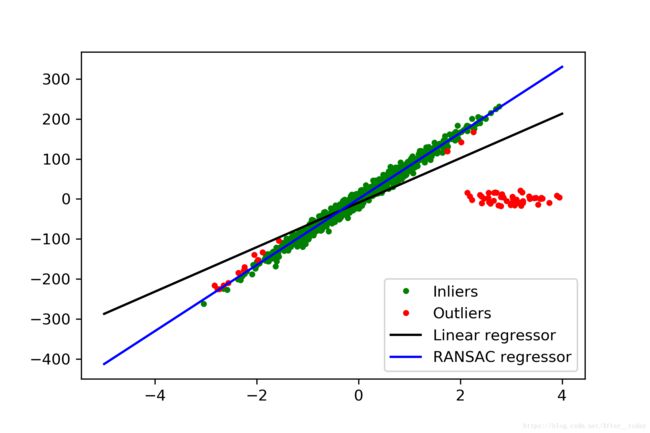
拿一组数据来看看简单线性回归和稳健回归的差异吧：

# datasets可以很好的帮助我们创造一组数据来实验
from sklearn import datasets

n_samples = 1000  # 样本数
n_outliers = 50  # 外点数

X, y, coef = datasets.make_regression(n_samples=n_samples, n_features=1,
                                      n_informative=1, noise=10,
                                      coef=True, random_state=0)
# n_features：特征数(自变量个数)
# n_informative：相关特征(相关自变量个数)即参与了建模型的特征数

# 添加 outlier 数据
np.random.seed(0)
X[:n_outliers] = 3 + 0.5 * np.random.normal(size=(n_outliers, 1))
y[:n_outliers] = -3 + 10 * np.random.normal(size=n_outliers)

# 使用所有数据进行简单线性拟合
model = LinearRegression()
model.fit(X, y)

# 利用RANSAC算法进行拟合
model_ransac = RANSACRegressor(LinearRegression())
model_ransac.fit(X, y)
inlier_mask = model_ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)

# 预测数据
line_X = np.arange(-5, 5)
line_y = model.predict(line_X[:, np.newaxis])
line_y_ransac = model_ransac.predict(line_X[:, np.newaxis])

# 对比预估的系数
print("Estimated coefficients (true, normal, RANSAC):")
print(coef, model.coef_, model_ransac.estimator_.coef_)

# 所有的样本点
plt.plot(X[inlier_mask], y[inlier_mask], '.g', label='Inliers')
plt.plot(X[outlier_mask], y[outlier_mask], '.r', label='Outliers')
# 两种拟合得到的回归模型
plt.plot(line_X, line_y, '-k', label='Linear regressor')
plt.plot(line_X, line_y_ransac, '-b', label='RANSAC regressor')
plt.legend(loc='lower right')

对比的结果很明显，RANSAC回归的效果要明显好于OLS 回归：

完整代码见https://github.com/After-today/Regression。