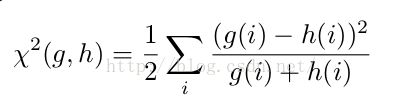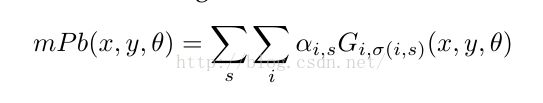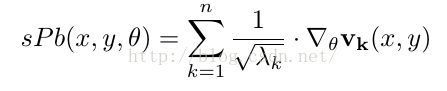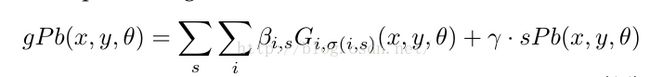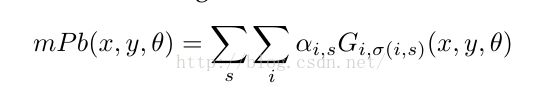Contour Detection and Hierarchical Image Segmentation 伯克利的一篇图像分割论文理解与学习

Contour Detection and Hierarchical Image Segmentation笔记

 

算法路线：gPb-------OWT------UCM

每一部份的功能：

1. gPb（global Pb）计算每一个pixel的作为boundary的可能性，即pixel的weight；

2. OWT（Oriented Watershed Transform）将上述gPb的结果转换为多个闭合的regions；

3. UCM（Ultrametric Contour Map）将上述regions集，转换为hierarchical tree；

 

 

●gPb：

gPb分为两个部分，分别为mPb和sPb

 

1. mPb：

Step1：

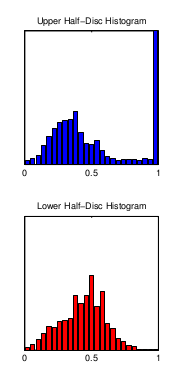
其思路是对于每一个pixel，以其为圆心，做出一个圆形。

用倾斜角为θ的直径，将圆形划分为两个区域，对于每一个区域中的pixels，做出它们的histogram，如下：

使用histogram数据，代入到距离公式：

该值，就是G（x，y，θ），代表pixel（x，y）以θ为方向的gradient magnitude；

 

Step2：

下一步，普通的Pb算法将每一幅图片，分解为4个不同的feature channels，分别是brightness, color a, color b以及texture channel，其中前三个channels是基于CIE color space。

而每个pixel的weight就是由这4个channels下计算得到的G(x,y,θ)值的加权和得到。

针对普通的Pb算法，作者提出了multiscale的方法，即为mPb。

它的原理是在原有Pb算法的基础之上，同时使用多个圆形直径长度δ（作者使用三个，[ δ/2 ,δ, 2δ]），针对每一个δ，计算其G（x，y，θ），最终公式如下：

 

公式中的i代表channel，s代表scale，意思是

对于每一个pixel，我们计算其每一个不同直径条件下的每一个feature channel的和，作为其mPb值；

α代表每一个不同直径条件下的每一个feature channel的权重，是针对F-measure进行gradient ascent得到，使用的训练集是BSDS。

 

2. sPb：

接下来计算sPb值。

首先，作者作出了一个sparse symmetric affinity matrix W，其中，每一个元素Wij的计算如下：

 

i，j代表两个距离不超过半径r（单位：像素，作者在代码中设定r=5）的像素，p是两个像素连成的线段上的任意一个点，找到某两个pixel连成的线段上的pixel的weight的最大值。ρ是常数，作者代码中设定为ρ= 0.1。

因为该矩阵W代表pixels之间的相似度，通过令得到矩阵D，由

 

计算得到前n+1个特征向量，代码中作者使用的是n=16；

 

接着，作者将每一个特征向量视为一幅图片，使用Gaussian directional derivative filters对它进行卷积操作，得到

 

 

从而，得到以下公式：

 

其中的参数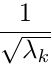是将特征向量的物理解释问题视为mass-spring system得到的。

自此，我们得到了mPb和sPb，总公式为：

 

β参数前面前文已经解释，参数γ是使用BSDS训练集，通过在F-measure =上进行gradient ascent得到。

最后，对于该gPb值进行sigmoid函数变换，使其值处于0-1之间，作为该pixel作为boundary的probability，我在下文都将其称为pixel的weight。

●OWT（Oriented Watershed Transform）：

对于每一个pixel，，（该E(x,y,θ)即为gPb公式）代入八个设定的角度θ∈[0, pi]，取其最大值；这样，每一个pixel均赋予了一个0到1之间的值，其值大小代表该pixel是boundary的可能性；

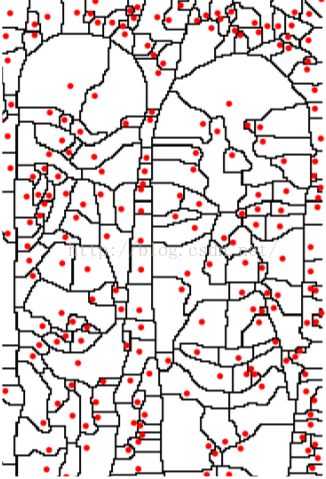
接着使用WT( watershed transform )技术，将以上的输入转化为一系列Po（regions）和Ko（arcs）。如图：

 

图中红点为其region的minimal，arcs即为边界。

原来的WT算法，是使用该arc上的pixels的weight的平均值作为其强度。

然而这种方法，会导致一些弱arc的某些pixel因为处在强arc的周边，在计算的过程中，选择了针对强arc的方向θ，从而该pixel的值偏大，于是弱arc的强度也相应偏大。如下图（两个石头像的中间，有许多横的强arc，这就是因为旁边的高强度的arc对它们的影响）：

 

而作者提出的OWT，是在WT的基础上，对所有处在arc上的pixel，重新选择合理的方向θ，计算E（x, y, θ），从而对arc的强度值作调整，方法如下：

 

 

 

对于每一个arc，我们将arc subdivide为许多线段，如图：

 

计算出其线段的方向，使用o（x，y）表示其方向，对于每一个pixel，重新计算其gPb，使用以下公式：

 

 

最后重新计算每个arc的强度，即为arc上所有pixels的weight的平均值，OWT步骤自此完成，对比效果如图（中间的横线的强度恢复正常）：

  

 

 

 

 

●UCM（Ultrametric Contour Map）：

为了在不同细节层次上对图像进行segmentation，作者使用了Ultrametric Contour Map (UCM)。

OWT算法已经output出细节度最高的regions集合，接下来，作者作出一个graph，如下：

 

其中，Po是regions，Ko是arcs，W(Ko)是该arc的强度。该图以region作为node，若两region相邻，则其对应的两个node相连，连接强度为W(Ko);

下一步，设两两regions之间的dissimilarity为其共同arc的强度平均值。

使用一种基于graph的merging技术，以两两regions之间的dissimilarity作为衡量标准，将regions按照dissimilarity升序排列，依次将dissimilarity小的region合并，直到最后只有一个region，这样，就完成了hierarchical tree的建设。

在这颗树中，因为生成树的每一个步骤，都是去除dissimilarity最小的arc，从而将两个region合并，因此，树中某个region元素的高度就代表着合并得到该region时，去除的arc的强度值大小，即：

 

因此，可以得到一个矩阵：

 

该矩阵的元素代表细节度最高的segmentation下，所有regions两两之间的dissimilarity，其值由两region的最小公共所属region的高度决定。

元素值计算公式如下：

 

 

由于该树符合以下性质：

 

因此，这是一个Ultrametric Contour Map (UCM)

由此，通过设定不同的阈值k，我们可以得到不同细节度的segmentation。

设定不同K值，代码运行结果如图：

原图：

 

 

 

k=0.0001                                                                                        k=0.001

                    

 

 

 

 

 

 

 

K=0.01                                                                                      K=0.05

                

 

 

 

 

K=0.1                                                                             K=0.12

 

 

K=0.5                                                                             K=0.9              

     

 

 

总结：

作者在原有的方法上，主要做了这四个方面的革新：

1. 在contour detector部分中的mPb环节引入了multiscale的概念，提出了mPb算法，可以将其视作普通Pb算法的加强版，公式如下：

 

2. 在contour detector部分中的sPb环节，对特征向量采取Gaussian directional derivative filters卷积操作，公式如下：

 

3. 提出了OWT（Oriented Watershed Transform），对原来算法中受强boundary影响而存在问题的pixel，结合其所属arc的方向再次计算其weight。

4. 将OWT生成的region集合组合成UCM（Ultrametric Contour Map），使得我们可以通过阈值k来输出不同细节度的图像轮廓。