详解RankNet原理及实践

0.pair-wise rank简介

         pair-wise rank的主要思想是把排序形式化为成对分类（pairwise classification）或成对回归（pairwise regression）问题。和point-wise 最大的区别是，pair-wise的样本是有一对item的相对关系组成的。例如对于某个用户u, 物品i比j更相关（用户u对i更感兴趣），则样本为（u,i,j) ，i>j ,label为正。具体到一条训练样本会包含u,i,j 的特征及label。然后采用分类算法训练分类模型。 预测时，只需要对所有pair进行分类，便可以得到文档集的一个偏序关系，从而实现排序。pair-wise rank 考虑文档对之间的偏序关系,更接近排序问题的实质。

         目前主要的pair-wise rank算法主要有：Ranking SVM[1], IR SVM[2]，GBRank[3], RankNet[4], LambdaRank[5]。不同算法的主要区别主要体现在损失函数不一样。

1.损失函数如何定义

      RankNet的核心是提出了一种概率损失函数来学习Ranking Function。
      对于一个排序，RankNet从各个doc的相对关系来评价排序结果的好坏，排序的效果越好，那么有错误相对关系的pair就越少。所谓错误的相对关系即如果根据模型输出Ui排在Uj前面，但真实label为Ui的相关性小于Uj，那么就记一个错误pair，RankNet本质上就是以错误的pair最少为优化目标。而在抽象成cost function时，RankNet实际上是引入了概率的思想：不是直接判断Ui排在Uj前面，而是说Ui以一定的概率Pij排在Uj前面，即是以预测概率与真实概率的差距最小作为优化目标。最后，RankNet使用Cross Entropy作为cost function，来衡量真实概率和预测概率Pij 之间的拟合程度：
                           （1）
其中，真实概率为：
（2）
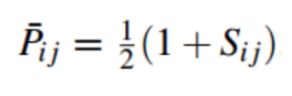
其中Sij ∈[1,0, -1]。 当sij = 1时， ${\overline{p}}_{i,j}$= 1，表示i排j前面，sij=0, ${\overline{p}}_{i,j}$=0.5,表示i,j前后怎么排都可以。。

预测概率定义:
（3）
oij = si - sj , 其中si = f(i) ,既学习的模型函数。将（2），（3）带入（1）：

RankNet算法的一大好处：使用的是交叉熵作为损失函数，它求导方便，适合梯度下降法的框架；而且，即使两个不相关的文档的得分相同时，C也不为零（log2），还是会有惩罚项的。

RankNet采用的模型为神经网络，这也是它称之为RankNet的原因。RankNet采用三层神经网络，一个单一的输出节点：

采用反向传播算法（等价随机梯度下降）来学习模型的参数。具体的学习过程，可以参考参考文献【6】

这里为了更好的理解，稍微对损失函数，优化函数，模型（f(x)) 说明一下。对于一个机器学习问题，首选我们要选择采用怎样的模型，这个模型通常会有一个形式化的定义，比如逻辑回归，模型就是logisic函数，神经网络，模型为类似上面的函数等。这个是最终要得到的模型的数学表示。后面预测的时候的输入就是该函数的输入。 有了这样的模型定义，最开始，对于它的参数我们是不知道的，这个时候机器就要负责去学习到这些参数（这就是机器学习呀^_）。怎么学习？ 已知了一些样本（模型函数的输入和输出），我们希望将样本输入（特征值）输入到模型后得到的输出，能和真实的输出越匹配越好。这个时候就要定义损失函数来衡量预测结果和真实结果的匹配程度。然后最小化它（以及加上一些类似正则化的处理），就是优化函数。

3.如何实现

关于RankNet的实现，paddlepaddle 有提供具体的调研方法。大家可以参考：https://github.com/PaddlePaddle/models/tree/develop/legacy/ltr

参考：
【1】Ralf Herbrich, Thore Graepel, and Klaus Obermayer. Support vector learning for ordinal regression. May 20 1999. DOI: 10.1049/cp:19991091 37, 40

【2】Yunbo Cao, Jun Xu, Tie-Yan Liu, Hang Li, Yalou Huang, and Hsiao-Wuen Hon. Adapting ranking SVM to document retrieval. In SIGIR’ 06, pages 186–193, 2006. DOI: 10.1145/1148170.1148205 22, 25, 37, 44

【3】Zhaohui Zheng, Hongyuan Zha, Tong Zhang, Olivier Chapelle, Keke Chen, and Gordon Sun. A general boosting method and its application to learning ranking functions for web search. In J.C. Platt, D. Koller, Y. Singer, and S. Roweis, editors, Advances in Neural Information Processing Systems 20, pages 1697–1704. MIT Press, Cambridge, MA, 2008. 22, 26, 37, 47

【4】ChrisBurges,TalShaked,ErinRenshaw,AriLazier,MattDeeds,NicoleHamilton,andGreg Hullender. Learning to rank using gradient descent. In ICML ’05: Proceedings of the 22nd inter- national conference on Machine learning, pages 89–96, 2005. DOI: 10.1145/1102351.1102363 22, 25, 37, 49

【5】C.J.C. Burges, R. Ragno, and Q.V. Le. Learning to rank with nonsmooth cost functions. In Advances in Neural Information Processing Systems 18, pages 395–402. MIT Press, Cambridge, MA, 2006. 22, 26, 37, 52, 53
【6】Li Hang, Learning to Rank for Information Retrieval and Natural Language Processing