k-svd实现人脸缺失像素补全
问题描述
数据集为来自YaleB的格式为pgm的分辨率为192 * 168的38张完整人脸图像。
使用K-SVD算法实现人脸图像的像素缺失填补实验,实验包括:
(1)使用YaleB数据集中的部分人脸图像,根据ksvd算法得到字典;
(2)对未参与字典训练的人脸图像进行50%,70%像素点缺失处理;
(3)使用字典填补(2)得到的像素缺失图像。
(4)分别进行不同次数的迭代并比较结果。
解决分析
选用的稀疏优化方法是OMP,且OMP自己用python实现了一回,但还是sklearn的Orthogonal Matching Pursuit更快些
算法描述
OMP
以贪婪迭代的方法选择D的列,使得在每次迭代的过程中所选择的列与当前冗余向量最大程度的相关,从原始信号向量中减去相关部分并反复迭代,只到迭代次数达到稀疏度K,停止迭代[1]。伪代码如下[2]:

进一步为了提高速度,可以用batch-OMP[3]实现OMP
K-SVD
K-SVD算法的思想是不断更新字典,使得字典,主要包括:
1.初始化字典;
2.稀疏编码(OMP或BP算法);
3.更新字典(通过SVD逐列更新)。
K-SVD实现注意:
信号集Y和字典D在计算前要归一化。字典的初始方法很多,此处选用了随机初始化。归一化采用了L2-norm。
ImageReconstruct:
实现逻辑:
用训练得到的D以及受损的信号集Y_loss,通过OMP解得表达X,再用D·X重新表示信号,即实现了受损图像的恢复。
实现注意:
1.在投入OMP前要归一化,保留信息
2.图像在转成uint8前先取绝对值,去过界值
实验数据处理
将数据集分为训练集和测试集,21张为训练集,17张为测试集。设置四次实验。第一,二次实验,给测试集图像加50%的椒盐噪声,K-SVD迭代次数分别设置为5,100。第三,四次实验,给测试集图像加70%的椒盐噪声,K-SVD迭代次数分别设置为5,100。
1.对训练集的预处理
先将训练集中的每一张图像分为504个88的分片,共得到21504个分片,从中抽取小于等于504个分片,将分片以64*1的列向量的形式相并,得到训练信号。
初始字典采取随机生成的形式。
对上述生成的训练信号及字典用L2范式归一化。
通过K-SVD训练得到字典D。
2.对测试集的预处理
用50%/70%/90%的椒盐噪声生成缺失图像
重构缺失图像
将缺失图像分为8*8的原子,纵向合并,L2范式归一化,得到测试信号Y’;
用OMP算法得到该图像的表示X;
再用D*X作为对Y’的复原;
将Y’展开,伸展范围为原范围,得到修复完善的图像。
实验结果及实验分析
结果展示
下面将展示50%、70%、90%损失比例下的恢复效果(30次迭代)。
90% loss & Reconstruct
直观看来,恢复效果并无显著差异,下面将做进一步分析。
实验分析
记录K-SVD每次迭代的误差。
记录每副恢复的图像的PSNR值。
PSNR[5](峰值信噪比)是一个表示信号最大可能功率和影响它的表示精度的破坏性杂讯功率的比值的工程术语。
本实验中,PSNR值用以下公式计算:
P S N R = 10 ∗ l o g 10 ( 255 ∗ 255 M S E 2 ) PSNR=10*log_{10}{(\frac {255*255}{MSE^2})} PSNR=10∗log10(MSE2255∗255)
M S E = 1 168 ∗ 192 ( L o s s − R e c ) 2 MSE = \frac {1}{168*192}{(Loss-Rec)}^2 MSE=168∗1921(Loss−Rec)2
误差图
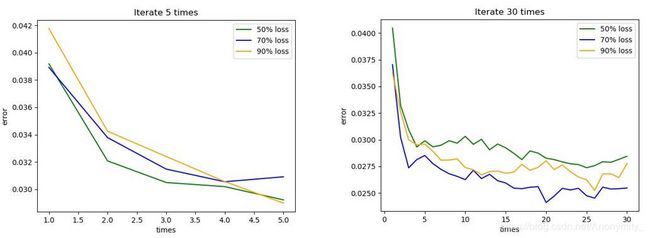
左图是k-svd迭代5次误差图,右图是迭代30次的。可以看出,5次迭代内,误差迅速降低,但5次以后,误差下降就变慢了,而且误差波动较大。而且图片的损失程度对字典表达的误差影响不太大。
PSNR
所取的PSNR值为17张测试集图像对应PSNR的均值。可以看出,损失比例的变化对恢复的效果影响不是很明显。
小结
1.通过复现k-svd算法和omp算法,实现人脸受损图像的恢复,加深了对字典学习的理解。
2.每组实验只进行了一次,在实验分析中所描述的现象并不具有代表性。
选用omp算法进行的稀疏表达,实现的omp是表达中的时间瓶颈,进一步可以尝试batch-omp算法优化时间(如sklearn所实现的omp)。
3.我是将图片切成8*8的像素块作为一列原子的,所以最后恢复得到的图片能明显看出像素块与像素块的差异,如果将像素块定义地更小,则恢复的图像或许会有更好的视觉效果。
总代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
import random
import cv2
import os
from scipy import sparse
np.set_printoptions(threshold=np.nan)
f = open('debug.txt','w',encoding='UTF-8')
def sep_img(img):
dim_r = img.shape[0] // 8
dim_c = img.shape[1] // 8
dim = dim_r * dim_c
patchs = np.zeros((64, dim))
for i in range(dim_r):
for j in range(dim_c):
r = i * 8
c = j * 8
patch = img[r:r+8,c:c+ 8].reshape(64)
patchs[:,i*dim_c + j] = patch
return patchs
def patch_merg(patchs, shp):
img = np.zeros(shp)
dim_r = img.shape[0] // 8
dim_c = img.shape[1] // 8
for i in range(dim_r):
for j in range(dim_c):
r = i * 8
c = j * 8
img[r:r+8,c:c+8] = patchs[:,i*dim_c+j].reshape(8,8)
return img
def miss_pic(img,k = 50):
patchs = sep_img(img)
k = int(k*0.01*patchs.shape[0]*patchs.shape[1])
loss_r = np.random.randint(0, high = patchs.shape[0]-1,size = k)
loss_c = np.random.randint(0, high = patchs.shape[1]-1,size = k)
for i in range(k):
patchs[loss_r[i],loss_c[i]] = 0
return patchs
def reconstruct(img, D, K):
patchs = sep_img(img)
# f.write(str(np.nonzero(patchs[:,17])[0]))
for i in range(patchs.shape[1]):
patch = patchs[:,i]
index = np.nonzero(patch)[0]
if index.shape[0] == 0:
continue
l2norm=np.linalg.norm(patch[index])
mean=np.sum(patch)/index.shape[0]
patch_norm=(patch-mean)/l2norm
# f.write("index:"+str(index.shape) + '\n')
# f.write("patch:"+str(patch_norm[index].T.shape) + '\n')
# print("reconstruct...OMP")
# x = cs_omp(patch_norm[index].T,D[index, :])
x = OMP(D[index, :], patch_norm[index].T, K)
# x = linear_model.orthogonal_mp(D[index, :], patch_norm[index].T,None)
# print("reconstruct...OMP DONE!!")
patchs[:, i]=np.fabs(((D.dot(x)*l2norm)+mean).reshape(patchs.shape[0]))
return patch_merg(patchs,img.shape)
def OMP(D,Y,T):
if len(D.shape) > 1:
K = D.shape[1]
else:
K = 1
D = D.reshape((D.shape[0],1))
if len(Y.shape) > 1:
N = Y.shape[1]
else:
N = 1
Y = Y.reshape((Y.shape[0],1))
X = np.zeros((K,N))
for i in range(N):
y = Y[:,i]
r = y
indx = []
for k in range(T):
proj = np.fabs(np.dot(D.T,r))
pos = np.argmax(proj)
indx.append(pos)
if k == 0:
A = D[:,pos].reshape(Y.shape[0],1)
else:
A = np.concatenate((A,D[:,pos].reshape(Y.shape[0],1)),axis = 1)
x = np.dot(np.linalg.pinv(A),y)
r = y - np.dot(A,x)
# f.write('y:'+str(y.shape)+"\n")
# f.write('A:'+str(A.shape)+"\n")
# f.write('x:'+str(x.shape)+"\n")
tmp = np.zeros((K,1))
tmp[indx] = x.reshape((T,1))
tmp = np.array(tmp).reshape(K)
X[:,i] = tmp
return X
def K_SVD(img,iter_times,K, T,err=1e-6): #T为OMP的迭代次数
Y = sep_img(img) # n * N n = 64 为原子维度, N = img.shape[0]*img.shape[1] // 64 为原子数
n = 64
N = Y.shape[1]
X = np.zeros((K,N))
#生成初始字典
D = np.random.random((n,K))
for i in range(K):
norm = np.linalg.norm(D[:,i])
mean=np.sum(D[:,i])/D.shape[0]
D[:, i] = (D[:, i]-mean) / norm
for i in range(N):
norm = np.linalg.norm(Y[:,i])
mean = np.sum(Y[:,i]) / Y.shape[0]
Y[:,i] = (Y[:,i] - mean) / norm
for j in range(iter_times):
# X = linear_model.orthogonal_mp(D, Y, None)
X = OMP(D,Y,T)
# X = cs_omp(Y,D)
e = np.linalg.norm(Y- np.dot(D, X))
f.write(str('%s' % e)+'\n')
print(str('第%s次迭代,误差为:%s' %(j, e))+'\n')
if e < err:
break
for k in range(K):
index = np.nonzero(X[k, :])[0]
if len(index) == 0:
continue
D[:, k] = 0
R = (Y - np.dot(D, X))[:, index]
u, s, v = np.linalg.svd(R, full_matrices=False)
D[:, k] = u[:, 0].T
X[k, index] = s[0] * v[0, :]
return D
def psnr(a,b):
if (a==b).all(): return 0
return 10*np.log10(a.shape[0]*a.shape[1]/(((a.astype(np.float)-b)**2).mean()))
dire = 'D:\\paperReading\\presentationLearning\\DataSet\\'
data = []
data_num = 0
for root,dir,files in os.walk(dire):
for file in files:
data.append(cv2.imread(dire + str(file),-1))
data_num += 1
ratio = 0.8 #训练集/测试集
randomnum = np.random.randint(0, high = data_num, size = int(ratio * data_num))
train_set = []
test_set = []
for i in range(data_num):
if i not in randomnum:
test_set.append(data[i])
else:
train_set.append(data[i])
N = 504
K = 256
T = 50
atoms = np.array(sep_img(train_set[0]))
for i in range(1,len(train_set)):
patchs = sep_img(train_set[i])
atoms = np.concatenate((atoms,patchs),axis = 1)
train = atoms[:,np.random.randint(0, high = atoms.shape[1]-1, size = N)]
D = K_SVD(train,30,K,T)
for i in range(len(test_set)):
loss = patch_merg(miss_pic(test_set[i],90),test_set[i].shape)
cv2.imwrite("D:\\paperReading\\presentationLearning\\LossPic\\loss"+str(i)+".jpg",loss.astype(np.uint8))
print("Loss "+str(i)+" has been loaded..")
rec_img = reconstruct(loss,D,K)
cv2.imwrite("D:\\paperReading\\presentationLearning\\RecPic\\rec"+str(i)+".jpg",rec_img.astype(np.uint8))
print("Loss "+str(i)+" is reconstructed!")
f.write(str('%s' % psnr(test_set[i],rec_img ))+'\n')
参考资料
[1]. http://blog.sciencenet.cn/blog-810210-653094.html
[2]. 基于压缩传感的匹配追踪重建算法研究 高睿
[3]. Efficient Implementation of the K-SVD Algorithm and the Batch-OMP Method Ron Rubinstein∗ , Michael Zibulevsky∗ and Michael Elad∗
[4]. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation Michal Aharon, Michael Elad, and Alfred Bruckstein
[5]. https://zh.wikipedia.org/zh-hans/峰值信噪比




