BP神经网络C++实现

      寒假在家做一点项目，这也是最后一块比较多的时间能做项目了，下学期主要投入时间考研，之所以写这篇文章是因为想记录一下自己的学习历程，若是能帮助到恰好需要帮助的人那是更好不过。

      因为我对Python不怎么了解，因此我选择用c++实现bp网络，虽然都说机器学习用得比较多的是Python。像很多人一样，我也是一边学编程一边做一些项目，之前做过adaboost人脸检测和pca的人脸识别，所以我实现这个神经网络主要是用来做人脸识别用的，那么废话不多说直接进入主题。

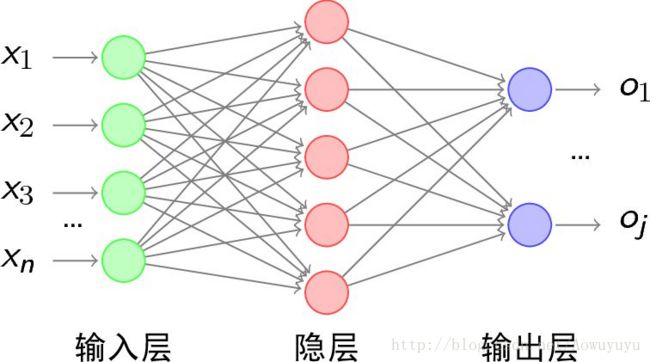
       首先要实现这个网络就要先对bp神经网络的算法有一定的了解，可以不需要了解那么透彻，反正能用代码将那些公式过程实现出来即可，编程的主要目的还是偏重于应用，解决实际问题。首先我们知道bp神经网络分为三个层：输入层，隐层，输出层。

大致结构如上图所示，它的主要工作机制就是：在输入层输入n个数，经过隐层和输出层的两次计算，最后在输出层能得到m个结果，你事先给定这m个结果分别是什么，神经网络通过它计算的结果和你希望它出来的结果进行误差计算，并返回调整权重值，经过一次又一次的计算，神经网络能输出的结果和你最终希望得到的结果会越来越接近。

      神经网络的理论知识我先扯到这里，接下来开始实践。用c++的话，我就选择了设计类来实现，类结构如下所示

class BPNet
{
	static double eta;
	vectornetwork;
public:
	BPNet();
	void set(const vector & network_);
	~BPNet();
	static double sig(double &x) { return 1.0 / (1.0 + exp(-x)); }
	void front(vector &input_, const vector & network_);
	void back_p(const vector & predict);
	void update_weight();
	void show() const;
}; 

私有成员包括学习率eta（这个有点类似步长的意思）这里将它用static修饰因为它属于神经网络类，还有一个vector数组代表“层”（这个层的结构我接下来会给出），再来看看方法：默认构造函数析构函数就不多说了，我这里定义了一个set用于初始化，然后一个前向传播函数一个反向传播函数再加一个权重更新函数就是主要的方法了，至于激活函数，它也属于类，因此也用static修饰，因为它比较短小而且使用次数比较多因此声明为内联函数。

struct neuron
{
	vectorweight;
	vectorupdate_w;
	double input;
	double output = 0;
	double bias;
};
typedef vectorlayer;

这是神经元结构，你可以这样想，一个大的神经网络有很多层组成，而每一层又由许多神经元组成，因此神经元是最小的单位，神经元里需要储存的数据有权重，输入，输出，偏置。这里用vector的原因是事先并不能确定个层需要几个神经元，用vector方便改变大小。类总体结构说得差不多了，接下来我们看看方法具体的实现吧

void BPNet::set(const vector & network_)
{
	int layer_num = network_.size();
	for (int i = 0; i < layer_num; i++)
	{
		network.push_back(layer());
		for (int j = 0; j < network_[i]; j++)
		{
			network.back().push_back(neuron());
			if (i > 0)
			{
				network[i][j].bias = 0.5;
			}
			if (i < layer_num - 1)
			{
				for (int k = 0; k < network_[i+1]; k++)
				{
					network[i][j].weight.push_back(rand()*(rand() % 2 ? 1 : -1)*1.0 / RAND_MAX);
					network[i][j].update_w.push_back(0);
				}
			}
		}
	}
}

首先是网络的初始化函数，初始化的部分主要包含以下几部分：网络层数（简单的一般就是三层），每层所含的神经元个数，每个神经元的初始权重和初始偏置。对于三层的网络而言，权重其实需要两组就够了，输入和隐层之间一组权重，隐层和输出之间一组权重，那么你的权重可以保存在输入层和隐层也可以保存在隐层和输出层，我采用的是前者，因为感觉运算方便一点。偏置的设置很简单，同一层的偏置是一样的，也是设置两层就好，权重的初始值都设为-1到 1之间的随机值就好。

void BPNet::front(vector &input_, const vector & network_)
{
	for (int t = 0; t < network_[0]; t++)
	{
		network[0][t].output = input_[t];
	}
	for (int i = 1; i < network_.size(); i++)
	{
		for (int j = 0; j < network_[i]; j++)
		{
			network[i][j].output = 0;
			for (int k = 0; k < network_[i-1]; k++)
			{
				network[i][j].output += network[i-1][k].output * network[i-1][k].weight[j];
			}
			network[i][j].output += network[i][j].bias;
			network[i][j].output = sig(network[i][j].output);
		}
	}
}

接下来我们来看一下前向传播函数，这个函数其实不难实现，输入层不用管，输入层的输出就等于你的输入值，主要是计算隐层和输出层。隐层的输出值应该是等于 ：（输入层的每个神经元的输出乘以对应的权重然后加上偏置）把这个整体放入激活函数 得到的值，输出层也是一样的，具体的可以看代码。最后输出层可以得到几个输出，那个就是整个神经元的输出。

void BPNet::back_p(const vector & predict, double & error)
{
	double delta_total = 0.0;
	double delta = 0.0;
	double sum;
	for (int i = 0; i < predict.size(); i++)
	{
		delta_total += 0.5*pow((predict[i] - network[2][i].output),2);
	}
	error = delta_total;
	//std::cout <<"total delta is "<< delta_total << std::endl;
	for (int i = 0; i < network[1].size(); i++)
	{
		for (int j = 0; j < network[2].size(); j++)
		{
			delta = -(predict[j] - network[2][j].output)*network[2][j].output*(1 - network[2][j].output)*network[1][i].output;
			network[1][i].update_w[j] = network[1][i].weight[j] - eta*delta;
		}
	}
	delta = 0.0;
	for (int i = 0; i < network[0].size(); i++)
	{
		for (int j = 0; j < network[1].size(); j++)
		{
			sum = 0.0;
			delta = network[1][j].output*(1 - network[1][j].output)*network[0][i].output;
			for (int k = 0; k < network[2].size(); k++)
			{
				sum += -(predict[k] - network[2][k].output)*network[2][k].output*(1 - network[2][k].output)*network[1][j].weight[k];
			}
			delta *= sum;
			network[0][i].update_w[j]=network[0][i].weight[j] - eta*delta;
		}
	}
}

这是反向误差函数，看起来有点复杂，因为里面涉及到了链式法则求导的问题，这块我也看了挺多便的，但其实看懂了就还好。首先要清楚一点反向传播函数的主要目的是为了修正权重，而且输出层和隐层的权重修正是不一样的，修正的公式就是w_update=w_old-eta*delta，关键是delta要求出来，这个delta是你要修正的那个权重对总误差求偏导数得到的值，单个误差就是（predict-out）的平方，也就是某个输出层神经元预期的输出和真实输出的差值的平方，总误差就是把它们加起来，对于输出层的神经元，权重只会影响到单个的输出，而对于隐层而言，一个权重的改变会对所有神经元的输出均有影响，具体公式这部分的内容有一个网站说的特别详细（yongyuan.name/blog/back-propagtion.html）我也是参考他的公式并自己总结出来编写了代码。
最后一部分比较简单，更新权重，要注意的是权重更新一定要等反向传播完成了以后再更新，因为在修正隐层权重的时候，需要用到输出层原来的那组权重，这个具体看那部分教程就明白了

void BPNet::update_weight()
{
	for (int i = 0; i < network.size() - 1; i++)
	{
		for (int j = 0; j < network[i].size(); j++)
		{
			network[i][j].weight = network[i][j].update_w;
		}
	}
}

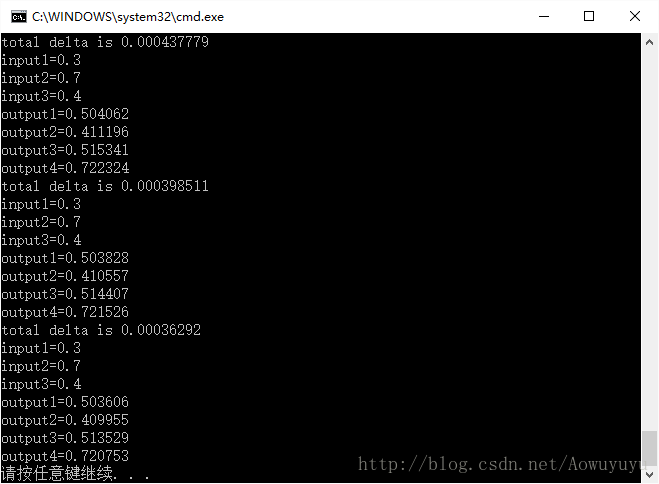
最后一个显示信息函数，没什么可说的，验证结果是否正确需要它

void BPNet::show() const
{
	for (int i = 0; i < network[0].size(); i++)
	{
		std::cout << "input" << i + 1 << "=" << network[0][i].output << std::endl;
	}
	for (int i = 0; i < network[2].size(); i++)
	{
		std::cout << "output" << i + 1 << "=" << network[2][i].output << std::endl;
	}
}

写一个小程序来测试它是否正确

#include
#include
#include"Net.h"
int main()
{
	BPNet bpnetwork;
	vectorly{ 3,3,4};
	vectorinput{ 0.3,0.7,0.4 };
	vectoroutput{0.5,0.4,0.5,0.7};
	bpnetwork.set(ly);
	for (int i = 0; i < 100; i++)
	{
		bpnetwork.front(input, ly);
		bpnetwork.back_p(output);
		bpnetwork.update_weight();
		bpnetwork.show();
	}
	return 0;
}

初始化了一个三输入四输出的网络输入值0.3,0.7,0.4，希望的输出值是0.5,0.4,0.5,0.7，都是随意设的，要注意输入可以随便设但输出只能是0-1之间，因为激活函数值域就是0-1，因此假如设置了大于1的数，它训练的结果肯定是无限接近于1。当然，这只是验证一下神经网络究竟能否工作，在真正的训练中，只有一个样本输入的神经网络是没有任何意义的，所以，要验证神经网络是否写成功了，还得需要进行实际的训练，我选择较为简单的手写数字识别作为实战项目先试一试，这部分若是有时间我也会写一个记录，在这个神经网络的完成过程中，我也参考了一些比较形象生动的资料，有些编程思路比较好的就化为自己的一部分内容，上要是有哪些描述不准确或者错误的地方欢迎各位指正！