数据结构之---树
这里说得树是基本的树结构,至于高级树结构我会慢慢更新上来的。
先说我们为什么要用树??? :如果有1000条数据,你想找到“s”在哪,如果在第999的位置呢?有人可能说那倒过来,那你倒过来他要是第一个呢??效率就很低吧?所以二叉树大部分的运行时间平均是O(logN),上面说的那种是O(N),O()为大欧记法,不明白请稍微了解下。想了解二叉树的效率还要了解下二分法查找。
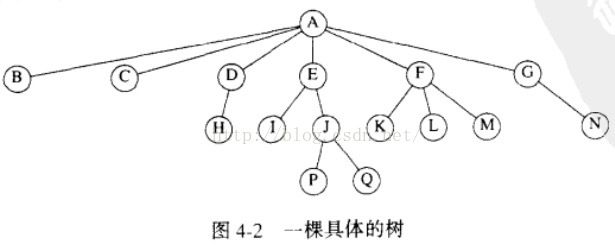
什么是树:把大树倒过来, 把它倒过来(你倒立也行)就是树状结构图。他得模样就是树,树根就是根节点(父亲),树梢就是边,树梢的每一个拐弯处就是子节点(儿子),有多少层就叫深度。那么图4-2从A到Q。深度就为4。
这货就是一颗一般的树了,,, 为什么要用一般。。 因为还有很多特殊的树(B树,avl,红黑等等)。
那么什么叫二叉树??顾名思义!最多两个树叉子,如下图每个节点最多只有两个节点就叫二叉树(听起来像脏话2X。。)。
你以为这就完啦?? 哈哈哈哈!!天真,还有完全二叉树跟满二叉树
满二叉树就是“丰满”的二叉树。 那就是所有子节点没有缺失的二叉树。看起来很丰满(根节点1个,二层子节点2个。三层4个,四层8个。。。)
那么完全二叉树怎么回事? 在二叉树的基础上,把最最最下面的子节点的右边删了就叫完全二叉树(删除几个都行,全部都干掉包括左边的也行。但是必须挨个删除,不能跳着删)。这样的话就变成残疾了不是么??所以大家可以理解为(从右脚开始残疾的二叉树,也许俩脚都残疾了)。
注意:有很多树形结构,但是你要从基础开始后续的高级结构都是初级结构的变体。
记忆比喻:这么形象。。。就是树。。
树怎么存?:我们都知道物理结构上只有表跟链。物理结构是没有树跟图结构的,那只能吧他转成表结构去存储了,顺序存储只适用于满二叉树,完全二叉树。如一图4-2如果用数组来存,先吧空元素填满。因为数组是连续的内存,不填空得话怎么确保下一个元素在准确的位置,然后从上到下从左到右的存。顺序是1-2-3-4...i,第i个位置的下标就是i-1。这样就很浪费内存,因为有很多空。
链式存储:因为链有双指针域(指针地址),一个指向左孩子,一个指右孩子。第二种是,可以增加一个指针域存储他得父母。还有上一个兄弟/下一个父母方式,按照下图的箭头存储,一个存上一个兄弟一个存下一个孩子。这样可以吧任意一个树转换成二叉树。
这样我们是不是吧一棵树转成二叉树了呢,为什么要用二叉树,因为他拥有很多特性。还有很多比较方便的算法。
操作方式
树结构都是递归的分为三种,如下图顺序
先根遍历:先访问根节点然后遍历左子树,最后遍历右子树。先遍历跟节点-然后是以+为根节点的子树+然后是a然后是右子树X然后是b..形成- +a*b-cd/ef
中根遍历:中序遍历左子树,访问根节点,最有中序右子树。先遍历左子树a然后以+为根节点的根+,遍历以X为根节点的左子树b..形成 a+b*c-d - e/f
后根遍历:后序遍历左子树,后序右子树,最后访问根节点。先遍历左子树a然后以X为根节点的左子树b,然后是C和D,访问跟节点-,然后x,+形成 abcd-*+ef/ -
上面加大得字体就是代码实现的递归顺序,下面是递归代码。
Status PreOrderTraverse(BiTree T,Status(* Visit)(TElem Type)){
if(T){
Visit(T->data) //根节点
PreOrderTraverse(T->lchild,Visit) //左孩子
PreOrderTraverse(T->rchild,Visit); //右孩子
}
else return OK;
}
接下来是线索二叉树:他就非常简单,地址域变成4个就可以了,分别存储做孩子右孩子和左孩子右孩子的线索,比如是否为空还是存在,为左右存储节点提供线索。
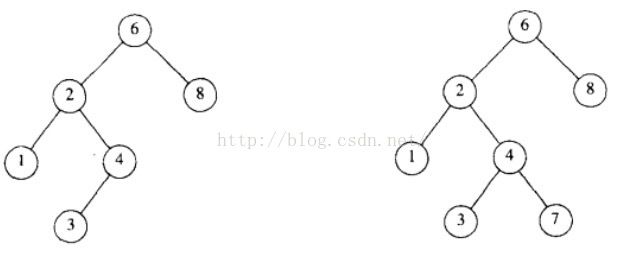
二叉查找树/二叉搜索树,这个是最适合搜索的树类结构之一,以根节点为中心,左边的子树集合永远比根节点小,右边的子树集合永远比根节点大,下图只有左边的是二叉查找树。因为根为6那左边的图的左节点是没有比6大得。但右图的最后有一个左侧的根节点为7大于6,所以他就不是二叉查找树,7改成5二叉查找树依然成立。
如上图结构要查找key(数字只是key,并不是实际值)就相当容易。平均深度为O(logN)。
创建一棵树:
MakeEmpty(SearchTree T){
if(T != NULL){
MakeEmpty(T->Left) //先建立左树
MakeEmpty(T->Right); //右树
free(T);
}
return NULL;
}查找就相对简单,跟结构规则一样的。如果比要查找的X大就往左节点查找,小就右节点
Find(ElementType X,SearchTree T){
if(T == null){
return null;
if(XElement)
return Find(X,T->Left); //X大于T元素,左查找递归
else
if(X> T->Element) //如果X大于T元素,右查找递归 else return T;
}}
那么如何查找最大跟最小的???:如上图查找,如果左节点的下一个元素为空,那他就是最后一个元素,我们根据二叉查找树的规则可以判断,那就是最小的,最大的就是最右边为空的元素。
插入也是按照规则,如果比他大就插入右边,相反就左边。
删除是最麻烦的,首先要判断如果他没有子元素就可以直接删除。那么如果他有子元素怎么办。特别是左右都有孩子怎么办?
如果他有单个子元素:
要删除的为X上一个元素为Y,下一个元素为Z。由于X下面有子孩子Z所以想删除X必须让Y元素跨过X直接连接到Z,然后把中间的元素X删掉。
左右都有树的话,找到要删除节点右子树的最小的节点,因为他不可能有左孩子,所他跟要删除的对象互换位置然后用删除单个孩子的方法删除。
AVL树
如图4-28,这是一颗不好的二叉树,他的查找效率是直线型的O(n),就是最坏得树形结构,所以我们推荐使用平衡二叉树(AVL)。
以下内容转载自:http://blog.csdn.net/gabriel1026/article/details/6311339
感谢这位朋友 讲的确实很容易理解。
平衡二叉树在进行插入操作的时候可能出现不平衡的情况,AVL树即是一种自平衡的二叉树,它通过旋转不平衡的节点来使二叉树重新保持平衡,并且查找、插入和删除操作在平均和最坏情况下时间复杂度都是O(log n)
AVL树的旋转一共有四种情形,注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。
1. LL型
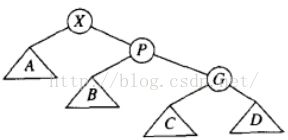
平衡二叉树某一节点的左孩子的左子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向右旋转一次即可,如图所示,原A的左孩子B变为父结点,A变为其右孩子,而原B的右子树变为A的左子树,注意旋转之后Brh是A的左子树(图上忘在A于Brh之间标实线)
2. RR型
平衡二叉树某一节点的右孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向左旋转一次即可,如图所示,原A右孩子B变为父结点,A变为其左孩子,而原B的左子树Blh将变为A的右子树。
3. LR型
平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,这时还需要再向右旋转一次。
4. RL型
平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。
经过上面的讲述我相信很多人都能理解单双旋转了。
最后一个是哈弗曼树,也就是最优二叉树,效率最高。下图就是一个完美树
构造哈弗曼树
引自:http://blog.csdn.net/shuangde800/article/details/7341289
三、哈夫曼树的在编码中的应用
- #include
- #include
- #include
- using namespace std;
- #define N 10 // 带编码字符的个数,即树中叶结点的最大个数
- #define M (2*N-1) // 树中总的结点数目
- class HTNode{ // 树中结点的结构
- public:
- unsigned int weight;
- unsigned int parent,lchild,rchild;
- };
- class HTCode{
- public:
- char data; // 待编码的字符
- int weight; // 字符的权值
- char code[N]; // 字符的编码
- };
- void Init(HTCode hc[], int *n){
- // 初始化,读入待编码字符的个数n,从键盘输入n个字符和n个权值
- int i;
- printf("input n = ");
- scanf("%d",&(*n));
- printf("\ninput %d character\n",*n);
- fflush(stdin);
- for(i=1; i<=*n; ++i)
- scanf("%c",&hc[i].data);
- printf("\ninput %d weight\n",*n);
- for(i=1; i<=*n; ++i)
- scanf("%d",&(hc[i].weight) );
- fflush(stdin);
- }//
- void Select(HTNode ht[], int k, int *s1, int *s2){
- // ht[1...k]中选择parent为0,并且weight最小的两个结点,其序号由指针变量s1,s2指示
- int i;
- for(i=1; i<=k && ht[i].parent != 0; ++i){
- ; ;
- }
- *s1 = i;
- for(i=1; i<=k; ++i){
- if(ht[i].parent==0 && ht[i].weight
- *s1 = i;
- }
- for(i=1; i<=k; ++i){
- if(ht[i].parent==0 && i!=*s1)
- break;
- }
- *s2 = i;
- for(i=1; i<=k; ++i){
- if(ht[i].parent==0 && i!=*s1 && ht[i].weight
- *s2 = i;
- }
- }
- void HuffmanCoding(HTNode ht[],HTCode hc[],int n){
- // 构造Huffman树ht,并求出n个字符的编码
- char cd[N];
- int i,j,m,c,f,s1,s2,start;
- m = 2*n-1;
- for(i=1; i<=m; ++i){
- if(i <= n)
- ht[i].weight = hc[i].weight;
- else
- ht[i].parent = 0;
- ht[i].parent = ht[i].lchild = ht[i].rchild = 0;
- }
- for(i=n+1; i<=m; ++i){
- Select(ht, i-1, &s1, &s2);
- ht[s1].parent = i;
- ht[s2].parent = i;
- ht[i].lchild = s1;
- ht[i].rchild = s2;
- ht[i].weight = ht[s1].weight+ht[s2].weight;
- }
- cd[n-1] = '\0';
- for(i=1; i<=n; ++i){
- start = n-1;
- for(c=i,f=ht[i].parent; f; c=f,f=ht[f].parent){
- if(ht[f].lchild == c)
- cd[--start] = '0';
- else
- cd[--start] = '1';
- }
- strcpy(hc[i].code, &cd[start]);
- }
- }
- int main()
- {
- int i,m,n,w[N+1];
- HTNode ht[M+1];
- HTCode hc[N+1];
- Init(hc, &n); // 初始化
- HuffmanCoding(ht,hc,n); // 构造Huffman树,并形成字符的编码
- for(i=1; i<=n; ++i)
- printf("\n%c---%s",hc[i].data,hc[i].code);
- printf("\n");
- return 0;
- }