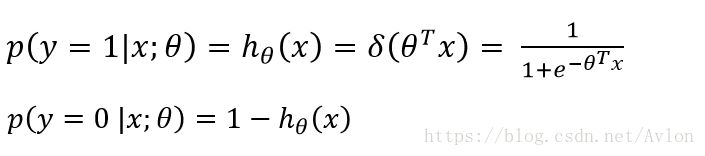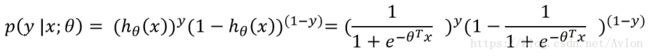机器学习作业-Logistic Regression（逻辑回归）

ML课堂的第二个作业，逻辑回归要求如下：

数据集链接如下：

http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex4/ex4.html

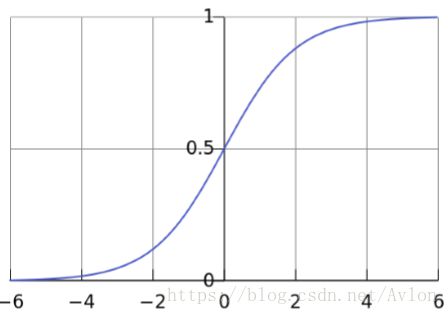
逻辑回归的关键是运用了sigmod函数，sigmod函数有一个很好的性质是其导函数很好求

函数图像：

sigmod会将函数值映射到（0，1）区间内，将其输出值看作是概率则有逻辑回归的二分类模型：

上式很好理解，sigmod(x)是x属于pos类的概率则x属于neg类的概率自然就是1-sigmod(x)，两式子组合一下可得到下式：

上式其实就是一个概率密度函数，对θ做最大似然估计，使最大似然函数求到最大值。

用梯度下降法，梯度和更新公式如下：

题目要求用GD、SGD还有牛顿法目前实现了GD和SGD的，牛顿法会在后面更新，需要提到的是数据需要进行归一化，不然由于计算机内浮点数精度原因sigmod函数会取到1，log(sigmod）会出log(0）错，后面用tensorflow实现的版本用adam优化在不进行归一化的情况下可以收敛。

首先是梯度下降的代码

nolinear.py里面封装了一下sigmod函数

import math
def sigmods(x):
    return 1/(math.exp(-x)+1)

 

然后是主文件：

import nolinear as nl
import numpy as np
import matplotlib.pyplot as plt
import math

data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")

plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
    if data_y[i] == 1:
        plt.plot(data_x[i][0], data_x[i][1], 'b+')
    else:
        plt.plot(data_x[i][0], data_x[i][1], 'bo')

mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance

data_y = data_y.reshape(-1, 1)          # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[data_x, temp]

learn_rate = 0.1
theda = np.zeros([3])

loss = 0
old_loss = 0

for i in range(data_y.size):
    if data_y[i] == 1:
        loss += math.log10(nl.sigmods(np.matmul(data_x[i], theda)))
    else:
        loss += math.log10(1-nl.sigmods(np.matmul(data_x[i], theda)))

while abs(loss-old_loss) > 0.001:
    temp = np.matmul(data_x, theda)
    dew = np.zeros([3])
    for i in range(data_y.size):
        dew += (data_y[i]-nl.sigmods(temp[i]))*data_x[i]
    theda = theda+learn_rate*dew
    old_loss = loss
    loss = 0
    for i in range(data_y.size):
        if data_y[i] == 1:
            loss += math.log10(nl.sigmods(np.matmul(data_x[i], theda)))
        else:
            loss += math.log10(1 - nl.sigmods(np.matmul(data_x[i], theda)))
    print(-old_loss)
plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
    plot_y[i-16] = -(theda[2]+theda[0]*((i-mean[0])/variance[0]))/theda[1]
    plot_y[i - 16] = plot_y[i-16]*variance[1]+mean[1]
plt.plot(plot_x, plot_y)
plt.show()

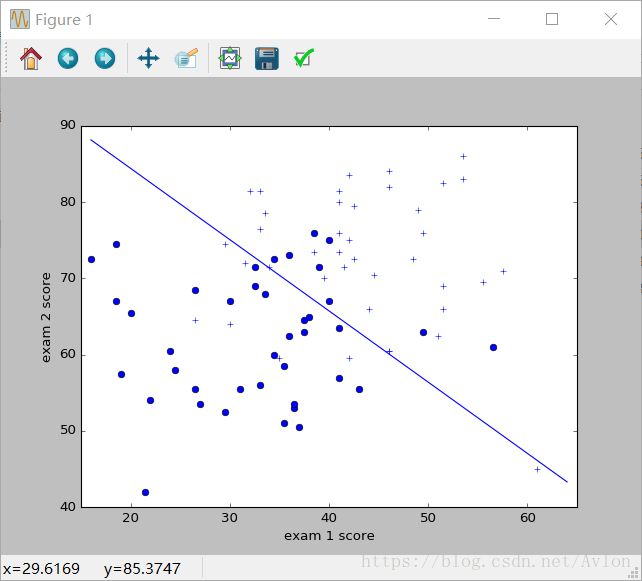
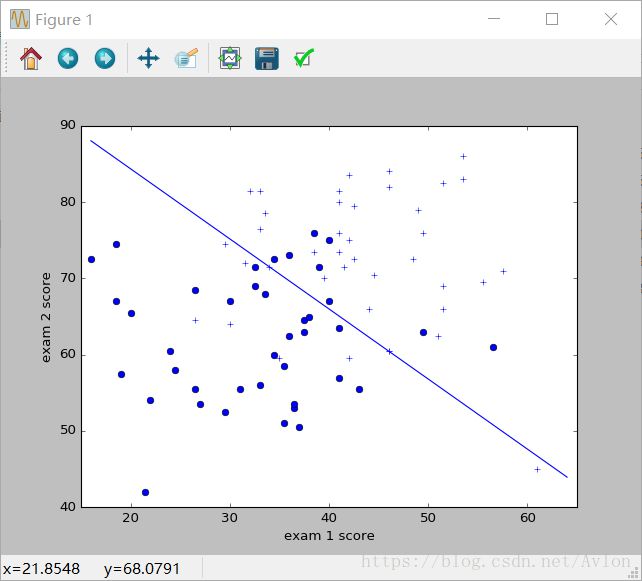
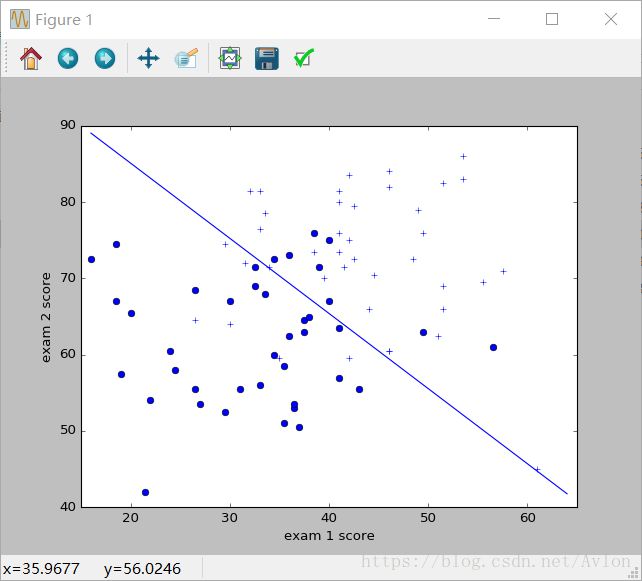
最后得到结果：

loss函数的值可以看到几步就收敛了，跟同学比有点过快，现在还没搞明白原因

接着给出SGD的代码，SGD每次随机抽取两个样本进行梯度下降

import nolinear as nl
import numpy as np
import matplotlib.pyplot as plt
import math
import random

data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")

plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
    if data_y[i] == 1:
        plt.plot(data_x[i][0], data_x[i][1], 'b+')
    else:
        plt.plot(data_x[i][0], data_x[i][1], 'bo')

mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance

data_y = data_y.reshape(-1, 1)          # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[data_x, temp]

learn_rate = 0.1
theda = np.zeros([3])

loss = 0
old_loss = 0

for i in range(data_y.size):
    if data_y[i] == 1:
        loss += math.log10(nl.sigmods(np.matmul(data_x[i], theda)))
    else:
        loss += math.log10(1-nl.sigmods(np.matmul(data_x[i], theda)))

while abs(loss-old_loss) > 0.001:
    temp = np.matmul(data_x, theda)
    dew = np.zeros([3])
    j = random.randint(0, data_y.size-1)
    dew += (data_y[j]-nl.sigmods(temp[j]))*data_x[j]
    z = random.randint(0, data_y.size - 1)
    while j == z:
        z = random.randint(0, data_y.size - 1)
    dew += (data_y[z] - nl.sigmods(temp[z])) * data_x[z]
    theda = theda+learn_rate*dew
    old_loss = loss
    loss = 0
    for i in range(data_y.size):
        if data_y[i] == 1:
            loss += math.log10(nl.sigmods(np.matmul(data_x[i], theda)))
        else:
            loss += math.log10(1 - nl.sigmods(np.matmul(data_x[i], theda)))
    print(-old_loss)
plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
    plot_y[i-16] = -(theda[2]+theda[0]*((i-mean[0])/variance[0]))/theda[1]
    plot_y[i - 16] = plot_y[i-16]*variance[1]+mean[1]
plt.plot(plot_x, plot_y)
plt.show()

 

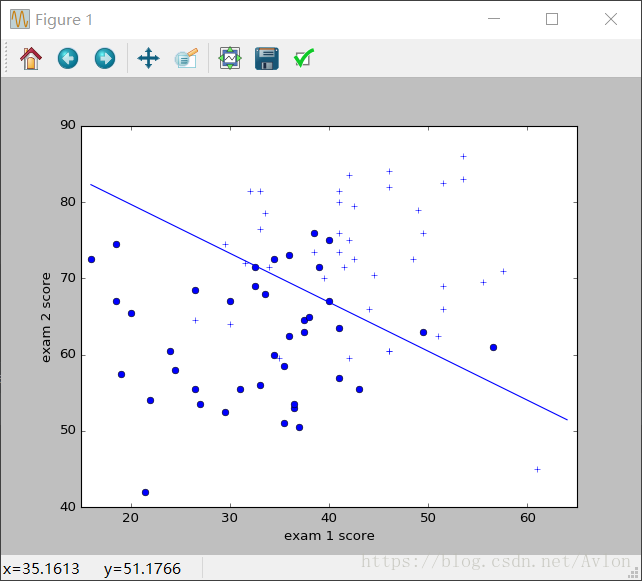
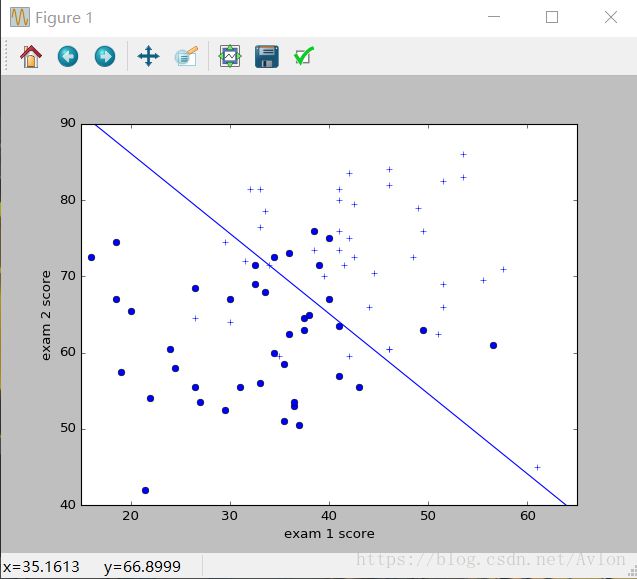
每次运行sgd其结果都不一定一样，但是loss值都是收敛于14左右，运行结果图示：

第二次运行

loss的变化：

tensorflow实现版

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")


plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
    if data_y[i] == 1:
        plt.plot(data_x[i][0], data_x[i][1], 'b+')
    else:
        plt.plot(data_x[i][0], data_x[i][1], 'bo')
data_y = data_y.reshape(-1, 1)
x = tf.placeholder("float", [None, 2])
y = tf.placeholder("float", [None, 1])

w = tf.Variable(tf.zeros([2, 1]))
bias = tf.Variable(tf.zeros([1, 1]))
z = tf.matmul(x, w)+bias
xita = w
b = bias
loss = tf.reduce_sum(y*tf.log(tf.sigmoid(z))+(1-y)*tf.log(1-tf.sigmoid(z)))
tf.summary.scalar("loss_function", -loss)

train_opt = tf.train.AdamOptimizer(0.1).minimize(-loss)

merge = tf.summary.merge_all()

init = tf.global_variables_initializer()
summary_writer = tf.summary.FileWriter("log", tf.get_default_graph())

sess = tf.Session()
sess.run(init)

for i in range(1000):
    train, loss_value, w_value, b_value, summary = sess.run([train_opt, loss, xita, b, merge], feed_dict={x: data_x, y: data_y})
    summary_writer.add_summary(summary, i)
    print(loss_value)
w_value = np.array(w_value)
w_value = w_value.reshape(-1)
b_value = np.array(b_value)
plot_y = np.zeros(65 - 16)
plot_x = np.arange(16, 65)
for j in range(16, 65):
    plot_y[j - 16] = -(b_value[0] + w_value[0] * j) / w_value[1]
plt.plot(plot_x, plot_y)
plt.show()


summary_writer.close()

结果图：

更新一下牛顿法、

牛顿法其实就是求二阶导数，用一个二次函数去做当前点的拟合，其收敛速度非常快，不过因为复杂的运算所以实际应用很少，我这里遇到几个坑主要是numpy中 array和met之间的差别，下面给出代码和结果

import numpy as np
import matplotlib.pyplot as plt


data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")

plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
    if data_y[i] == 1:
        plt.plot(data_x[i][0], data_x[i][1], 'b+')
    else:
        plt.plot(data_x[i][0], data_x[i][1], 'bo')

mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance

data_y = data_y.reshape(-1, 1)          # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[temp, data_x]
data_x = np.mat(data_x)

learn_rate = 0.1
theda = np.mat(np.zeros([3, 1]))

loss = 0
old_loss = 0


def get_loss(h):
    l1 = data_y.T*np.log(h)
    l2 = (1-data_y).T*np.log((1-h))
    return np.multiply(1/data_y.size, sum(-l1-l2))


loss = get_loss(1.0/(1+np.exp(-(data_x*theda))))

while abs(old_loss-loss) > 0.000001:
    h = 1.0/(1+np.exp(-(data_x*theda)))
    J = np.multiply(1.0/data_y.size, data_x.T*(h-data_y))
    H = np.multiply(1.0/data_y.size, data_x.T*np.diag(np.multiply(h, (1-h)).T.getA()[0])*data_x)
    theda = theda-H.I*J
    old_loss = loss
    loss = 0
    loss = get_loss(h)

plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
    plot_y[i - 16] = -(theda[0] + theda[2] * ((i - mean[0]) / variance[0])) / theda[1]
    plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
plt.plot(plot_x, plot_y)
plt.show()

基本上一步收敛

结果：

打印损失函数值的变化发现只迭代了一次