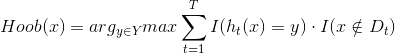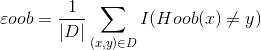集成学习-Bagging原理与实现 西瓜书

Bagging简介

Bagging是并行式集成学习的最著名代表，名字是由Bootstrap AGGregatING缩写而来，看到Bootstrap我们就会联想到boostrap的随机模拟法和它对应的样本获取方式，它是基于自助采样法（Boostrap sampleing），Bagging也是同理.给定包含m个样本的数据集，先随机抽取一个样本放入采样集中，再把该样本放回，使得下次采样时该样本仍有机会被选中，这样经过m次采样，我们便从原始是数据集中抽取样本得到一个数据量同为m的数据集.说简单一点就是统计里的有放回抽样，且每个样本被抽取的概率相同，均为总样本数分之一.

1）样本抽取方式

假设一个样本被抽取的概率是1/m，有：

                                                                        

意味着抽样次数足够大时，一个样本不被抽到的概率为36.8%,由此可知，初始样本约有63.2%的样本出现在采样集中.这样我们可以采样T次，从而得到T个含m个训练样本的采样集，基于每个训练集样本训练一个学习器，最后结合这些学习器的结果，预测总结果,这就是Bagging的大致实现过程，针对最后的预测，Bagging一般采取投票法，若票数相同，则最简单的方法是是随机选择一个，当然也可以进一步考察学习器的投票置信度，或者使用加权投票法等处理最终结果.

2）时间复杂度

这里基学习器可以选择DT，LR，NB，SVM，神经网络等等，假定基学习期的时间复杂度为O(m),则bagging的复杂度大约为T(O(m)+O(s)),考虑到采样与投票的平均过程复杂度O(s)很小，而T通常是一个不太大的常数，所以Bagging的集成与直接使用基学习器算法训练一个学习器的时间复杂度同阶，这说明Bagging是一个很高效的集成学习算法，另外，与AdaBoost只适用于二分类任务不同，Bagging可以用于多分类，回归的任务.

3）优缺点

Bagging的个优点是对泛化性能的估计，这得益于自助采样法，由于训练只使用了63.2%的样本，因此剩下约36.8%的样本可当做测试集来对泛化性能进行‘包外估计’，为此需记录每个基学习器所使用的训练样本，不放令Dt表示学习器ht实际使用的训练样本集，令H_oob(x)表示对有样本x的包外预测，即测试集不包含数据集中用于训练的部分：

                                                    

则Bagging的泛化误差的包外估计为：

                                                    

利用包外估计的优点，我们可以在基学习器的训练过程中及时调整训练模型，例如在使用决策树为基学习器时，可以根据泛化性能来辅助剪枝，而当使用神经网络时，则可利用包外样本来辅助早停从而减少过拟合的风险.

自助采样法优点比较明显，但在数学上也有一定的缺陷，重复有放回采样的道德样本集改变了数据原有的分布，因此在一定程度上引入了偏差，对最终的结果预测会造成一定程度的影响.

Bagging实现

            

这是西瓜书上给出的Bagging伪代码，我们需要做的很简单，确定基学习算法，训练轮数T，利用自助法提取训练集，最后选择使误差最小的y作为预测样本的标签.

导入所需库

from numpy import *
import matplotlib.pyplot as plt
import random
from sklearn import tree

这里常用的num库和mattplot库就不多赘述了，random库负责随机选取样本实现自助采样法，sklearn.tree负责使用决策树作为基学习器.

读取数据

def loadDataSet(fileName):#读取数据
    numFeat = len(open(fileName).readline().split('\t')) 
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat-1):#添加数据
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))#添加数据对应标签
    return dataMat,labelMat

这里的数据来源《机器学习实战》第七章的病马数据，数据包含多匹患有疝气病的1马的多项特征指标，而标签值对应病马的死亡率预测，+1对应存活，-1对应死亡，通过决策树和Bagging，来预测病马的生存情况.

自助法采样

def rand_train(dataMat,labelMat):#自助法采样
    len_train = len(labelMat)#获取样本1数
    train_data = [] ; train_label = []
    for i in range(len_train):#抽取样本数次样本
        index = random.randint(0,len_train-1)#随机生成样本索引
        train_data.append(dataMat[index])#添加对应数据与标签
        train_label.append(labelMat[index])
    return train_data,train_label#返回训练集与训练集标签

通过random.randint随机生成样本数范围内的索引，构造Bagging数据集.

决策树基学习器

def bagging_by_tree(dataMat,labelMat,t=10):#默认并行生成十个基学习器
    test_data,test_label = loadDataSet('horseColicTest2.txt')  #获取测试样本与标签   
    predict_list = []
    for i in range(t):#并行生成T个
        train_data,train_label = rand_train(dataMat,labelMat)#自主采样1得到样本
        clf = tree.DecisionTreeClassifier()#初始化决策树模型
        clf.fit(train_data,train_label)#训练模型
        total = []
        y_predicted = clf.predict(test_data)#预测数据
        total.append(y_predicted)
        predict_list.append(total)#结果添加到预测列表中
    return predict_list,test_label

默认t=10，即产生十个基学习器，这里基学习器对应决策树Tree，通过t次采样，获得t个样本，训练t个决策树，将每次预测的结果添加到predict_list中，供之后计算准确率.

汇总结果计算准确率

def calc_error(predict_list,test_label):#计算错误率
    m,n,k = shape(predict_list)#提取预测集信息
    predict_label = sum(predict_list,axis = 0)
    predict_label = sign(predict_label)
    for i in range(len(predict_label[0])):
        if predict_label[0][i] == 0:#如果票数相同，则随机生成一个标签
            tip = random.randint(0,1)
            if tip == 0:
                predict_label[0][i] = 1
            else:
                predict_label[0][i] =-1
    error_count = 0#初始化预测错误数
    for i in range(k):
        if predict_label[0][i] != test_label[i]:#判断预测精度
            error_count += 1
    error_rate = error_count/k
    return error_rate

针对十个基学习器的预测结果，将结果累加，并使用sign函数进行类别预测，对于投票数相同的样例，按照最简单的解决方式，随机选择一个类别添加，最终统计预测不对的类别，最终计算错误率.

主函数

if __name__ == "__main__":
    fileName = 'horseColicTraining2.txt'
    dataMat,labelMat =  loadDataSet(fileName)
    train_data,train_label = rand_train(dataMat,labelMat)
    predict_list , test_label = bagging_by_tree(dataMat,labelMat)
    print("Bagging错误率：",calc_error(predict_list,test_label))

运行结果

Bagging错误率： 0.26865671641791045
[Finished in 0.9s]

改为单学习器

def bagging_by_Onetree(dataMat,labelMat,t=10):
    test_data,test_label = loadDataSet('horseColicTest2.txt') 
    train_data,train_label = rand_train(dataMat,labelMat)
    clf = tree.DecisionTreeClassifier()
    clf.fit(train_data,train_label)
    y_predicted = clf.predict(test_data)
    error_count = 0
    for i in range(67):
        if y_predicted[i] != test_label[i]:
            error_count += 1
    return error_count/67

将bagging_by_tree函数稍微修改，取消学习器个数t，得到单一学习器，训练样本，计算错误率看看如何.

Bagging错误率： 0.22388059701492538
单一学习器错误率: 0.3582089552238806
[Finished in 0.9s]

总结

将上述过程多次计算，每次结果都会有所不同，这是因为随机抽样造成的样本扰动所致，而且针对此样本集，虽然集成后会提升性能，但Bagging最后的泛性能并不是很理想，因此还有更好的分类模型去预测，这里只是大概实现Bagging的过程，从而加深集成学习的印象.接下来主要介绍随机森林RF，随机森林在Bagging样本扰动的基础上，还对属性进行了随机选取，大大提升了模型泛化能力，是当前集成学习特别常见的模型.