朴素贝叶斯 (Naive Bayes)

朴素贝叶斯 (Naive Bayes)

前言

贝叶斯定理概率论中必学的一个定理，而朴素贝叶斯就是基于此的一种简单分类方法。

朴素贝叶斯（naive Bayes）法是是基于 贝叶斯定理 和 特征条件独立假设 的分类方法

数学解释

条件独立公式，如果X和Y相互独立，则有：

$$P(X,Y)=P(X)P(Y)$$

条件概率公式：

$$P(Y|X)=\frac{P(X,Y)}{P(X)}$$

$$P(X|Y)=\frac{P(X,Y)}{P(Y)}$$

先验概率P(A)：在不考虑任何情况下，A事件发生的概率。

条件概率P(B|A)：A事件发生的情况下，B事件发生的概率。

后验概率P(A|B)：在B事件发生之后，对A事件发生的概率的重新评估。

全概率：如果A和A’构成样本空间的一个划分，那么事件B的概率为：A和A’的概率分别乘以B对这两个事件的概率之和。

$$P(B)=\sum _{i=1}^{n}P(A_i)\ast P(B|A)$$

将后验概率和全概率公式进行组合就可以得到贝叶斯公式

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{P(B|A)P(A)}{\sum _{i=1}^{n}P(A_i)\ast P(B|A)}$$

分类问题：

定义： 已知集合 $I=\{x_1,x_2,...,x_m,...\}$ 和 $C=\{y_1,y_2,...,y_m,...\}$ ,，确定映射规则 $y=f(x)$ ,使得任意 $x_i\in I$ 有且仅有一个 $y_i\in C$ ,使得 $y_i=f(x_i)$ 成立。

其中C叫做类别集合，其中每一个元素是一个类别，而I叫做项集合（特征集合），其中每一个元素是一个待分类项，f叫做分类器。分类算法的任务就是构造分类器f。

所以贝叶斯公式换个格式如下：

$$P(类别|特征)=\frac{P(特征|类别)P(类别)}{P(特征)}$$

朴素贝叶斯分类:

朴素贝叶斯(Naive Bayes，NB)是基于特征之间是独立的这一朴素假设，应用贝叶斯定理的监督学习算法对应给定的样本 $X$ 的特征向量$x_1,x_2,...,x_m$；该样本 $X$ 的类别 $y$ 的概率可以由贝叶斯公式得到：

$$P(y|x_1,x_2,...,x_m)=\frac{P(x_1,x_2,...,x_m|y)P(y)}{P(x_1,x_2,...,x_m)}$$

由于特征之间是独立的，所以

$$P(y|x_1,x_2,...,x_m)=\frac{P(x_1,x_2,...,x_m|y)P(y)}{P(x_1,x_2,...,x_m)}=\frac{{\prod }_{i=1}^{n}P(x_i|y)P(y)}{P(x_1,x_2,...,x_m)}$$

在给定样本的情况下，$P(x_1,x_2,...,x_m)$ 是常数，所以得到

$$P(y|x_1,x_2,...,x_m)\propto \prod _{i=1}^{n}P(x_i|y)P(y)$$

模型化简为

$$\hat{y}=argmax(y)\prod _{i=1}^{n}P(x_i|y)$$

后验概率最大等价于0-1损失函数时的期望风险最小化

极大似然估计：

先验概率

$$\hat{P}(y)=\frac{\sum _{i=1}^{n}I(y_i)}{N}$$

$N$ 为训练集中样本点数, $I$ 是指示函数，满足括号内条件时为1否则为0；可以看作为计数

条件概率

设第 $j$ 维特征的取值空间为 $\{a_{j1},a_{j2},\cdots ,a_{jSj}\}$，且输入变量的第 $j$ 维 $x^{(j)}=a_{jl}$，则条件概率的极大似然估计：

$$\hat{P}(x^{(j)}=a_{jl}|y)=\frac{\sum _{i=1}^{n}I(x^{(j)}=a_{jl},y)}{I(y)}$$

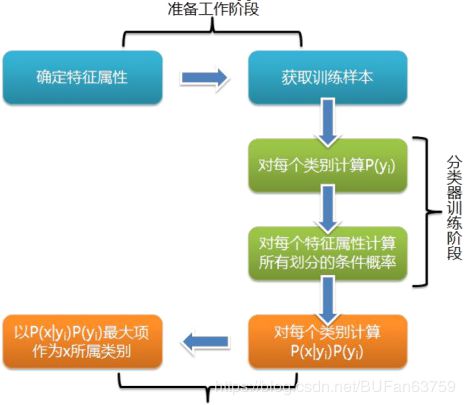
算法思想

通过考虑特征概率来预测分类

如果一个事物在一些属性条件发生的情况下，事物属于A的概率>属于B的概率，则判定事物属于A

算法步骤

1、分解各类先验样本数据中的特征

2、计算各类数据中，各特征的条件概率

（比如：特征1出现的情况下，属于A类的概率p(A|特征1)，属于B类的概率p(B|特征1)，属于C类的概率p(C|特征1)…）

3、分解待分类数据中的特征（特征1、特征2、特征3、特征4…）

4、计算各特征的各条件概率的乘积，如下所示：

判断为A类的概率：p(A|特征1)*p(A|特征2)*p(A|特征3)*p(A|特征4)…

判断为B类的概率：p(B|特征1)*p(B|特征2)*p(B|特征3)*p(B|特征4)…

判断为C类的概率：p(C|特征1)*p(C|特征2)*p(C|特征3)*p(C|特征4)…

…

5、结果中的最大值就是该样本所属的类别

朴素贝叶斯算法特点

优点: 在数据较少的情况下仍然有效，可以处理多类别问题。
缺点: 对于输入数据的准备方式较为敏感。
适用数据类型: 标称型数据。

Python实现

构建一个快速过滤器来屏蔽在线社区留言板上的侮辱性言论。如果某条留言使用了负面或者侮辱性的语言，那么就将该留言标识为内容不当。对此问题建立两个类别: 侮辱类和非侮辱类，使用 1 和 0 分别表示。

收集数据: 可以使用任何方法

准备数据: 从文本中构建词向量

分析数据: 检查词条确保解析的正确性

训练算法: 从词向量计算概率

测试算法: 根据现实情况修改分类器

使用算法: 对社区留言板言论进行分类

收集数据: 可以使用任何方法

以下代码参照《机器学习实战》第四章

#!/usr/bin/python
# coding=utf-8
from numpy import *
# 过滤网站的恶意留言 侮辱性：1 非侮辱性：0
# 创建一个实验样本
def loadDataSet():
  postingList = [['my','dog','has','flea','problems','help','please'],
          ['maybe','not','take','him','to','dog','park','stupid'],
          ['my','dalmation','is','so','cute','I','love','him'],
          ['stop','posting','stupid','worthless','garbage'],
          ['mr','licks','ate','my','steak','how','to','stop','him'],
          ['quit','buying','worthless','dog','food','stupid']]
  classVec = [0,1,0,1,0,1]
  return postingList, classVec
# 创建一个包含在所有文档中出现的不重复词的列表
def createVocabList(dataSet):
  vocabSet = set([])   # 创建一个空集
  for document in dataSet:
    vocabSet = vocabSet | set(document)  # 创建两个集合的并集
  return list(vocabSet)
# 将文档词条转换成词向量
def setOfWords2Vec(vocabList, inputSet):
  returnVec = [0]*len(vocabList)    # 创建一个其中所含元素都为0的向量
  for word in inputSet:
    if word in vocabList:
      # returnVec[vocabList.index(word)] = 1 # index函数在字符串里找到字符第一次出现的位置 词集模型
      returnVec[vocabList.index(word)] += 1   # 文档的词袋模型 每个单词可以出现多次
    else: print "the word: %s is not in my Vocabulary!" % word
  return returnVec
# 朴素贝叶斯分类器训练函数 从词向量计算概率
def trainNB0(trainMatrix, trainCategory):
  numTrainDocs = len(trainMatrix)
  numWords = len(trainMatrix[0])
  pAbusive = sum(trainCategory)/float(numTrainDocs)
  # p0Num = zeros(numWords); p1Num = zeros(numWords)
  # p0Denom = 0.0; p1Denom = 0.0
  p0Num = ones(numWords);  # 避免一个概率值为0,最后的乘积也为0
  p1Num = ones(numWords);  # 用来统计两类数据中，各词的词频
  p0Denom = 2.0; # 用于统计0类中的总数
  p1Denom = 2.0 # 用于统计1类中的总数
  for i in range(numTrainDocs):
    if trainCategory[i] == 1:
      p1Num += trainMatrix[i]
      p1Denom += sum(trainMatrix[i])
    else:
      p0Num += trainMatrix[i]
      p0Denom += sum(trainMatrix[i])
      # p1Vect = p1Num / p1Denom
      # p0Vect = p0Num / p0Denom
  p1Vect = log(p1Num / p1Denom)  # 在类1中，每个次的发生概率
  p0Vect = log(p0Num / p0Denom)   # 避免下溢出或者浮点数舍入导致的错误 下溢出是由太多很小的数相乘得到的
  return p0Vect, p1Vect, pAbusive
# 朴素贝叶斯分类器
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
  p1 = sum(vec2Classify*p1Vec) + log(pClass1)
  p0 = sum(vec2Classify*p0Vec) + log(1.0-pClass1)
  if p1 > p0:
    return 1
  else:
    return 0
def testingNB():
  listOPosts, listClasses = loadDataSet()
  myVocabList = createVocabList(listOPosts)
  trainMat = []
  for postinDoc in listOPosts:
    trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
  p0V, p1V, pAb = trainNB0(array(trainMat), array(listClasses))
  testEntry = ['love','my','dalmation']
  thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
  print testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb)
  testEntry = ['stupid','garbage']
  thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
  print testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb)
# 调用测试方法----------------------------------------------------------------------
testingNB()