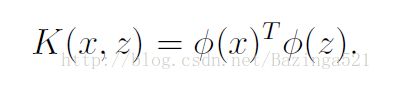斯坦福机器学习2:SVM支持向量机的通俗理解
暑假一直在学吴恩达老师的机器学习公开课,学习前面还都比较好理解,根据公式基本上可以实现用matlab编程编出来,然而从第七节课开始讲的SVM算法开始听的迷迷糊糊,在听了两三遍开头,然后又买了几本工具书翻了翻,终于搞懂了一点点,所以写写笔记,笔记中用到了周志华老师对最优间隔分隔器的理解,其余的内容都是用了视频里的知识。还有在知乎里找的比较好理解的资料,笔记内容没有太多数学推导,比较肤浅,但是在我看来比较容易理解。
1首先支持向量机的符号
类别不再是{0,1},而变成了{-1,1},这样对函数间隔的表示会更方便
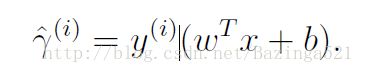
这样正样本当wTx+b尽量大的正数时结果越可靠
负样本当wTx+b尽量小时结果越可靠
θTx也变成了wT+b,这样b取代了x中一列1的作用
2最优间隔分类器
在最优间隔分类器中他讲了很多不同的表示方法,看起来很复杂,在周志华的机器学习书中表示的很简单,原理也讲得过去,几种表示方法的表示方式结果相同

距离不为负数,所以上面的分子加绝对值
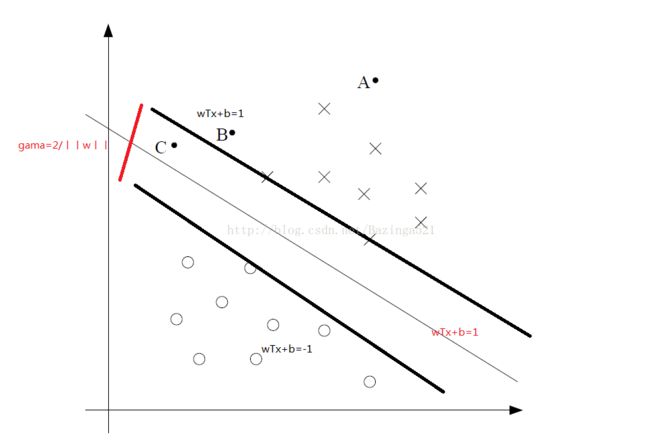
这样所要求的问题就是
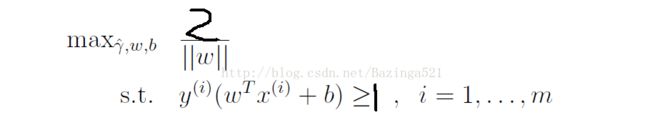
等价于
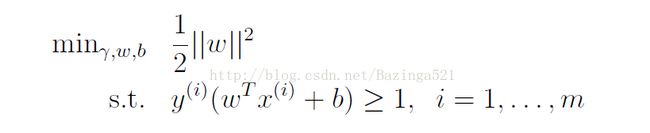
上面这个式子就和斯坦福视频里面讲的#3标书一致了,然后就是求对偶问题的讲解,具体过程自己看一下,这里是抛开了SVM算法在讲数学的知识。
将上面讲的求对偶问题的想法应用到SVM算法中,可以求到上述公式的对偶问题为
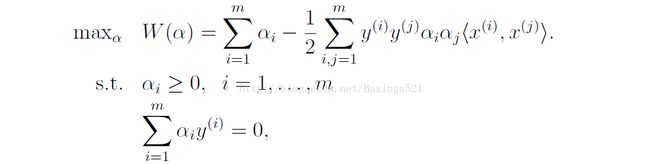
这样根据后面要讲的SMO算法求解出α,然后由求解对偶问题中间的过程中公式

求解出w,根据公式
求解出b。
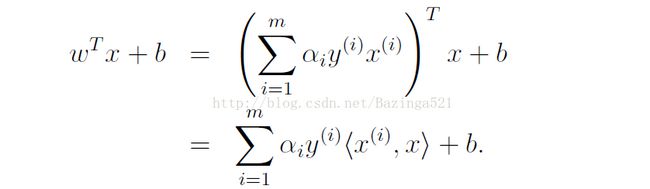
这样对于分类问题,w不需要显式的表示,直接用内积求wT+b就可以了 (这句话理解不了没关系,往下看完再看这句话就理解了)
就可以求出他的类别是1还是-1了
注意看
在这里引出了核技法,在知乎上看了一个很有趣的帖子讲核技法。
对于原始的SVM,就是某一个大侠找一根棍子分开两种球
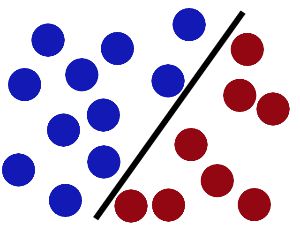
但是如果数据是这样的呢?
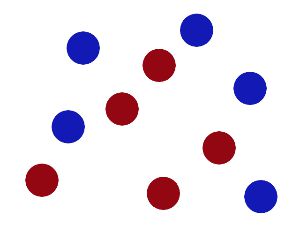
可以看到在二维空间内很难区分开来两种球。大侠没有棍可以很好帮他分开两种球了,现在怎么办呢?当然像所有武侠片中一样大侠桌子一拍,球飞到空中。然后,凭借大侠的轻功,大侠抓起一张纸,插到了两种球的中间。
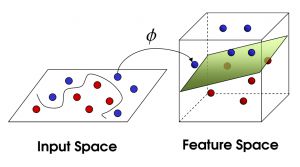
从二维空间看好像是一根曲线把他们分开了,这就是核技法,把数据映射到三维空间或者更高维空间用一个平面或者超平面把数据分开。
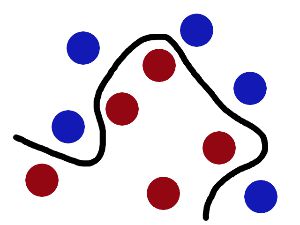
而刚刚的式子中向量不用显式的表示刚好对核技法提供了莫大的支持。
我们定义核函数X,Z就是上面的x(j)和x(i)为了简化,去掉上标。
Φ(x)和Φ(z)就是高维空间中的向量了,而这里并不用显式的表示,因为上述的求解问题就变成了

举一个例子。
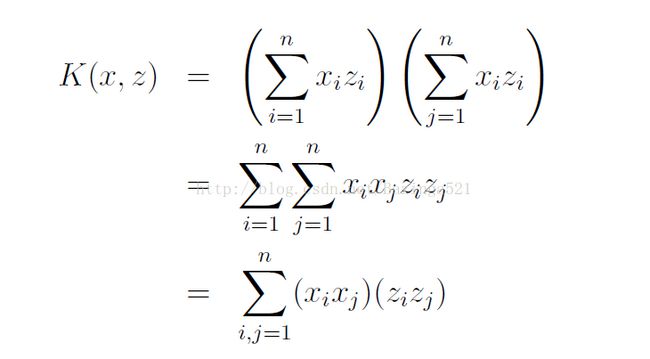
对应的映射函数为
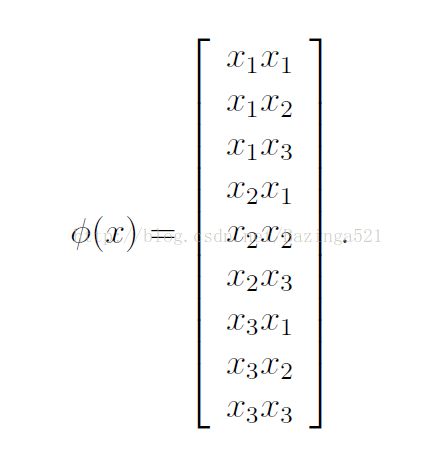
在引入了核函数之后只需要将两个特征向量的值带进去求得核函数就可以了,并不用表示出复杂的高维向量Φ(x),这样就好像上面说的大侠把求击到了空中。
视频中还讲了其他的核函数,线性核函数,高斯核函数等等。
最后一节讲了SMO算法求解上面那个很复杂的凸函数,求解出来最优的α,然后再求w,求b,问题迎刃而解。