机器学习—逻辑回归Logistic Regression
8.逻辑回归
8.1逻辑回归的实现
8.1.1什么是逻辑回归
逻辑回归又称Logistic Regression，其本质是一种广义的线性回归模型，常用于解决二分类问题。
在前面的多元线性回归中，有
，其中
表示样本的预测值、Xb表示样本的特征集加上第一列的元素1、θ表示截距和特征的系数。
在逻辑回归中，有函数
，当
>=0.5时，
=1；当
<=0.5时，
=0。这也是为什么逻辑回归用于解决二分类问题的原因，其
中表示样本发生的概率。
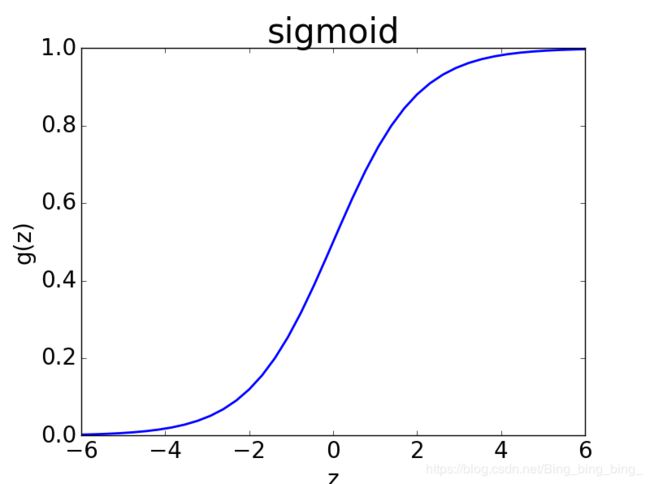
多元线性回归中，
的阈值处于(-∞,+∞)，为了将其映射到(0,1)之间，需要一个更好的映射函数，这就是sigmoid函数：
函数曲线如下所示：
因此，逻辑回归算法：
由于在numpy中，向量乘矩阵和矩阵乘向量的结果相同，因此，也有人写成
并带入sigmoid函数。
当真实值y=1时，若
越小，对应的损失值也越大，因此损失函数J是
的递减函数，可以表示为J=-log()、∈(0,1)、y=1。
当真实值y=0，若越大，对应的损失值也越大，因此损失函数J是的递增函数，可以表示为J=-log(1-)、∈(0,1)、y=1。
综上，对于每个样本有损失函数J(i)=-y(i)log((i))-(1-y(i))log(1-(i))；对于所有样本有损失函数：
使用梯度下降法求损失函数的极小值，这里不再列推导过程，损失函数的梯度如下所示：
8.1.2自己实现逻辑回归算法
#程序8-1
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
#取出鸢尾花前2个种类
X = X[y<2]
y = y[y<2]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
def sigmoid(t):
return 1./(1.+np.exp(-t))
def logic_J(X_b,y,theta):
p_hat = sigmoid(X_b.dot(theta))
return -np.sum(y*np.log(p_hat)+(1-y)*np.log(1-p_hat))/len(y)
def logic_dJ(X_b,y,theta):
p_hat = sigmoid(X_b.dot(theta))
return X_b.T.dot(p_hat-y)/len(y)
def logic_pedict(X_b,theta):
p_hat = sigmoid(X_b.dot(theta))
return np.array(p_hat>=0.5,dtype='int')
def gradient_descent(X_b,y,init_theta,J,dJ,eta=1e-2,max_iters=1e4,break_accuracy=1e-8):
theta = init_theta
cur_iter = 0
while cur_iter < max_iters:
gradient = dJ(X_b,y,theta)
last_theta = theta
theta = theta - eta*gradient
if abs(J(X_b,y,theta)-J(X_b,y,last_theta)) < break_accuracy:
break
cur_iter += 1
return theta
X_train_b = np.hstack([np.ones((X_train.shape[0],1),dtype='float'),X_train])
X_test_b = np.hstack([np.ones((X_test.shape[0],1),dtype='float'),X_test])
init_theta = np.zeros((X_train_b.shape[1],))
print(init_theta.shape)
theta = gradient_descent(X_train_b,y_train,init_theta,logic_J,logic_dJ)
print(theta)
y_predict = logic_pedict(X_test_b,theta)
from sklearn.metrics import accuracy_score
score = accuracy_score(y_test,y_predict)
print(score)
运行结果：
(5,)
[-0.34490434 -0.51879238 -2.05023483 3.05400097 1.36888901]
1.0
8.1.3使用sklearn中的LR
#程序8-2
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
#取出鸢尾花前2个种类
X = X[y<2]
y = y[y<2]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='liblinear')
log_reg.fit(X_train,y_train)
score = log_reg.score(X_test,y_test)
print(log_reg.coef_)
print(log_reg.intercept_)
print(score)
运行结果：
[[-0.36186276 -1.43574562 2.11452526 0.96656658]]
[-0.23774397]
1.0
在sklearn的线性模块中，调用类LogisticRegression就可以使用逻辑回归。参数solver表示优化损失函数的算法，其中liblinear表示使用开源的liblinear库实现，具体是使用坐标轴下降法（并不是梯度下降法）。
LogisticRegression中的具体参数可以参考博客：https://blog.csdn.net/jark_/article/details/78342644
8.2决策边界
对于
，当>=0.5时，
=1；当<=0.5时，=0。我们把=0.5，即Xbθ = 0称为决策边界。
当仅有2个特征的数据集可以表示为y=θ0+θ1*x1+θ2*x2，其决策边界为θ0+θ1*x1+θ2*x2=0，即x2=(-θ0-θ1*x1)/(θ2)，我们尝试绘制它的决策边界。
#程序8-3
import numpy as np
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
iris = datasets.load_iris()
X = iris.data
y = iris.target
#取出鸢尾花前2个种类
X = X[y<2,:2]
y = y[y<2]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='liblinear')
log_reg.fit(X_train,y_train)
print(log_reg.intercept_)
print(log_reg.coef_)
def x2(clf,x1):
return (-clf.coef_[0][0]*x1-clf.intercept_)/clf.coef_[0][1]
x1_boundary = np.linspace(4,8,1000)
x2_boundary = x2(log_reg,x1_boundary)
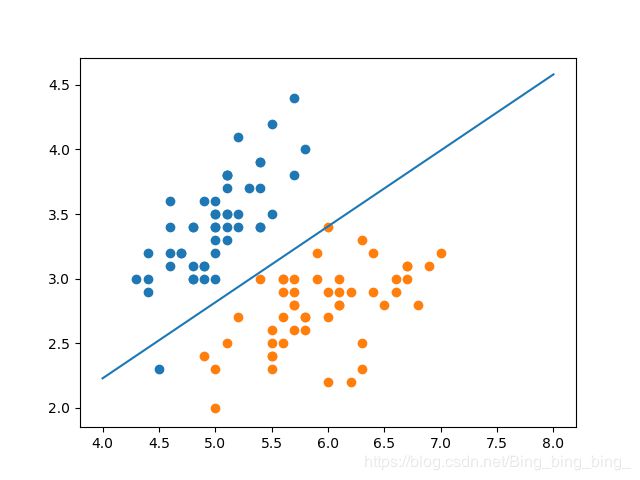
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.plot(x1_boundary,x2_boundary)
plt.show()
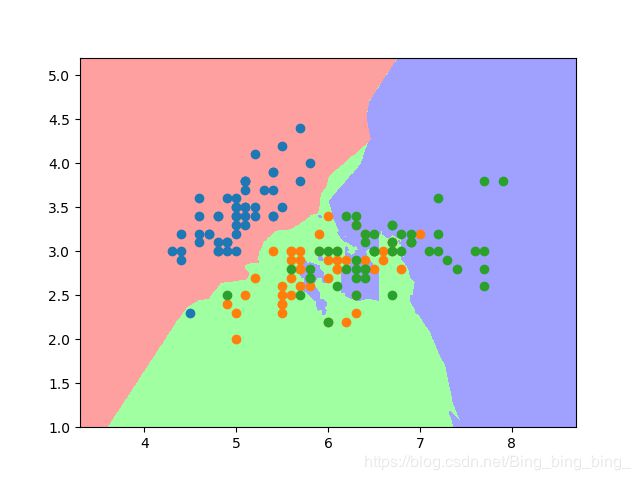
运行结果：
[-0.43008771]
[[ 2.05941418 -3.50276446]]
#程序8-4
import numpy as np
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
iris = datasets.load_iris()
X = iris.data
y = iris.target
#取出鸢尾花前2个种类
X = X[y<2,:2]
y = y[y<2]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
def plot_decision_boundary(clf, X, y, num_row=100, num_col=100):
"""
绘制决策边界
:param clf: 分类器， 即训练后的模型
:param X: 输入的训练数据X
:param y: 输入真实的训练数据y
:param num_row: 单位行数据生成的基本个数
:param num_col: 单位列数据生成的基本个数
"""
#以训练数据集X的第一个特征作为x轴，第二个特征作为y轴，生成坐标轴的间距
sigma = 1 #防止数据在图形的边上而加上的一个偏移量，设定一个较小的值即可
x_min, x_max = np.min(X[:, 0])-sigma, np.max(X[:, 0])+sigma
y_min, y_max = np.min(X[:, 1])-sigma, np.max(X[:, 1])+sigma
#对间距进行等分成t1、t2，并t1按照t2的列数进行行变换、t2按照t1的行数进行列变换
t1 = np.linspace(x_min, x_max, int(x_max-x_min)*num_row).reshape(-1,1)
t2 = np.linspace(y_min, y_max, int(y_max-y_min)*num_col).reshape(-1,1)
x_copy, y_copy = np.meshgrid(t1, t2)
#将变换后的x_，y_生成坐标轴的每个点
xy_all = np.stack((x_copy.reshape(-1,), y_copy.reshape(-1,)), axis=1)
#对坐标轴的点进行预测，并将预测结果变换为对应点的结果
y_predict = clf.predict(xy_all)
y_predict = y_predict.reshape(x_copy.shape)
#设置使用的颜色colors
cm_dark = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0', '#A0A0FF'])
#绘制等高线，x_copy和y_copy种对应的点
#若y_predict为0绘制#FFA0A0，若y_predict为1绘制#A0A0FF，等高线绘制#A0FFA0
plt.contourf(x_copy, y_copy, y_predict,cmap=cm_dark) #绘制底色
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='liblinear')
log_reg.fit(X_train,y_train)
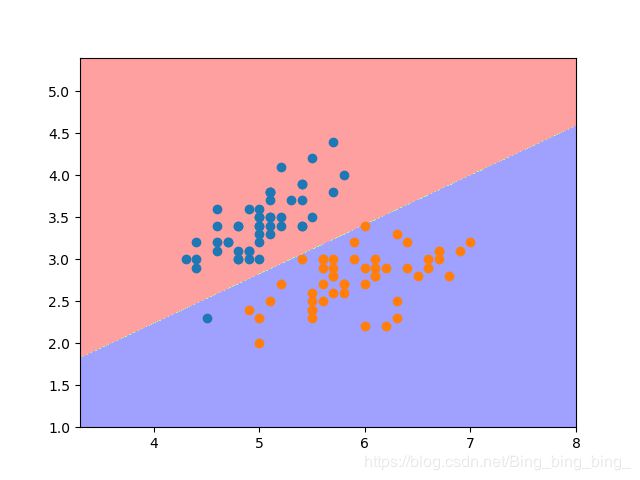
plot_decision_boundary(log_reg,X_train,y_train)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
运行结果：
只要是分类算法，都有决策边界，如kNN。
#程序8-5
import numpy as np
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
iris = datasets.load_iris()
X = iris.data
y = iris.target
#取出鸢尾花前2个种类
X = X[y<2,:2]
y = y[y<2]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
def plot_decision_boundary(clf, X, y, num_row=100, num_col=100):
"""
绘制决策边界
:param clf: 分类器， 即训练后的模型
:param X: 输入的训练数据X
:param y: 输入真实的训练数据y
:param num_row: 单位行数据生成的基本个数
:param num_col: 单位列数据生成的基本个数
"""
#以训练数据集X的第一个特征作为x轴，第二个特征作为y轴，生成坐标轴的间距
sigma = 1 #防止数据在图形的边上而加上的一个偏移量，设定一个较小的值即可
x_min, x_max = np.min(X[:, 0])-sigma, np.max(X[:, 0])+sigma
y_min, y_max = np.min(X[:, 1])-sigma, np.max(X[:, 1])+sigma
#对间距进行等分成t1、t2，并t1按照t2的列数进行行变换、t2按照t1的行数进行列变换
t1 = np.linspace(x_min, x_max, int(x_max-x_min)*num_row).reshape(-1,1)
t2 = np.linspace(y_min, y_max, int(y_max-y_min)*num_col).reshape(-1,1)
x_copy, y_copy = np.meshgrid(t1, t2)
#将变换后的x_，y_生成坐标轴的每个点
xy_all = np.stack((x_copy.reshape(-1,), y_copy.reshape(-1,)), axis=1)
#对坐标轴的点进行预测，并将预测结果变换为对应点的结果
y_predict = clf.predict(xy_all)
y_predict = y_predict.reshape(x_copy.shape)
#设置使用的颜色colors
cm_dark = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0', '#A0A0FF'])
#绘制等高线，x_copy和y_copy种对应的点
#若y_predict为0绘制#FFA0A0，若y_predict为1绘制#A0A0FF，等高线绘制#A0FFA0
plt.contourf(x_copy, y_copy, y_predict,cmap=cm_dark) #绘制底色
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_train)
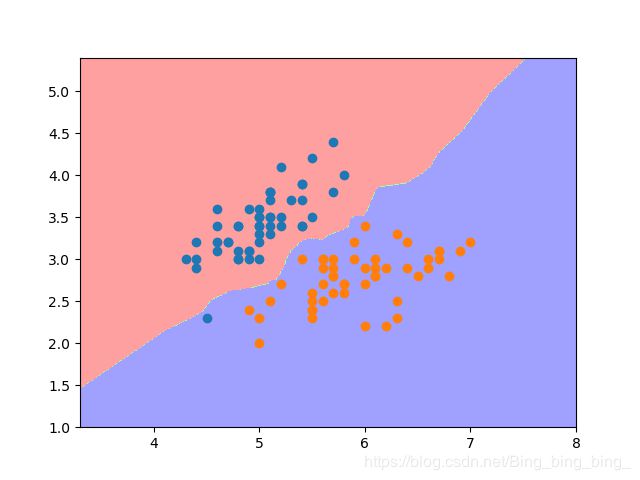
plot_decision_boundary(knn_clf,X_train,y_train)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
运行结果：
前面封装的函数plot_decision_boundary，不仅适用于二分类，也适用于多分类。
#程序8-6
import numpy as np
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
iris = datasets.load_iris()
X = iris.data
y = iris.target
#取出鸢尾花前2个特征
X = X[:,:2]
y = y[:]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
def plot_decision_boundary(clf, X, y, num_row=100, num_col=100):
"""
绘制决策边界
:param clf: 分类器， 即训练后的模型
:param X: 输入的训练数据X
:param y: 输入真实的训练数据y
:param num_row: 单位行数据生成的基本个数
:param num_col: 单位列数据生成的基本个数
"""
#以训练数据集X的第一个特征作为x轴，第二个特征作为y轴，生成坐标轴的间距
sigma = 1 #防止数据在图形的边上而加上的一个偏移量，设定一个较小的值即可
x_min, x_max = np.min(X[:, 0])-sigma, np.max(X[:, 0])+sigma
y_min, y_max = np.min(X[:, 1])-sigma, np.max(X[:, 1])+sigma
#对间距进行等分成t1、t2，并t1按照t2的列数进行行变换、t2按照t1的行数进行列变换
t1 = np.linspace(x_min, x_max, int(x_max-x_min)*num_row).reshape(-1,1)
t2 = np.linspace(y_min, y_max, int(y_max-y_min)*num_col).reshape(-1,1)
x_copy, y_copy = np.meshgrid(t1, t2)
#将变换后的x_，y_生成坐标轴的每个点
xy_all = np.stack((x_copy.reshape(-1,), y_copy.reshape(-1,)), axis=1)
#对坐标轴的点进行预测，并将预测结果变换为对应点的结果
y_predict = clf.predict(xy_all)
y_predict = y_predict.reshape(x_copy.shape)
#设置使用的颜色colors
cm_dark = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0', '#A0A0FF'])
#绘制等高线，x_copy和y_copy种对应的点
#若y_predict为0绘制#FFA0A0，若y_predict为1绘制#A0A0FF，等高线绘制#A0FFA0
plt.contourf(x_copy, y_copy, y_predict,cmap=cm_dark) #绘制底色
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_train)
plot_decision_boundary(knn_clf,X_train,y_train)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
运行结果：
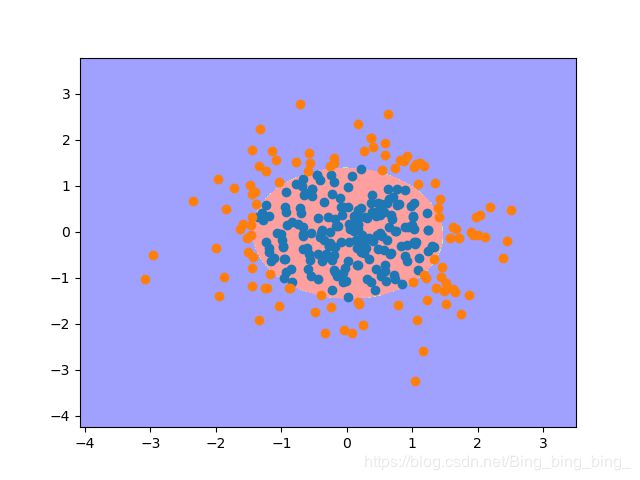
8.3逻辑回归和多项式特征
为了绘制决策边界，使用2个特征的数据集，标签值为0和1。
其中，x1和x2分别表示2个特征。上式表示，当圆心为(0,0)、半径为√2内，y为0；圆外，y为1。
由上式可知，决策边界为
，即
。
#程序8-7
import numpy as np
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
X = np.random.normal(0,1,size=(300,2))
y = np.array((X[:,0]**2+X[:,1]**2)>=2,dtype='int')
print(X.shape)
print(y.shape)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
def plot_decision_boundary(clf, X, y, num_row=100, num_col=100):
"""
绘制决策边界
:param clf: 分类器， 即训练后的模型
:param X: 输入的训练数据X
:param y: 输入真实的训练数据y
:param num_row: 单位行数据生成的基本个数
:param num_col: 单位列数据生成的基本个数
"""
#以训练数据集X的第一个特征作为x轴，第二个特征作为y轴，生成坐标轴的间距
sigma = 1 #防止数据在图形的边上而加上的一个偏移量，设定一个较小的值即可
x_min, x_max = np.min(X[:, 0])-sigma, np.max(X[:, 0])+sigma
y_min, y_max = np.min(X[:, 1])-sigma, np.max(X[:, 1])+sigma
#对间距进行等分成t1、t2，并t1按照t2的列数进行行变换、t2按照t1的行数进行列变换
t1 = np.linspace(x_min, x_max, int(x_max-x_min)*num_row).reshape(-1,1)
t2 = np.linspace(y_min, y_max, int(y_max-y_min)*num_col).reshape(-1,1)
x_copy, y_copy = np.meshgrid(t1, t2)
#将变换后的x_，y_生成坐标轴的每个点
xy_all = np.stack((x_copy.reshape(-1,), y_copy.reshape(-1,)), axis=1)
#对坐标轴的点进行预测，并将预测结果变换为对应点的结果
y_predict = clf.predict(xy_all)
y_predict = y_predict.reshape(x_copy.shape)
#设置使用的颜色colors
cm_dark = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0', '#A0A0FF'])
#绘制等高线，x_copy和y_copy种对应的点
#若y_predict为0绘制#FFA0A0，若y_predict为1绘制#A0A0FF，等高线绘制#A0FFA0
plt.contourf(x_copy, y_copy, y_predict,cmap=cm_dark) #绘制底色
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
def Polynomial_LR(degree):
return Pipeline([
('pol_fea',PolynomialFeatures(degree=degree)),
('std_sca',StandardScaler()),
('LR',LogisticRegression(solver='liblinear'))
])
pol_LR = Polynomial_LR(2)
pol_LR.fit(X_train,y_train)
plot_decision_boundary(pol_LR,X_train,y_train)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
运行结果：
(300, 2)
(300,)
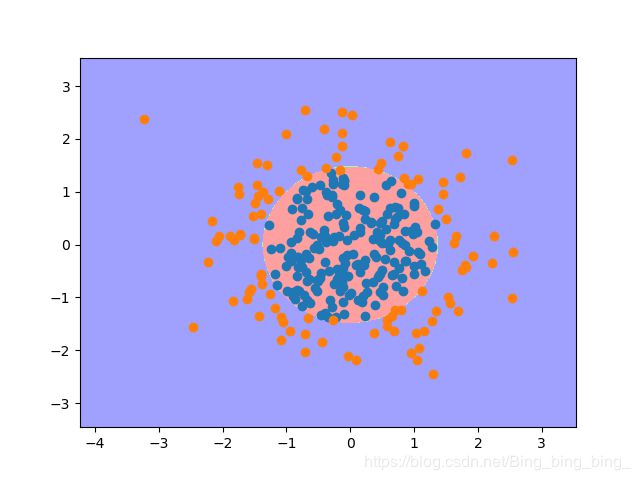
8.4逻辑回归和正则化
在sklearn封装的逻辑回归算法中，linear_model.LogisticRegression类提供正则化的使用。LogisticRegression参数penalty表示正则项，可选参数未’l1’和’l2’，默认为’l2’；参数C表示正则化的超参数，默认为1.0，但它和α不一样的是，C表示损失函数的比例，即：
在前面是α值越大，曲线越平滑；而这里是C越小，曲线越平滑。
#程序8-8
import numpy as np
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
X = np.random.normal(0,1,size=(300,2))
y = np.array((X[:,0]**2+X[:,1]**2)>=2,dtype='int')
print(X.shape)
print(y.shape)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
def plot_decision_boundary(clf, X, y, num_row=100, num_col=100):
"""
绘制决策边界
:param clf: 分类器， 即训练后的模型
:param X: 输入的训练数据X
:param y: 输入真实的训练数据y
:param num_row: 单位行数据生成的基本个数
:param num_col: 单位列数据生成的基本个数
"""
#以训练数据集X的第一个特征作为x轴，第二个特征作为y轴，生成坐标轴的间距
sigma = 1 #防止数据在图形的边上而加上的一个偏移量，设定一个较小的值即可
x_min, x_max = np.min(X[:, 0])-sigma, np.max(X[:, 0])+sigma
y_min, y_max = np.min(X[:, 1])-sigma, np.max(X[:, 1])+sigma
#对间距进行等分成t1、t2，并t1按照t2的列数进行行变换、t2按照t1的行数进行列变换
t1 = np.linspace(x_min, x_max, int(x_max-x_min)*num_row).reshape(-1,1)
t2 = np.linspace(y_min, y_max, int(y_max-y_min)*num_col).reshape(-1,1)
x_copy, y_copy = np.meshgrid(t1, t2)
#将变换后的x_，y_生成坐标轴的每个点
xy_all = np.stack((x_copy.reshape(-1,), y_copy.reshape(-1,)), axis=1)
#对坐标轴的点进行预测，并将预测结果变换为对应点的结果
y_predict = clf.predict(xy_all)
y_predict = y_predict.reshape(x_copy.shape)
#设置使用的颜色colors
cm_dark = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0', '#A0A0FF'])
#绘制等高线，x_copy和y_copy种对应的点
#若y_predict为0绘制#FFA0A0，若y_predict为1绘制#A0A0FF，等高线绘制#A0FFA0
plt.contourf(x_copy, y_copy, y_predict,cmap=cm_dark) #绘制底色
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
def Polynomial_LR(degree,penalty='l2',C=1.0):
return Pipeline([
('pol_fea',PolynomialFeatures(degree=degree)),
('std_sca',StandardScaler()),
('LR',LogisticRegression(penalty=penalty,C=C,solver='liblinear'))
])
pol_LR = Polynomial_LR(20,'l1',0.1)
pol_LR.fit(X_train,y_train)
plot_decision_boundary(pol_LR,X_train,y_train)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
运行结果：
(300, 2)
(300,)
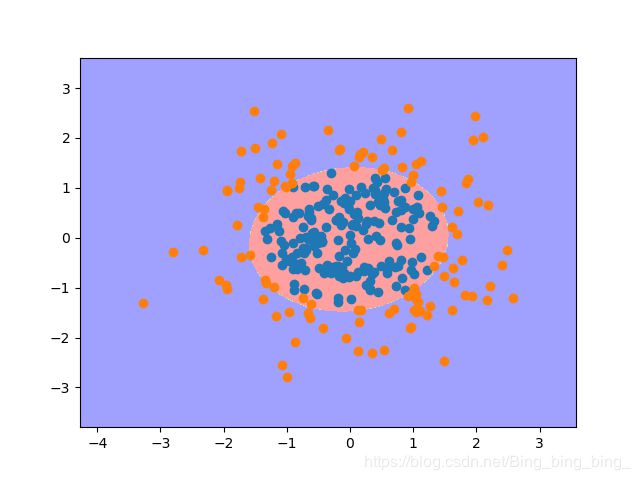
8.5逻辑回归和多分类问题
在在sklearn封装的逻辑回归算法中，linear_model.LogisticRegression类提供对多分类问题的解决，就是OvR、MvM。
OvR：若对数据集进行k分类，则取其中一类如n类是正例，其余都是负类；对这个数据集做k次二分类任务就可以得到对应类别的模型。
MvM：以MvM的特例OvO来讲解，若将数据集进行k分类，取其中2个类别进行训练得到一个模型，一共有k(k-1)/2个分类任务。OvO比OvR更加准确，但计算量也更加高。
LogisticRegression的参数multi_class表示分类方式，可选参数为ovr和multinomial，默认为ovr。若选择了ovr，损失函数优化方法liblinear、newton-cg、lbfgs和sag都可以选择；若选择multinomial，则只能选择newton-cg、lbfgs和sag。
#程序8-9
import numpy as np
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
X = np.random.normal(0,1,size=(300,2))
y = np.array((X[:,0]**2+X[:,1]**2)>=2,dtype='int')
print(X.shape)
print(y.shape)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123456)
def plot_decision_boundary(clf, X, y, num_row=100, num_col=100):
"""
绘制决策边界
:param clf: 分类器， 即训练后的模型
:param X: 输入的训练数据X
:param y: 输入真实的训练数据y
:param num_row: 单位行数据生成的基本个数
:param num_col: 单位列数据生成的基本个数
"""
#以训练数据集X的第一个特征作为x轴，第二个特征作为y轴，生成坐标轴的间距
sigma = 1 #防止数据在图形的边上而加上的一个偏移量，设定一个较小的值即可
x_min, x_max = np.min(X[:, 0])-sigma, np.max(X[:, 0])+sigma
y_min, y_max = np.min(X[:, 1])-sigma, np.max(X[:, 1])+sigma
#对间距进行等分成t1、t2，并t1按照t2的列数进行行变换、t2按照t1的行数进行列变换
t1 = np.linspace(x_min, x_max, int(x_max-x_min)*num_row).reshape(-1,1)
t2 = np.linspace(y_min, y_max, int(y_max-y_min)*num_col).reshape(-1,1)
x_copy, y_copy = np.meshgrid(t1, t2)
#将变换后的x_，y_生成坐标轴的每个点
xy_all = np.stack((x_copy.reshape(-1,), y_copy.reshape(-1,)), axis=1)
#对坐标轴的点进行预测，并将预测结果变换为对应点的结果
y_predict = clf.predict(xy_all)
y_predict = y_predict.reshape(x_copy.shape)
#设置使用的颜色colors
cm_dark = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0', '#A0A0FF'])
#绘制等高线，x_copy和y_copy种对应的点
#若y_predict为0绘制#FFA0A0，若y_predict为1绘制#A0A0FF，等高线绘制#A0FFA0
plt.contourf(x_copy, y_copy, y_predict,cmap=cm_dark) #绘制底色
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
def Polynomial_LR(degree,penalty='l2',C=1.0,multi_class="ovr",solver='liblinear'):
return Pipeline([
('pol_fea',PolynomialFeatures(degree=degree)),
('std_sca',StandardScaler()),
('LR',LogisticRegression(penalty=penalty,C=C,multi_class=multi_class,solver=solver))
])
pol_LR = Polynomial_LR(2,'l2',0.1,'multinomial','newton-cg')
pol_LR.fit(X_train,y_train)
plot_decision_boundary(pol_LR,X_train,y_train)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
运行结果：
(300, 2)
(300,)
