医学图像分割常用的损失函数
本文主要介绍医学图像中常用的损失函数,包括cross entropy, generalized dice coefiicients, focal loss 等。
一、cross entropy 交叉熵
图像分割中最常用的损失函数是逐像素交叉熵损失。该损失函数分别检查每个像素,将类预测(深度方向的像素向量)与我们的热编码目标向量进行比较。
由此可见,交叉熵的损失函数单独评估每个像素矢量的类预测,然后对所有像素求平均值,所以我们可以认为图像中的像素被平等的学习了。但是,医学图像中常出现类别不均衡(class imbalance)的问题,由此导致训练会被像素较多的类主导,对于较小的物体很难学习到其特征,从而降低网络的有效性。
有较多的文章对其进行了研究,包括 Long et al. 的 FCN 在每个通道加权该损失,从而抵消数据集中存在的类别不均的问题。同时,Ronneberger et al.提出的 U-Net 提出了新的逐像素损失的加权方案,使其在分割对象的边界处具有更高的权重。该损失加权方案以不连续的方式帮助他们的 U-Net 模型细分生物医学图像中的细胞,使得可以在二元分割图中容易地识别单个细胞。
二、dice coefficient
dice coefficient 源于二分类,本质上是衡量两个样本的重叠部分。该指标范围从0到1,其中“1”表示完整的重叠。 其计算公式为:
其中 ![]() 表示集合A、B 之间的共同元素,
表示集合A、B 之间的共同元素,![]() 表示 A 中的元素的个数,B也用相似的表示方法。
表示 A 中的元素的个数,B也用相似的表示方法。
为了计算预测的分割图的 dice coefficient,将 ![]() 近似为预测图和label之间的点乘,并将结果函数中的元素相加。
近似为预测图和label之间的点乘,并将结果函数中的元素相加。
因为我们的目标是二进制的,因而可以有效地将预测中未在 target mask 中“激活”的所有像素清零。对于剩余的像素,主要是在惩罚低置信度预测; 该表达式的较高值(在分子中)会导致更好的Dice系数。
为了量化计算 ![]() 和
和 ![]() ,部分研究人员直接使用简单的相加, 也有一些做法是取平方求和。
,部分研究人员直接使用简单的相加, 也有一些做法是取平方求和。
其中,在式子中 Dice系数的分子中有2,因为分母“重复计算” 了两组之间的共同元素。为了形成可以最小化的损失函数,我们将简单地使用1-Dice。这种损失函数被称为 soft dice loss,因为我们直接使用预测概率而不是使用阈值或将它们转换为二进制mask。
关于神经网络输出,分子涉及到我们的预测和 target mask 之间的共同激活,而分母将每个mask中的激活量分开考虑。实际上起到了利用 target mask 的大小来归一化损失的效果,使得 soft dice 损失不会难以从图像中具有较小空间表示的类中学习。
soft dice loss 将每个类别分开考虑,然后平均得到最后结果。
值得注意的是,dice loss比较适用于样本极度不均的情况,一般的情况下,使用 dice loss 会对反向传播造成不利的影响,容易使训练变得不稳定。
三、focal loss
该损失函数在何凯明 1-stage 目标检测框架中被提出。专为解决 class imbalance 问题。首先定性感受一下 target problem(基于目标检测背景):
在目标检测领域,常用的损失函数为CE(cross entropy)。但会带来一些问题:
![]() ,
,
(1)首先,在目标检测中,一般图像的目标所占的比例会远远小于背景,在传统的样本分类中,被分为 positive 和 negative 两类。由于 negative 样本过多,会造成它的loss太大,容易把 positive 的 loss 遮盖从而不利于整个目标函数的收敛,针对这个问题,用平衡的CE (balanced cross entropy)改进传统CE。
![]()
![]() 为权重系数,当为正样本时,
为权重系数,当为正样本时, ![]() ,为负样本时,
,为负样本时,![]()
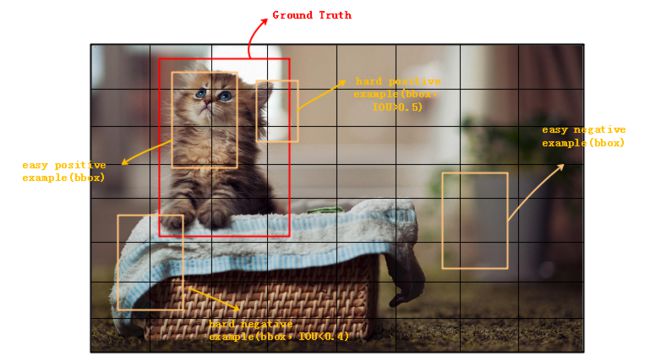
(2)实际上,从图可以看出大多negative 样本位于背景区,而极少的 negative 位于前景和背景的过渡区。位于背景区的样本分类相对容易,成为easy negative, 训练时对应的score很大,loss 相对很小,在计算反向梯度时,造成easy negative example对参数收敛作用有限。从而导致hard negative 样本很难得到更新,效果不佳。
究其原因,是由于常用的损失函数,传统CE(cross entropy)包括平衡化的 CE 均只有 positive/ negative 的区分,未考虑到 easy/ hard 的样本区分。根据文章的分类,有以下几类样本:hard positive(IOU>0.5), easy positive, hard negative(IOU<0.4) 以及 easy negative。
所以提出了focal loss 加大 hard negative的 loss值,使之更好的训练。具体公式如下:
![]()
主要就是增加了 ![]() 这个调节因子。调节因子有两方面作用:1)当网络错分类的时候,
这个调节因子。调节因子有两方面作用:1)当网络错分类的时候,![]() 很小,
很小,![]() ,公式基本不变,但当
,公式基本不变,但当 ![]() 很大,
很大,![]() ,大大降低了 easy example 的损失权重。2)
,大大降低了 easy example 的损失权重。2)![]() ,称为 focusing parameter,
,称为 focusing parameter, ![]() 增强了调节因子的作用。
增强了调节因子的作用。
整体上看,调节因子降低了 easy example 损失的贡献,调节了简单样本权重降低的速率,并拓宽了样本接收低损失的范围。对于困难样本的学习更有利。值得注意的是, ![]() 和调节因子需要配合使用,具体实现时,可以参考论文中的实验进一步探究。
和调节因子需要配合使用,具体实现时,可以参考论文中的实验进一步探究。