【分发糖果】【加密解密】
1.分发糖果
原题地址:https://leetcode-cn.com/problems/candy/solution/fen-fa-tang-guo-by-leetcode/
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
示例 1:
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
思路:
方法 1:暴力法
最简单的方法是使用一个一维的数组 candiescandies 去记录给学生的糖果数。首先我们给每个学生 1 个糖果。然后我们开始从左到右扫描数组。对每一个学生,如果当前的评分 ratings[i]ratings[i] 比前一名学生的评分 ratings[i - 1]ratings[i−1] 高,且 candies[i]<=candies[i - 1]candies[i]<=candies[i−1] ,那么我们更新 candies[i] = candies[i-1] + 1candies[i]=candies[i−1]+1。这样,这两名学生之间的糖果分配目前是正确的。同样的,我们检查当前学生的评分 ratings[i]ratings[i] 是否比 ratings[i+1]ratings[i+1] 高,如果成立,我们同样更新 candies[i]=candies[i+1] + 1candies[i]=candies[i+1]+1 。我们继续对 ratingsratings 数组重复此步骤。如果在某次遍历中, candiescandies 数组不再变化,意味着我们已经得到了最后的糖果分布,此时可以停止遍历。为了记录是否到达最终状态,我们用 flagflag 记录每次遍历是否有糖果数目变化,如果有,则为 True ,否则为False 。
最终,我们可以把 candiescandies 数组中所有糖果数目加起来,得到要求数目最少的糖果数。
代码:
public int candy(int[] ratings) {
int[] candies = new int[ratings.length];
Arrays.fill(candies, 1);
boolean flag = true;
int sum = 0;
while (flag) {
flag = false;
for (int i = 0; i < ratings.length; i++) {
if (i != ratings.length - 1 && ratings[i] > ratings[i + 1] && candies[i] <= candies[i + 1]) {
candies[i] = candies[i + 1] + 1;
flag = true;
}
if (i > 0 && ratings[i] > ratings[i - 1] && candies[i] <= candies[i - 1]) {
candies[i] = candies[i - 1] + 1;
flag = true;
}
}
}
for (int candy : candies) {
sum += candy;
}
return sum;
}
方法 2:用两个数组
算法
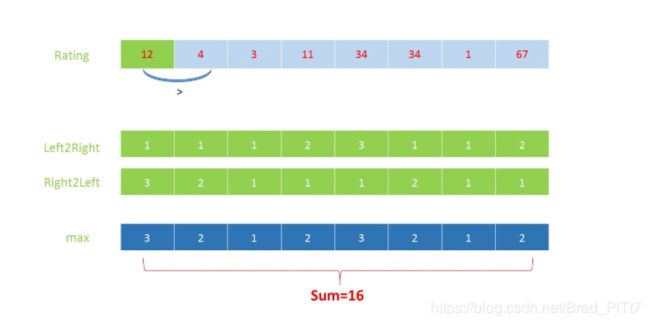
在这种方法中,我们使用两个一维数组 left2rightleft2right 和 right2leftright2left 。数组 left2rightleft2right 用来存储每名学生只与左边邻居有关的所需糖果数。也就是假设规则为:如果一名学生评分比他左边学生高,那么他应该比他左边学生得到更多糖果。类似的,right2leftright2left 数组用来保存只与右边邻居有关的所需糖果数。也就是假设规则为:如果一名学生评分比他右边学生高,那么他应该比他右边学生得到更多糖果。
首先,我们在 left2rigthleft2rigth 和 right2leftright2left 中,给每个学生 1 个糖果。然后,我们从左向右遍历整个数组,只要当前学生评分比他左邻居高,我们在 left2rightleft2right 数组中更新当前学生的糖果数 left2right[i] = left2right[i-1] + 1left2right[i]=left2right[i−1]+1,这是因为在每次更新前,当前学生的糖果数一定小于等于他左邻居的糖果数。
在从左到右扫描后,我们用同样的方法从右到左只要当前学生的评分比他右边(第 (i+1)(i+1) 个)学生高,就更新 right2left[i]right2left[i] 为 right2left[i] = right2left[i + 1] + 1right2left[i]=right2left[i+1]+1 。
现在,对于数组中第 ii 个学生,为了满足题中条件,我们需要给他 \text{max}(left2right[i], right2left[i])max(left2right[i],right2left[i]) 个糖果。因此,最后我们得到最少糖果数:
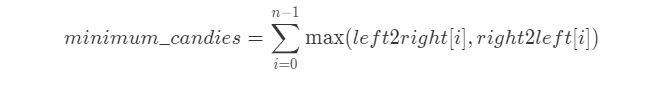
思路转发至leetcode官网:https://leetcode-cn.com/problems/candy/solution/fen-fa-tang-guo-by-leetcode/
public int candy(int[] ratings) {
int []left=new int[ratings.length];
int []right=new int[ratings.length];
int []candys=new int[ratings.length];
// 初始化糖果数组
Arrays.fill(left,1);
Arrays.fill(right,1);
Arrays.fill(candys,1);
for(int i=1;i<ratings.length;i++){
if(ratings[i]>ratings[i-1]&&left[i]<=left[i-1]){
left[i]=left[i-1]+1;
}
}
for(int i=ratings.length-2;i>=0;i--){
if(ratings[i]>ratings[i+1]&&right[i]<=right[i+1]){
right[i]=right[i+1]+1;
}
}
int sum=0;
// 两个数组中找到最大的
for(int i=0;i<candys.length;i++){
candys[i]=Math.max(left[i],right[i]);
sum+=candys[i];
}
return sum;
}
2.加密解密
思路来源于牛客网
现在有一个加密算法是一个字符串(只有01构成的)例如"1001010"加密成"1110100110",每次向右移动一次,一共操作K次,然后将每一个位置对应的0和1进行异或,然后得到加密的字符串。现在假如已知"1001010"需要反求出原始信息字符串"1110100110"
加密过程:

每一列异或,最终结果记录,1110100110 (一共K行)
现在输入N(原始信息串长度),K(加密过程中移动次数),S(加密后的信息串),编写程序求出原始串。
代码:
public static void main(String[] args) {
//String s="1001010";
Scanner sc=new Scanner(System.in);
int N=sc.nextInt();
int K=sc.nextInt();
String S=sc.next();
int []res=new int[N];
int sum=S.charAt(0)=='1'?1:0;
res[0]=sum;
for (int i=1;i<N;i++){
int pre=S.charAt(i-1)=='1'?1:0;
int now=S.charAt(i)=='1'?1:0;
sum=now^pre;
if (i>=K){
sum^=res[i-K];
}
res[i]=sum;
}
StringBuilder sb=new StringBuilder();
for (int t:res){
//System.out.println(t);
sb.append(t);
}
System.out.println(sb.toString());
}

