机器学习试验（二）特征选取

特征选取是机器学习非常重要的内容，俗话说：“特征决定了机器学习效果的上限，算法调参只是逼近这个上限而已”。那么今天就采用数学试验的方法研究特征选取的技巧。包括特征和标签的相关系数，特征噪声的干扰，特征组合产生新特征等的分析。
本次试验：以非线性回归y=sin(x1*x2*2pi)+cos(x3*2pi)为例，研究特征选取对结果的影响。使用lightGBM.LGBMRegressor()算法。

1、基本程序

# -*- coding: utf-8 -*-
""" Created on Thu Jul 26 21:25:42 2018 @author: Administrator """

import numpy as np
import pandas as pd
import math
import lightgbm as lgb
from sklearn import linear_model

def gen_train_test():
    table_train=pd.DataFrame(columns=['x1','x2','x3','y'])
    np.random.seed(0)
    table_train['x1']=np.random.permutation(np.linspace(0,1,10000))
    table_train['x2']=np.random.permutation(np.linspace(0,1,10000))
    table_train['x3']=np.random.permutation(np.linspace(0,1,10000))
    table_train['y']=table_train.apply(lambda x:math.sin(x.x1*x.x2*2*math.pi)+math.cos(x.x3*2*math.pi),axis=1)
    table_test=pd.DataFrame(columns=['x1'])
    table_test['x1']=np.random.rand(10000)
    table_test['x2']=np.random.rand(10000)
    table_test['x3']=np.random.rand(10000)
    return table_train,table_test

def gen_xy(table_train,table_test):
    x_train=table_train.drop(['y'],axis=1)
    x_test =table_test
    y_train=table_train[['y']]
    x_train = np.asarray(x_train)
    y_train = np.asarray(y_train)
    x_test = np.asarray(x_test)
    return x_train,y_train,x_test

def my_RMSE(table_test,y_test):
    table_test['y_test_real']=table_test.apply(lambda x:math.sin(x.x1*x.x2*2*math.pi)+
              math.cos(x.x3*2*math.pi),axis=1)
    table_test['y_test']=y_test
    RMSE=((table_test.y_test_real-table_test.y_test)**2).sum()/len(table_test)
    print('RMSE is %.4f!'%RMSE)
    return RMSE

def lgbR(x_train,y_train,x_test):  
    regr = lgb.LGBMRegressor(num_leaves=32, learning_rate=0.1, n_estimators=160,num_threads=6)
    regr.fit(x_train, y_train)
    y_test = regr.predict(x_test)
    print("Training score:%f"%(regr.score(x_train,y_train)))
    return y_test

table_train,table_test = gen_train_test()
x_train,y_train,x_test = gen_xy(table_train,table_test)
y_test = lgbR(x_train,y_train,x_test)
RMSE = my_RMSE(table_test,y_test)

运行结果：
Training score:0.998166
RMSE is 0.0028!
画出测试集中x1、x2、x3和y_test_real的关系

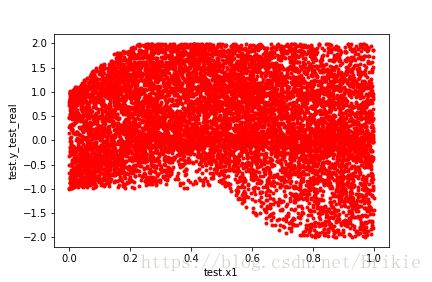
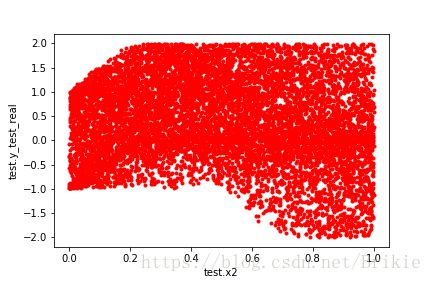
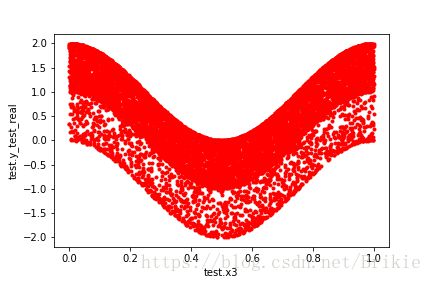
与机器学习试验（一）中的例子相比，本例的非线性程度更高，所以预测误差有所增加，但增加并不多，可见lightGBM是一种很强的非线性学习器。下面开始试验特征选取的效果：

2、特征与标签的相关系数

猜想：与标签相关系数高的特征为重要特征，相关系数低的特征不重要。
计算训练集中x1、x2、x3和y的相关系数

table_train.corr()['y']

Out[108]:
x1 -0.129230
x2 -0.134497
x3 0.006145
y 1.000000
可以看出，各特征与标签y的相关系数都不高，但这些特征都很重要。甚至可以构造出和y相关系数很高，但含有较多噪音而无法预测y的特征来（此处不举例）。
所以，猜想错误。特征与标签的相关系数大小不能说明特征的重要性。

3、重复特征和噪声特征

构造特征x4，使x4=x1，观察是否能够提高预测精度：

def gen_train_test():
    ......
    table_train['x4']=table_train['x1']
    table_test['x4']=table_test['x1']

运行结果为：
Training score:0.998166
RMSE is 0.0028!
结果和原数据集完全一样，可见重复的特征对预测结果没有任何影响。
再构造特征x5，使x5完全随机分布，观察是否降低预测精度：

def gen_train_test():
    ......
    table_train['x5']=np.random.permutation(np.linspace(0,1,10000))
    table_test['x5']=np.random.rand(10000)

运行结果为：
Training score:0.998114
RMSE is 0.0030!
可见，引入和标签完全无关的噪声特征，确实会降低一些预测精度，但由于lightGBM的强大，降低的并不多。

4、特征组合创建新特征

构造x6，使x6=x1*x2

def gen_train_test():
    ......
    table_train['x6']=table_train['x1'].mul(table_train['x2'])
    table_test['x6']=table_test['x1'].mul(table_test['x2'])

运行结果为：
Training score:0.999561
RMSE is 0.0005!
可见，该构造特征的引入极大提高了预测精度。因为该特征包含了标签与原特征数据之间的真实函数关系，所以引入该特征后化简降低了该数据的非线性复杂度，可以提高预测精度。
所以，合理构造特征非线性组合而成的新特征，可有效提高预测精度。
由于并不知道特征和标签之间的实际非线性关系，构造合理的新特征非常困难，构造出无关的新特征反而会一定程度上降低精度。通常应结合数据的实际含义，通过人类理解来构造合理的组合特征，这项工作是现阶段人工智能还远远无法达到的。
（深度神经网络构造合理非线性组合新特征的能力可能非常突出，待以后研究）