Python之常用排序算法(冒泡,选择,插入,快排,二叉树生成以及遍历,堆排,归排,Python的sort及heaqp,python二分查找,)
目录篇:python相关目录篇 点击跳转
目录
- 排序算法
- 一个算法应该具有以下七个重要的特征:
- 算法时间复杂度
- 空间复杂度:
- 实战
- 冒泡排序O(n^2)
- 选择排序O(n^2)
- 插入排序O(n^2)
- 快排排序O(nlog2n) == O(nlogn)
- 二叉树生成以及遍历O(NLOG2N) == O(N*LOGN)
- 堆排序O(nlog2n) == O(nlogn)
- 归并排序O(nlog2n) == O(nlogn)
- Python自带排序sort和sorted内部实现O(nlog2n) == O(nlogn)
- python heapq O(nlog2n) == O(nlogn)
- 二分查找(两种方式:递归和while)
- 计算排序
- top榜单排序
- 所有实验过的排序执行时间对比
排序算法
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
一个算法应该具有以下七个重要的特征:
①有穷性(Finiteness):算法的有穷性是指算法必须能在执行有限个步骤之后终止;
②确切性(Definiteness):算法的每一步骤必须有确切的定义;
③输入项(Input):一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输 入是指算法本身定出了初始条件;
④输出项(Output):一个算法有一个或多个输出,以反映对输入数据加工后的结果。没 有输出的算法是毫无意义的;
⑤可行性(Effectiveness):算法中执行的任何计算步骤都是可以被分解为基本的可执行 的操作步,即每个计算步都可以在有限时间内完成(也称之为有效性);
⑥高效性(High efficiency):执行速度快,占用资源少;
⑦健壮性(Robustness):对数据响应正确。
算法时间复杂度
看别人写算法效率高不高(logn最高,O(1)常数不算):
O(1)>O (log2n) > O(N) >= O (nlog2n)>O(n^2)> O(n^2 +logn)>O(n^3)...>O(n^k)
写算法最少控制在o(n^2) 空间控制在O(1):
空间复杂度:
你的算法使用的空间需要多少,一般情况就是暂用了临时的内存,就算占用也是很少,所以空间复杂度一直是O(1),如果空间复杂度是O(N)等于是复制了一份到内存,根本就没必要
实战
冒泡排序O(n^2)
普通版本
1.列表从第一个元素进行和相邻的元素进行比大,进行互换(大的往右规则互换),接着大的元素继续和后面相邻的元素进行比大,以此类推,最终列表最大的元素放置到了最右边(该次循环结束)
2.继续循环(上次循环得到最大元素切片出来(不包含在列表里面)),然后按照上面的方式继续把该次列表最大的元素放置在最右边
3.以上面方式,最终排序完毕(按照上面的情况每次循环只能提取一个最大的元素放置最右边,那么外层就应该还有个循环是根据列表元素数量的,这样循环套循环最终才排序出来)
详情:看实验(与选择排序(普通版)类似)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random,time
def bubble_sort(array):
for i in range(len(array)):
#array = [3,2,8,1]
#len(array) = 4
#i=0 i=1 i=2
for j in range(len(array)-1-i,):
#len(array)-1-i == 4-1-0 = 3
#j=0 j=1 j=2 j=3
if array[j] > array[j+1]: #array[0] > array[1] == 3 > 2
tmp = array[j] #tmp = 3
array[j] = array[j+1] #array[0] = 2
array[j+1] = tmp #array[1] =3
#第1次大循环的内部循环i=0 range(len(array)-1-i,) == range(3)
#内部循环最终结果 array = [2,3,1,8] 每次内部循环结果会把列表里面最大元素放到最右边
#第2次大循环的内部循环i=1 range(len(array)-1-i,) == range(2)
# 内部循环最终结果 array = [2,1,3,8]
#以此类推最终就排序了
if __name__ == '__main__':
array =[] # [3,2,8,1]
for i in range(50000):
array.append(random.randrange(50000))
#print(array)
time_start = time.time()
bubble_sort(array)
time_end = time.time()
print(array[0:100])
print("cost:",time_end-time_start)
优化版本
1.列表从第一个元素进行和相邻的元素进行比大,大的下标进行标记(此刻不替换)再用标记好的下标元素和其他的元素比大(同理不替换),以此类推找到了列表中最大的元素下标,循环结束,然后把最大元素的下标和该列表最右的元素进行替换位置。
2.继续循环(上次循环得到最大元素切片出来(不包含在列表里面)),然后按照上面的方式继续把该次列表最大的元素放置在最右边
3.以上面方式,最终排序完毕(按照上面的情况每次循环只能提取一个最大的元素放置最右边,那么外层就应该还有个循环是根据列表元素数量的,这样循环套循环最终才排序出来)
详情:看实验(与选择排序(优化版)相反)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random,time
def bubble_sort(array):
for i in range(len(array)):
#array = [3,2,8,1]
#len(array) = 4
#i=0 i=1 i=2
bigess = 0
for j in range(0,len(array)-i):
if array[bigess] < array[j]:
bigess = j
tmp = array[-1-i]
array[-1-i] = array[bigess]
array[bigess] =tmp
if __name__ == '__main__':
array =[] # [871, 100, 160, 755, 614, 621, 403, 671, 256, 915, 174, 906, 253, 973, 199, 370, 950, 970, 287, 648]
for i in range(50000):
array.append(random.randrange(50000))
print(array)
time_start = time.time()
bubble_sort(array)
time_end = time.time()
print(array[0:100])
print("cost:",time_end-time_start)
选择排序O(n^2)
普通版本
1. 列表左边第1个元素进行其他的后面元素进行比小,小的元素替换成为左边第1个的元素,继续和其他的比,以此类推列表左边第一个元素是最小的,该次循环结束
2. 继续循环(上次左边的最小元素被切片了,当做不在列表内),形式如上找到最小的元素放在左边的第一个位置上
3. 按照以上方式最终完成选中排序
详情:看实验(与冒泡排序(普通版)类似)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random,time
def selection_sort(array):
# array = [3,2,8,1]
# len(array) = 4
# i=0 i=1 i=2
for i in range(len(array)):
for j in range(i,len(array)):
if array[i] > array[j]:
tmp = array[i]
array[i] = array[j]
array[j] = tmp
if __name__ == '__main__':
array = []
# array =[871, 100, 160, 755, 614, 621, 403, 671, 256, 915, 174, 906, 253, 973, 199, 370, 950, 970, 287, 648]
for i in range(50000):
array.append(random.randrange(100000))
print(array)
time_start = time.time()
selection_sort(array)
time_end = time.time()
print(array[:100])
print("cost:",time_end-time_start)
优化版本
1.列表左边第1个元素进行其他的后面元素进行比小,小的下标进行标记(此刻不替换)再用标记好的下标元素和其他的元素比小(同理不替换),以此类推找到了列表中最小的元素下标,循环结束,然后把最小元素和该列表最左边的元素进行替换位置。
2.继续循环(上次循环得到最小元素切片出来(不包含在列表里面)),然后按照上面的方式继续把该次列表最小的元素放置在最左边
3.以上面方式,最终排序完毕(按照上面的情况每次循环只能提取一个最小的元素放置最左边,那么外层就应该还有个循环是根据列表元素数量的,这样循环套循环最终才排序出来)
详情:看实验(与冒泡排序(优化版)类似,规则也差不多)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random,time
def selection_sort(array):
for i in range(len(array)):
#array = [3,2,8,1]
#len(array) = 4
#i=0 i=1 i=2
smallest_index = i
for j in range(i,len(array)):
if array[smallest_index] > array[j]:
smallest_index = j
tmp = array[i]
array[i]= array[smallest_index]
array[smallest_index] = tmp
if __name__ == '__main__':
array =[] #[871, 100, 160, 755, 614, 621, 403, 671, 256, 915, 174, 906, 253, 973, 199, 370, 950, 970, 287, 648]
for i in range(50000):
array.append(random.randrange(100000))
print(array)
time_start = time.time()
selection_sort(array)
time_end = time.time()
print(array[:100])
print("cost:",time_end-time_start)
插入排序O(n^2)
for循环从下标1元素开始循环,记录下标1的元素,然后进行while循环,首先下标1跟下标0的元素进行比较,如果比下标0的元素小,那么久把下标0的元素替换到下标1的位置,下标1刚开始被记录的就替换到下标0,因为下标0是边界,所以排序完成
示例:[3,7,12,22,8] x=8
while1: [3,7,12,22,22]
while2:[3,7,12,12,22]
while3:[3,7,7 ,12,22]
停止循环
last [3,7, 7-->x=8,12,22]
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random,time
def insertion_sort(source):
for index in range(1,len(source)):
current_val = source[index] #先记下来每次大循环走到的第几个元素的值
position = index
while position > 0 and source[position-1] > current_val: #当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
source[position] = source[position-1] #把左边的一个元素往右移一位
position -= 1 #只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止
source[position] = current_val #已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
# print(source)
if __name__ == '__main__':
source =[] #[64, 77, 67, 8, 6, 84, 55, 20, 43, 67] #[871, 100, 160, 755, 614, 621, 403, 671, 256, 915, 174, 906, 253, 973, 199, 370, 950, 970, 287, 648]
#[55,64,64,67,77,84] 58
for i in range(50000):
source.append(random.randrange(100000))
# print('list generate done ')
time_start = time.time()
insertion_sort(source)
time_end = time.time()
print(source[:100])
print("cost:",time_end-time_start)
快排排序O(nlog2n) == O(nlogn)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random,time
def quick_sort(array,start,end):
#print("-->",start,end)
if start >=end:
return
k = array[start] #关键K默认下标0的元素
left_flag = start #关键下标默认0
right_flag = end #关键下标默认最后-1
while left_flag < right_flag:
while left_flag < right_flag and array[right_flag] > k: # 代表要继续往左边移动小旗子
right_flag -=1
tmp = array[left_flag]
array[left_flag] = array[right_flag]
array[right_flag] = tmp
#左边小旗子开始向右移动
while left_flag < right_flag and array[left_flag] <= k :
left_flag +=1
#上面的loop一跳出,代表左边小旗子 现在所处的位置的值是比k大的,
tmp = array[left_flag]
array[left_flag] = array[right_flag]
array[right_flag] = tmp
#print(array,left_flag,right_flag)
#开始把问题分半(进行递归)
quick_sort(array,start,left_flag-1)
quick_sort(array,left_flag+1,end)
if __name__ == '__main__':
# array =[64,77,67,8,6,84,55,20,43,67]
array=[]
for i in range(50000):
array.append(random.randrange(100000))
print('list generate done ')
print(array)
time_start = time.time()
quick_sort(array,0,len(array)-1)
time_end = time.time()
print("---->",array[:100])
print("cost:",time_end- time_start)
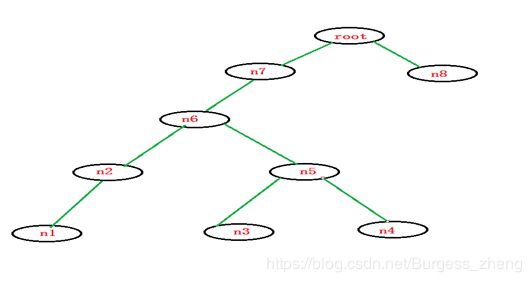
二叉树生成以及遍历O(NLOG2N) == O(N*LOGN)
每个节点都是实例化的对象
前序遍历:根节点->左子树->右子树 root-n7-n6-n2-n1-n5-n3-n4-n8
中序遍历:左子树->根节点->右子树 n1-n2-n6-n3-n5-n4-n7-root-n8
后序遍历:左子树->右子树->根节点 n1-n2-n3-n4-n5-n6-n7-n8-root
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
class TreeNode(object):
def __init__(self,data=0,left=0,right=0):
self.data = data
self.left = left
self.right = right
class BTree(object):
def __init__(self,root=0):
self.root = root
def preOrder(self,treenode):
'''
前序遍历:根节点->左子树->右子树 root-n7-n6-n2-n1-n5-n3-n4-n8
:param treenode:
:return:
'''
if treenode is 0:
return
print(treenode.data)
self.preOrder(treenode.left)
self.preOrder(treenode.right)
def inOrder(self,treenode):
'''
中序遍历:左子树->根节点->右子树 n1-n2-n6-n3-n5-n4-n7-root-n8
:param treenode:
:return:
'''
if treenode is 0:
return
self.inOrder(treenode.left)
print(treenode.data)
self.inOrder(treenode.right)
def postOrder(self,treenode):
'''
后序遍历:左子树->右子树->根节点 n1-n2-n3-n4-n5-n6-n7-n8-root
:param treenode:
:return:
'''
if treenode is 0:
return
self.postOrder(treenode.left)
self.postOrder(treenode.right)
print(treenode.data)
n1 = TreeNode(data=1)
n2 = TreeNode(2,n1,0)
n3 = TreeNode(3)
n4 = TreeNode(4)
n5 = TreeNode(5,n3,n4)
n6 = TreeNode(6,n2,n5)
n7 = TreeNode(7,n6,0)
n8 = TreeNode(8)
root = TreeNode('root',n7,n8)
#上面是实例化成二叉树(笔记用图画出来)
bt = BTree(root)
print("preOrder".center(50,'-'))
print(bt.preOrder(bt.root))
print("inOrder".center(50,'-'))
print (bt.inOrder(bt.root))
print("postOrder".center(50,'-'))
print (bt.postOrder(bt.root))
执行结果
堆排序O(nlog2n) == O(nlogn)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
def sift_down(arr, node, end):
# heap_cycle_one: arr=[2,8,4,7,10,12,6] node=2 end=6
# heap_cycle_two: arr=[2,8,12,7,10,4,6] node=1 end=6
# heap_cycle_three: arr=[2,10,12,7,8,4,6] node=0 end=6
# last_cycle_one: arr=[2,10,6,7,8,4,12] node=0 end=5
root = node#子树节点
# heap_cycle_one: root=2
# heap_cycle_two: root=1
# heap_cycle_three: root=0
# last_cycle_one:root=0
while True:
child = 2 * root + 1 #子树的left子节点
# heap_cycle_one(while_one):child = 5
# heap_cycle_one(while_two): root = 5 child = 11 arr=[2,8,12,7,10,4,6]
# heap_cycle_two(while_one):child = 3
# heap_cycle_two(while_two): root = 4 child = 9 arr=[2,10,12,7,8,4,6]
# heap_cycle_three(while_one):child = 1
# heap_cycle_three(while_two): root=2 child = 5 arr=[12,10,2,7,8,4,6]
# heap_cycle_three(while_three): root=6 child = 13 arr=[2,10,6,7,8,4,12]
# last_cycle_one(while_one):child=1
# last_cycle_one(while_two):root = 1 child=3 arr=[10,2,6,7,8,4,12]
# last_cycle_one(while_three):root = 3 child=7 arr=[10,7,6,2,8,4,12]
if child > end:
# heap_cycle_one(while_one): 5>6 不成立
# heap_cycle_one(while_two): 11>6 成立 结束该次循环 得到 arr=[2,8,12,7,10,4,6]
# heap_cycle_two(while_one):3>6不成立
# heap_cycle_two(while_two): 9>6 成立 结束该次循环 得到 arr=[2,10,12,7,8,4,6]
# heap_cycle_three(while_one):1>6不成立
# heap_cycle_three(while_two): 5>6 不成立
# heap_cycle_three(while_two): 13>6 成立 结束该次循环 得到 arr=[12,10,6,7,8,4,2]
# last_cycle_one(while_one):1>5 不成立
# last_cycle_one(while_two):3>5 不成立
# last_cycle_one(while_three):7>5 成立 结束该次循环 得到 arr=[10,7,6,2,8,4,12]
break
if child + 1 <= end and arr[child] < arr[child + 1]:
# heap_cycle_one(while_one): 6>=6 and 12<6 不成立
# heap_cycle_two(while_one): 4>=6 and 7<10 成立 child=3+1
# heap_cycle_three(while_one): 2>=6 and 10<12 成立 child=1+1
# heap_cycle_three(while_two): 6>=6 and 4<6 成立 child=5+1
# last_cycle_one(while_one):2>=5 and 10<6 不成立
# last_cycle_one(while_two):4>=5 and 7<8 不成立
child += 1
if arr[root] < arr[child]:
# heap_cycle_one(while_one): 4 < 12 成立
# heap_cycle_two(while_one): 8 < 10 成立
# heap_cycle_three(while_one): 2 < 12 成立
# heap_cycle_three(while_two): 2 < 6 成立
# last_cycle_one(while_one):2<10 成立
# last_cycle_one(while_one):2<7 成立
tmp = arr[root]
arr[root] = arr[child]
arr[child] = tmp
# heap_cycle_one(while_one): 下标2的元素和下标5元素替换原 [2,8,4,7,10,12,6] ==> [2,8,12,7,10,4,6]
# heap_cycle_two(while_one): 下标1的元素和下标4元素替换原 [2,8,12,7,10,4,6]==> [2,10,12,7,8,4,6]
# heap_cycle_three(while_one): 下标0的元素和下标2元素替换原 [2,10,12,7,8,4,6]==> [12,10,2,7,8,4,6]
# heap_cycle_three(while_two): 下标2的元素和下标6元素替换原 [12,10,2,7,8,4,6]==> [12,10,6,7,8,4,2]
# last_cycle_one(while_one):下表0的元素和下标1的元素替换原 [2,10,6,7,8,4,12] ==> [10,2,6,7,8,4,12]
# last_cycle_one(while_two):下表1的元素和下标3的元素替换原 [10,2,6,7,8,4,12] ==> [10,7,6,2,8,4,12]
root = child
# heap_cycle_one(while_one): root = 5 [2,8,12,7,10,4,6]
# heap_cycle_two(while_one): root = 4 [2,10,12,7,8,4,6]
# heap_cycle_two(while_one): root = 2 [12,10,2,7,8,4,6]
# heap_cycle_two(while_one): root = 6 [2,10,6,7,8,4,12]
# last_cycle_one(while_one):root = 1 [10,2,6,7,8,4,12]
# last_cycle_one(while_two):root = 3 [10,7,6,2,8,4,12]
else:
# 无需调整的时候, 退出
break
def heap_sort(arr):
'''
完全二叉树的规则:
1最顶的称:根节点
2有子节点的称:子树根节点、也可以是子节点
3没有子节点的称:叶节点
4非叶节点:根节点、子树根节点
5根节点和子树根节点拥有不可超过2个子节点,且有顺序,左子节点到右子节点
堆原理:
1.遵守完全二叉树规则
2.根节点或子树根节点的值 大于或者等于 其左右孩子节点的值 称大顶堆
3.根节点或子树根节点的值 小于或者等于 其左右孩子节点的值 称小顶堆
4.根据子树根节点的下标可以找到该节点的左右子节点
子树根节点 = i
父节点 = i//2 -1
左子节点 = i*2 + 1
右子节点 = i*2+2
堆排序实现逻辑
一.把一个无序的列表变成大顶堆或者小顶堆
一个列表 arr= [2,8,4,7,10,12,6] 是无序的,
所以我们需要该列表的非叶节点:len(arr)//2-1 得到的非叶节点
#非叶子节点 == 根节点 或 子树根节点
非叶节点的作用:通过非叶节点的下标和该下标的前面下标就可以调用整个列表的元素
把列表[2,8,4,7,10,12,6]绘画完全二叉树:图如下:
###############################################
2[下标0]
8[下标1] 4[下标2]
7[下标3] 10[下标4] 12[下标5] 6[下标6]
###############################################
非叶节点 = 2 那么我们就可以通过下标2 1 0的非叶节点可得到整个列表的元素
非叶节点 = 2
2*2+1==5:非叶节点的left子节点
2*2+2==6:非叶节点的right子节点
非叶节点 = 1
1*2+1==3:非叶节点的left子节点
1*2+2==4:非叶节点的right子节点
非叶节点 = 0
0*2+1==1:非叶节点的left子节点
0*2+2==2:非叶节点的right子节点
通过以上把所有的非叶节点和自身的子节点对比以后最大值作为非叶子节点(根或子树根节点)
意味着我们需要从最后的非叶子节点(下标2)进行让其和自身的子节点进行对比,最大值替换到非叶子节点(下标2)
然后往上一层非叶子节点(下标1)进行让其和自身的子节点进行对比,最大值替换到非叶子节点(下标1)
接着往上一层非叶子节点(下标0)进行让其和自身的子节点进行对比,最大值替换到非叶子节点(下标0)
这里我们又需要记住,下标0和其子节点也就是下标1和2进行对比,最大值推到下标0位置
如果下标0的值非常小,和其中的一个子节点最大的值替换了,该子节点如果是子树根节点的话
也必须继续和其子节点对比拿到最大值,以此类推,因为堆原理是所有的非叶节点大于自身的子节点
这样才可以形成堆所有的根节点和子树根节点比自身的子节点大
每次循环必定把一个非叶节点排序完毕,那么意味着有多少个非叶子节点就循环多少次操作(如上循环3次)
执行逻辑:
arr= [2,8,4,7,10,12,6]
###############################################
2[下标0]
8[下标1] 4[下标2]
7[下标3] 10[下标4] 12[下标5] 6[下标6]
###############################################
最后一个非叶节点=len(arr) // 2 – 1
非叶节点分别是:2 1 0
1.从最后一个非叶节点开始
root(非叶节点)=2 arr= [2,8,4,7,10,12,6] list_len=len(arr)-1==6
2.找非叶节点(子树根节点)的左儿子
left = root* 2 +1
left==5
left大于list_len 证明没该左儿子
3.找出非叶节点(子树根节点)的右儿子:
right=root* 2 +2
right = 6
right大于len(arr) 证明没该右儿子
4.子节点之间的比较(arr (left) 和arr (right)进行比大)
arr (left) = arr(5)=12 < arr (right)=arr(6)=6
5.非叶节点(子树根节点)root和right子节点的进行比较:
arr (root) =arr(2)= 4 < arr (right)=arr(5) =12
6.进行替换最大值替换到root节点(下标5替换到下标2)
arr= [2,8,12,7,10,4,6]
#############################################
2[下标0]
8[下标1] 12[下标2]
7[下标3] 10[下标4] 4[下标5] 6[下标6]
#############################################
这样最后的非叶节点的值大于其子节点
被替换的子节点(下标5)也需要进行判断是否是子树根节点
如果是的话也需要进行和自身的子节点进行对比替换 ,以此类推
7.倒数第二个非叶节点(下标1)按照上面步骤1-6相同操作:也就是和自身子节点进行比较替换
进行替换最大值替换到root节点(下标4替换到下标1)
arr= [2,10,12,7,8,4,6]
#############################################
2[下标0]
10[下标1] 12[下标2]
7[下标3] 8[下标4] 4[下标5] 6[下标6]
#############################################
被替换的子节点(下标4)也需要进行判断是否是子树根节点
如果是的话也需要进行和自身的子节点进行对比替换,以此类推
8.假如中间有多个非叶节点,按照上面的操作执行....
9.第一非叶子节点(下标0)按照步骤1-7相同操作:也就是和自身子节点进行比较替换
进行替换最大值替换到root节点(下标2替换到下标0)
arr= [12,10,2,7,8,4,6]
#############################################
12[下标0]
10[下标1] 2[下标2]
7[下标3] 8[下标4] 4[下标5] 6[下标6]
#############################################
被替换的子节点(下标2)也需要进行判断是否是子树根节点
如果是的话也需要进行和自身的子节点进行对比替换 (下标6替换到下标2)
arr= [12,10,6,7,8,4,2]
#############################################
12[下标0]
10[下标1] 6[下标2]
7[下标3] 8[下标4] 4[下标5] 2[下标6]
#############################################
被替换的子节点(下标6)也需要进行判断是否是子树根节点
如果是的话也需要进行和自身的子节点进行对比替换,以此类推
10 最终得到了大顶堆:
arr= [12,10,6,7,8,4,2]
#############################################
12[下标0]
10[下标1] 6[下标2]
7[下标3] 8[下标4] 4[下标5] 2[下标6]
#############################################
二.获得了大顶堆意味根节点和子树根节点绝对比自身的子节点大:如下
#############################################
12[下标0]
10[下标1] 6[下标2]
7[下标3] 8[下标4] 4[下标5] 2[下标6]
#############################################
把顶点(下标0)替换到下标最后:[2,10,6,7,8,4,12],这样最大的值排到最后面
进行切片,把最大值切掉得到新的列表:arr= [2,10,6,7,8,4],根节点值变成了未知大小
#############################################
2[下标0]
10[下标1] 6[下标2]
7[下标3] 8[下标4] 4[下标5]
#############################################
由于我们都知道切片后大顶堆就失效的了意味根节点变成最后下标的值,该值我们未知大小
但是除了根节点(下标0)的值大小我们不清楚以外,子树根节点是一定比自身的子节点大
意味根节点的子节点也就是下标1或者2其中一个肯定是列表最大值
那么我们这次可以从根节点(下标0)顺序让其和自己的子节点(下标1和2进行对比替换最大值)
未知值替换到了下标1或2其中之一,假如下标1被替换了,
那么下标1该子节点如果是子树根节点,也需要和自身的子节点进行对比替换,
不然的话如果该子树根节点如果小于其子节点那么就形参不了大顶堆
而下标2由于没替换,那么自然比其子节点大所以我们可以不用任何操作
执行逻辑:
1.大顶堆的根值和列表最后元素替换后切片得到:
arr= [2,10,6,7,8,4]
#############################################
2[下标0]
10[下标1] 6[下标2]
7[下标3] 8[下标4] 4[下标5]
#############################################
2.虽然根节点值不清楚,但是子树根节点肯定比自身的子节点大,也就是下标1和标2的值肯定比他们子节节点大
我们可以开始进行从下标0的根节点进行和其子节点(下标1 2) 进行对比,继续形成新的大顶堆
3.从根节点开始
root(非叶节点)=0 arr=[2,10,6,7,8,4] list_len=len(arr)-1==5
4.找非叶节点(根节点)的左儿子
left = root* 2 +1
left==1
left大于list_len 证明没该左儿子
5.找出非叶节点(子树根节点)的右儿子:
right=root* 2 +2
right = 2
right大于len(arr) 证明没该右儿子
6.子节点之间的比较(arr (left) 和arr (right)进行比大)
arr (left) = arr(1)=10 < arr (right)=arr(2)=6
7.非叶节点(子树根节点)root和left子节点的进行比较:
arr (root) =arr(0)= 2 < arr (left)=arr(1) =10
8.进行替换最大值替换到root节点(下标1替换到下标0)
arr=[10,2,6,7,8,4]
#############################################
10[下标0]
2[下标1] 6[下标2]
7[下标3] 8[下标4] 4[下标5]
#############################################
被替换的子节点(下标1)也需要进行判断是否是子树根节点
如果是的话也需要进行和自身的子节点进行对比替换 (下标4替换下标1)
arr=[10,8,6,7,2,4]
#############################################
10[下标0]
8[下标1] 6[下标2]
7[下标3] 2[下标4] 4[下标5]
#############################################
被替换的子节点(下标1)也需要进行判断是否是子树根节点
如果是的话也需要进行和自身的子节点进行对比替换 ,以此类推
没被替换的子节点如果是子树根节点那么按照第一次大顶堆他肯定比自身子节点大无需操作
9.此次循环得到大顶堆以后,按照规矩继续和最后一个下标替换然后切片按照1-8步骤重复操作
也就是每次循环可得到一个大顶堆(也就是切片后的列表里最大的值)循环次数大顶堆列表切片后的长度
按上面2个大步骤操作最终排序完毕:[2,4,6,7,8,10,12]
'''
##开始根据原理代码实现 arr=[2,8,4,7,10,12,6]
##第一步骤获取大顶堆
##找到最后的非叶节点
first = len(arr) // 2 -1
# arr=[2,8,4,7,10,12,6] len(arr)=7 7//2-1
# first=2
##最后的非叶节点的数量(其下标到下标0)作为循环的次数
for i in range(first, -1, -1):
# range(2, -1, -1) = [2,1,0]
# heap_cycle_one:i=2
# heap_cycle_two:i=1
# heap_cycle_three:i=0
##顺序从最后一个非叶节点到根节点开始进行和自身的子节点对比替换最大值
##记住非叶节点和其子节点替换以后,替换的子节点如果也是子树根节点,
##那么也需要和自己的子节点对比替换最大值,以此类推得到大顶堆
sift_down(arr, i, len(arr) - 1)
# heap_cycle_one: arr=[2,8,4,7,10,12,6] i=2 7-1=6 得到结果:arr=[2,8,12,7,10,4,6]
# heap_cycle_two: arr=[2,8,12,7,10,4,6] i=1 7-1=6 得到结果:arr=[2,10,12,7,8,4,6]
# heap_cycle_three: arr=[2,10,12,7,8,4,6] i=0 7-1=6 得到结果:arr=[12,10,6,7,8,4,2]
############上面得到了大顶堆 arr = [12,10,6,7,8,4,2]##################
#### 12[下标0] ####
#### 10[下标1] 6[下标2] ####
#### 7[下标3] 8[下标4] 4[下标5] 2[下标6] ####
#大顶堆:所以树根节点比子节点大
##以列表的长度进行循环-1次数进行循环(-1是因为大顶堆最大值替换到最后下标并且切片少了一个元素)
for end in range(len(arr) -1, 0, -1):
# arr=[12,10,6,7,8,4,2] len(arr)=7
# range(7-1, 0, -1) == [6,5,4,3,2,1]
# last_cycle_one: end = 6
# last_cycle_two: end = 5
# last_cycle_three: end = 4
# last_cycle_four: end = 3
# last_cycle_five: end = 2
# last_cycle_six: end = 1
arr[0], arr[end] = arr[end], arr[0]
#进行替换把最大值替换到最后的下标
#last_cycle_one:原arr=[12,10,6,7,8,4,2] ==> arr=[2,10,6,7,8,4,12]
##由于我们都知道切换后大顶堆就失效的了意味根节点变成最后下标的值,该值我们未知大小
##但是除了根节点(下标0)的值大小我们不清楚以外,子树根节点是一定比自身的子节点大
##意味根节点的子节点也就是下标1或者2其中一个肯定是列表最大值
##那么我们这次可以从根节点(下标0)顺序让其和自己的子节点(下标1和2进行对比替换最大值)
##未知值替换到了下标1或2其中之一,假如下标1被替换了,
##那么下标1该子节点如果是子树根节点,也需要和自身的子节点进行对比替换,
##不然的话如果该子树根节点如果小于其子节点那么就形参不了大顶堆
##而下标2由于没替换,那么自然比其子节点大所以我们可以不用任何操作
sift_down(arr, 0, end - 1)
# last_cycle_one: arr=[2,10,6,7,8,4,12] arg[1]=0 arg[2]= 6-1 得到结果:arr=[10,7,6,2,8,4,12]
#last_cycle_one: arr=[4,7,6,2,8,10,12] arg[1]=0 arg[2]= 5-1
#.....
#最终得到结果:arr=[2,8,4,7,10,12,6]
def main():
# [7, 95, 73, 65, 60, 77, 28, 62, 43]
# [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
# l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
# l = [16,9,21,13,4,11,3,22,8,7,15,day27,0]
# array = [16, 9, 21, 13, 4, 11, 3, 22, 8, 7, 15, 29]
array =[] # [871, 100, 160, 755, 614, 621, 403, 671, 256, 915, 174, 906, 253, 973, 199, 370, 950, 970, 287, 648]
for i in range(50000):
array.append(random.randrange(50000))
# for i in range(2,5000):
# #print(i)
# array.append(random.randrange(1,i))
# print(array)
start_t = time.time()
heap_sort(array)
end_t = time.time()
print("cost:", end_t - start_t)
# print(array)
# print(l)
# heap_sort(l)
# print(l)
if __name__ == "__main__":
main()
归并排序O(nlog2n) == O(nlogn)
归并排序:
先分开再合并,分开成单个元素,合并的时候按照正确顺序合并
假如我们有一个n个数的数列,下标从0到n-1
首先是分开的过程
1 我们按照 n//2 把这个数列分成两个小的数列
2 把两个小数列 再按照新长度的一半 把每个小数列都分成两个更小的
。。。一直这样重复,一直到每一个数分开了
比如: 6 5 4 3 2 1
第一次 n=6 n//2=3 分成 6 5 4 3 2 1
第二次 n=3 n//2=1 分成 6 5 4 3 2 1
第三次 n=1的部分不分了
n=2 n//2=1 分成 5 4 2 1
之后是合并排序的过程:
3 分开之后我们按照最后分开的两个数比较大小形成正确顺序后组合绑定
刚刚举得例子 最后一行最后分开的数排序后绑定 变成 4 5 1 2
排序后倒数第二行相当于把最新分开的数排序之后变成 6 4 5 3 12
4 对每组数据按照上次分开的结果,进行排序后绑定
6 和 4 5(两个数绑定了) 进行排序
3 和 1 2(两个数绑定了) 进行排序
排完后 上述例子第一行待排序的 4 5 6 1 2 3 两组数据
5 对上次分开的两组进行排序
拿着 4 5 6 1 2 3两个数组,进行排序,每次拿出每个数列中第一个(最小的数)比较,把较小的数放入结果数组。再进行下一次排序。
每个数组拿出第一个数,小的那个拿出来放在第一位 1 拿出来了, 变成4 5 6 2 3
每个数组拿出第一个书比较小的那个放在下一个位置 1 2被拿出来, 待排序 4 5 6 3
每个数组拿出第一个书比较小的那个放在下一个位置 1 2 3 被拿出来, 待排序 4 5 6
如果一个数组空了,说明另一个数组一定比排好序的数组最后一个大 追加就可以结果 1 2 3 4 5 6
相当于我们每次拿到两个有序的列表进行合并,分别从两个列表第一个元素比较,把小的拿出来,在拿新的第一个元素比较,把小的拿出来
这样一直到两个列表空了 就按顺序合并了两个列表
时间复杂度: 最好最坏都是 O( n log n )
稳定性:稳定
缺点:每次拆分数组都要开心的数组, 每次合并数组都要开新数组,空间复杂度很大
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import time
import random
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
def merge(li, low, mid, high):
"""
merge3:【6】
:param li: [3,2,5,1,6]
:param low: 0
:param mid: 0
:param high: 1
#该次从列表中获取了列表的下标low和high的下标元素进行了比较,小追先追加到tml临时列表
#li[low] = 1 li[high] = 4 追加到 tml列表 tml=[1,4]
#把源列表的相同位置分片以后进行了替换
li = [1,4,5,6,2][0:2] = [1,4] = tml tml复制到li
li = [1,4,5,6,2]
merge2
:param li: [2,3,5,1,6]
:param low:0
:param mid:1
:param high:2
merge7
:param li: [2,3,5,1,6]
:param low:3
:param mid:3
:param high:4
:return:
merge1
:param li: [2,3,5,1,6]
:param low:0
:param mid:2
:param high:4
:return:
"""
i = low
#merge3: i = 0
#merge2:i=0
#merge7:i=3
#merge1:i=0
j = mid + 1
#merge3: j = 1
#merge2: j = 2
#merge7:j=4
#merge1:j=3
ltmp = []
#merge3: ltmp =[]
#merge2: ltmp =[]
#merge7: ltmp = []
#merge1: ltmp = []
while i <= mid and j <= high:
#merge3_one:li: [3,2,5,1,6] i=0 j=1 mid=0 hight=1 ltmp=[] 0<=0 and 1<=1 成立
#merge3_two:[3,2,5,1,6] i=0 j=1+1 mid=0 hight=1 ltmp=[2] 0<=0 and 2<=1 不成立 跳出循环
#merge2_one: li: [2,3,5,1,6] i=0 j=2 mid=1 hight=2 ltmp=[] 0<=1 and 2<=2 成立
# merge2_two: li: [2,3,5,1,6] i=0+1 j=2 mid=1 hight=2 ltmp=[2] 1<=1 and 2<=2 成立
# merge2_three: li: [2,3,5,1,6] i=0+2 j=2 mid=1 hight=2 ltmp=[2,3] 2<=1 and 2<=2 不成立
#merge7_one: li=[2,3,5,1,6] i=3 j=4 mid=3 high=4 ltmp=[] 3<=3 and 4<=4 成立
#merge7_two: li=[2,3,5,1,6] i=3+1 j=4 mid=3 high=4 ltmp=[1] 4<=3 不成立
# merge1_one: li=[2,3,5,1,6] i=0 j=3 mid=2 high=4 ltmp=[] 0<=2 and 3<=4 成立
# merge1_two: li=[2,3,5,1,6] i=0 j=3+1 mid=2 high=4 ltmp=[1] 0<=2 and 4<=4 成立
# merge1_three: li=[2,3,5,1,6] i=+1 j=3+1 mid=2 high=4 ltmp=[1,2] 1<=2 and 4<=4 成立
# merge1_four: li=[2,3,5,1,6] i=0+1+1 j=3+1 mid=2 high=4 ltmp=[1,2,3] 2<=2 and 4<=4 成立
# merge1_five: li=[2,3,5,1,6] i=0+1+1+1 j=3+1 mid=2 high=4 ltmp=[1,2,3,5] 3<=2 and 4<=4 不成立
if li[i] < li[j]:
# merge3_one:li: [3,2,5,1,6] i=0 j=1 hight=1 ltmp=[] 3<2 不成立
# merge2_one: li: [2,3,5,1,6] i=0 j=2 mid=1 hight=2 ltmp=[] 2<5成立
# merge2_two: li: [2,3,5,1,6] i=1 j=2 mid=1 hight=2 ltmp=[5] 3<5 成立
#merge7_one: li=[2,3,5,1,6] i=3 j=4 mid=3 high=4 ltmp=[] 1<6 成立
# merge1_one: li=[2,3,5,1,6] i=0 j=3 mid=2 high=4 ltmp=[] 2<1 不成立
# merge1_two: li=[2,3,5,1,6] i=0 j=3+1 mid=2 high=4 ltmp=[1] 2<6 成立
# merge1_three: li=[2,3,5,1,6] i=+1 j=3+1 mid=2 high=4 ltmp=[1,2] 3<6成立
# merge1_four: li=[2,3,5,1,6] i=0+1+1 j=3+1 mid=2 high=4 ltmp=[1,2,3] 5<6 成立
ltmp.append(li[i])
i += 1
# merge2_one: li: [2,3,5,1,6] i=0+1 j=2 mid=1 hight=2 ltmp=[2]
# merge2_two: li: [2,3,5,1,6] i=1+1 j=2 mid=1 hight=2 ltmp=[2,3] 成立
# #merge7_one: li=[2,3,5,1,6] i=3+1 j=4 mid=3 high=4 ltmp=[1]
# merge1_two: li=[2,3,5,1,6] i=+1 j=3+1 mid=2 high=4 ltmp=[1,2]
# merge1_three: li=[2,3,5,1,6] i=0+1+1 j=3+1 mid=2 high=4 ltmp=[1,2,3]
# merge1_four: li=[2,3,5,1,6] i=0+1+1+1 j=3+1 mid=2 high=4 ltmp=[1,2,3,5]
else:
ltmp.append(li[j])
j += 1
# merge3_one: li: [3,2,5,1,6] i=0 j=1+1 hight=1 ltmp=[2] 继续while循环
# merge1_one: li=[2,3,5,1,6] i=0 j=3+1 mid=2 high=4 ltmp=[1] 继续while循环
while i <= mid:
# merge3_two:[3,2,5,1,6] i=0 j=2 mid=0 hight=1 ltmp=[2] 0<=0 成立
# merge3_three:[3,2,5,1,6] i=1 j=2 mid=0 hight=1 ltmp=[2,3] 1<=0 不成立
# merge2_three: li: [2,3,5,1,6] i=2 j=2 mid=1 hight=2 ltmp=[2,3] 2<=1 不成立
# merge7_two: li=[2,3,5,1,6] i=3+1 j=4 mid=3 high=4 ltmp=[1] 4<=3 不成立
# merge1_five: li=[2,3,5,1,6] i=0+1+1+1 j=3+1 mid=2 high=4 ltmp=[1,2,3,5] 3<=2 不成立
ltmp.append(li[i])
i += 1
# merge3_two:[3,2,5,1,6] i=0+1 j=2 ltmp=[2,3]
while j <= high:
# merge3_three:[3,2,5,1,6] i=1 j=2 hight=1 ltmp=[2,3] 2 <= 1 不成立
# merge2_three: li: [2,3,5,1,6] i=2 j=2 mid=1 hight=2 ltmp=[2,3] 2<=2 成立
# merge2_four: li: [2,3,5,1,6] i=2 j=3 mid=1 hight=2 ltmp=[2,3,5] 3<=2 不成立
# merge7_two: li=[2,3,5,1,6] i=3+1 j=4 mid=3 high=4 ltmp=[1] 4<=4 成立
# merge7_three: li=[2,3,5,1,6] i=3+1 j=4+1 mid=3 high=4 ltmp=[1,6] 5<=4 不成立
# merge1_five: li=[2,3,5,1,6] i=0+1+1+1 j=3+1 mid=2 high=4 ltmp=[1,2,3,5] 4<=4 成立
# merge1_six: li=[2,3,5,1,6] i=0+1+1+1 j=3+1+1 mid=2 high=4 ltmp=[1,2,3,5,6] 5<=4 不成立
ltmp.append(li[j])
j += 1
# merge2_three: li: [2,3,5,1,6] i=2 j=2+1 mid=1 hight=2 ltmp=[2,3,5]
# merge7_two: li=[2,3,5,1,6] i=3+1 j=4+1 mid=3 high=4 ltmp=[1,6] 4<=4 成立
#merge1_five: li=[2,3,5,1,6] i=0+1+1+1 j=3+1+1 mid=2 high=4 ltmp=[1,2,3,5,6]
li[low:high+1] = ltmp
# merge3_three:[3,2,5,1,6] i=1 j=2 mid=0 hight=1 ltmp=[2,3]
#li[low:high+1] == li[0:2] == [3,2] 进行替换 ltmp
# li[low:high+1] = ltmp == [3,2] = [2,3]
#merge3:li=[2,3,5,1,6]
#merge2_four: li: [2,3,5,1,6] i=2 j=3 mid=1 hight=2 ltmp=[2,3,5]
#li[low:high+1] == li[0:3] == [2,3,5] 进行替换 ltmp
# li[low:high+1] = ltmp == [2,3,5] = [2,3,5]
# merge3:li=[2,3,5,1,6]
# merge7_three: li=[2,3,5,1,6] i=3+1 j=4+1 mid=3 high=4 ltmp=[1,6]
# li[low:high+1] == li[3:5] == [1,6] 进行替换 ltmp
# li[low:high+1] = ltmp == [1,6]= [1,6]
# merge3:li=[2,3,5,1,6]
# merge1_six li=[2,3,5,1,6] i=0+1+1+1 j=3+1+1 mid=2 high=4 ltmp=[1,2,3,5,6]
# li[low:high+1] == li[0:4] == [2,3,5,1,6] 进行替换 ltmp
# li[low:high+1] = ltmp == [2,3,5,1,6] = [1,2,3,5,6]
# merge3:li=[1,2,3,5,6]
def _mergesort(li, low, high):
'''
one: 【1】
:param li: [3,2,5,1,6]
:param low: 0
:param high: 4
two: 【2】
:param li: [3,2,5,1,6]
:param low: 0
:param high:2
three: 【3】
:param li: [3,2,5,1,6]
:param low: 0
:param high:1
four: 【4】
:param li:[3,2,5,1,6]
:param low:0
:param high:0
five: 【5】
:param li:[3,2,5,1,6]
:param low:1
:param high:1
six: 【6】
:param li:[2,3,5,1,6]
:param low:2
:param high:1
:return:
'''
if low < high:
######列表左########
#one【1】: 0 < 4 li=[3,2,5,1,6] low=0 high=4
#two 【2】: 0 <2 li=[3,2,5,1,6] low=0 high=2
#three【3】: 0<1 li=[3,2,5,1,6] low=0 high=1
#four【4】: 0 < 0 #不成立 没有return所以默认是none给three【3】
#####列表右########
#five【5】: 1 < 1 #不成立 没有return所以默认是none给three【3】:over
#six【6】: 2 < 2 #不成立 没有return所以默认是none给Two【2】:over
#seven【7】: 3 < 4 #成立 li=[3,2,5,1,6] low=3 high=4
#eight【8】:3<3 #不成立 没有return所以默认是none给sevev【7】
# nine【9】:4<4 #不成立 没有return所以默认是none给sevev【7】
mid = (low + high) // 2
#one【1】: mid=0+4//2=2 li=[3,2,5,1,6] low=0 mid=2 high=4
#two 【2】: mid = 2//2 =1 li=[3,2,5,1,6] low=0 mid=1 high=2
#three【3】: mid = 0+1//2=0 li=[3,2,5,1,6] low=0 mid=0 high=1
#seven【7】: mid = 3+4//2=3 li=[3,2,5,1,6] low=3 mid=3 high=4
_mergesort(li,low, mid)
#one【1】: 调用了 _mergesort(li=[3,2,5,1,6] ,low=0, mid=2) 代号:two【2】 li=[3,2,5,1,6] low=0 mid=2 high=4
#two 【2】: 调用了 _mergesort(li=[3,2,5,1,6] ,low=0, mid=1) 代号:three【3】 li=[3,2,5,1,6] low=0 mid=1 high=2
#three【3】: 调用了 _mergesort(li=[3,2,5,1,6] ,low=0, mid=0) 代号:four【4】 li=[3,2,5,1,6] low=0 mid=0 high=1
#three【3】: 收到了 four【4】的返回值是None,li=[3,2,5,1,6] ,low=0, mid=0 hight=1 往下执行three【3】
# two【2】收到了three【3】的返回值None 但是li=[2,3,5,1,6],low=0, mid=1 hight=2 继续往下执行two【2】
# one【1】: 收到了two【2】的返回值None 但是li=[2,3,5,1,6],low=0, mid=2 hight=4继续往下执行one【1】
# seven【7】: 调用了 _mergesort(li=[2,3,5,1,6] ,low=3, mid=3) 代号:eight【8】li=[2,3,5,1,6] low=3 mid=3 high=4
# seven【7】: 收到了eight【8】的返回值None 但是li=[2,3,5,1,6] low=3 mid=3 high=4 继续往下执行seven【7】
_mergesort(li, mid+1, high)
# three【3】: 执行了 _mergesort(li=[3,2,5,1,6],mid=1,high=1) 代号:five【5】 li=[3,2,5,1,6] low=0 mid=0 high=1
# three【3】: 收到了 five【5】的返回值是None往下执行three【3】
# two 【2】: 执行了 _mergesort(li=[2,3,5,1,6],mid=2,high=2) 代号: six【6】 li=[2,3,5,1,6] low=0 mid=1 high=2
# two 【2】: 收到了 six【6】的返回值是None往下执行 two【2】
# one【1】: 执行了 _mergesort(li=[2,3,5,1,6] ,low=3, mid=4) 代号:seven【7】 li=[2,3,5,1,6] low=0 mid=2 high=4
# seven【7】: 执行了 _mergesort(li=[2,3,5,1,6] ,low=4, mid=4) 代号:nine【9】 li=[2,3,5,1,6]low=3 mid=3 high=4
# seven【7】: 收到了 nine【9】的返回值是None往下执行seven【7】
# one【1】: 收到了seven【7】的返回值None 但是li=[2,3,5,1,6],low=0, mid=2 hight=4继续往下执行one【1】
merge(li, low, mid, high)
# three【3】:执行了 merge(li=[3,2,5,1,6], low=0, mid=0, high=1) 代号:merge3 li=[3,2,5,1,6] low=0 mid=0 high=1
# three【3】执行的merge3 得到了li = [2,3,5,1,6] 返回None给two【2】(开始执行two【2】)
# two 【2】执行了 merge(li=[2,3,5,1,6], low=0, mid=1, high=2) 代号:merge2 : li=[2,3,5,1,6] low=0 mid=1 high=2
# two 【2】执行的merge2 得到了li = [2,3,5,1,6] 返回None给one【1】(开始执行one【1】)
# seven【7】: 执行了 merge(li=[2,3,5,1,6], low=3, mid=3, high=4) 代号:merge7 li=[2,3,5,1,6] low=3 mid=3 high=4
# seven【7】 执行的merge7 得到了li = [2,3,5,1,6] 返回None给one【1】(开始执行one【1】)
# one【1】执行了 merge(li=[2,3,5,1,6], low=0, mid=2, high=4) 代号:merge1 li=[2,3,5,1,6]low=0, mid=2 high=4
# one【1】 执行的merge1 得到了li =[1,2,3,5,6] 整个程序结束
#以此类推,
# 逻辑如下:
#row1:
#li = [3, 2, 5, 1, 6], low = 0, mid = 0, high = 1
#拿到了进行切片得到: li[low:hight+1]== li[0:2] == [3,2]
#从列表[3,2]进行while判断比较元素大小,从小到大顺序追加到临时列表ltmp(简单理解就是:对该列表进行排序)
#得到:ltmp=[2,3]
#然后和li切片出来的列表下标对应进行合并(替换):li[low:hight+1]=ltmp == li[0:2] =[2,3]
#最终得到 :li=[2, 3, 5, 1, 6]
# row2 :
#li = [2, 3, 5, 1, 6], low = 0, mid = 1, high = 2
#拿到了进行切片得到: li[low:hight+1]== li[0:3] == [2,3,5]
# 从列表[2,3,5]进行while判断比较元素大小,从小到大顺序追加到临时列表ltmp(简单理解就是:对该列表进行排序)
#得到:ltmp=[2,3,5]
#然后和li切片出来的列表下标对应进行合并(替换):li[low:hight+1]=ltmp == li[0:3] =[2,3,5]
#最终得到: li=[2, 3, 5, 1, 6]
# row3 :
# li = [2, 3, 5, 1, 6], low = 3, mid = 3, high = 4
# 拿到了进行切片得到: li[low:hight+1]== li[3:5] == [1.6]
# 从列表[1,6]进行while判断比较元素大小,从小到大顺序追加到临时列表ltmp(简单理解就是:对该列表进行排序)
# 得到:ltmp=[1,6]
# 然后和li切片出来的列表下标对应进行合并(替换):li[low:hight+1]=ltmp == li[3:5]=[1,6]
# 最终得到:li=[2, 3, 5, 1, 6]
#row4 :
# li = [2, 3, 5, 1, 6], low = 0, mid = 2, high = 4
# 拿到了进行切片得到: li[low:hight+1]== li[0:5] == [2,3,5,1,6]
# 从列表[2,3,5,1,6]进行while判断比较元素大小,从小到大顺序追加到临时列表ltmp(简单理解就是:对该列表进行合并排序)
# 得到:ltmp=[1,2,3,5,6]
# 然后和li切片出来的列表下标对应进行合并(替换):li[low:hight+1]=ltmp == li[0:5]=[1,2,3,5,6]
# 最终得到 li=[1,2,3,5,6]
return li
@cal_time
def mergesort(li):
'''
:param li:[3,2,5,1,6] 【1】
:return:
'''
_mergesort(li, 0, len(li) - 1)
return li
li = [] # [871, 100, 160, 755, 614, 621, 403, 671, 256, 915, 174, 906, 253, 973, 199, 370, 950, 970, 287, 648]
for i in range(50000):
li.append(random.randrange(50000))
mergesort(li)
Python自带排序sort和sorted内部实现O(nlog2n) == O(nlogn)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random
import time
import copy
import sys
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
@cal_time
def sys_sort(data):
return data.sort()
array =[] # [3,2,8,1]
for i in range(50000):
array.append(random.randrange(50000))
sys_sort(array)
python heapq O(nlog2n) == O(nlogn)
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import heapq
import random
import time
heap = []
data = list(range(10000))
random.shuffle(data) #列表元素打乱
# for num in data:
# heapq.heappush(heap, num)
# # data的元素随机放入heap该列表
# for i in range(len(heap)):
# print(heapq.heappop(heap))
# #提取heap列表里面最小的元素
t1 = time.time()
result = heapq.nsmallest(50000, data)
t2 = time.time()
print('cost:',t2-t1)
print(result)
二分查找(两种方式:递归和while)
1.对列表进行排序
2.计算出列表的长度,
3.通过长度除以2变整数取出列表中间下标的元素
4.要查找的的数字和列表中间的元素进行判断
如果该数字<中间的元素,说明中间元素的后面元素们就不用找了
我们就应该取该列表中间元素的下标-1作为结尾的下标
如果该数字>中间的元素,说明中间元素的前面元素们就不用找了
我们就应该取该列表中间元素的下标+1作为起始的下标
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import time
import random
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
@cal_time
def bin_search(data_set, val):
low = 0
high = len(data_set) - 1
while low <= high:
mid = (low+high)//2
if data_set[mid] == val:
return data_set[mid]
elif data_set[mid] < val:
low = mid + 1
else:
high = mid - 1
return
#装饰器不可以装饰在递归函数
#那么可以使用一种方法就是另起一个函数,接收该递归函数的结果,这样装饰
def binary_search(dataset, find_num):
if len(dataset) > 1:
mid = int(len(dataset) / 2) #该列表中间元素的下标
if dataset[mid] == find_num:
#print("Find it")
return dataset[mid]
elif dataset[mid] > find_num:
return binary_search(dataset[0:mid], find_num)
# 如果该数小于列表中间的元素
# 这里很清楚如果小于中间的元素代表后面的元素就不用查了
# 那么我们只需要把中间元素的下标mid-1作为结尾下标进行递归寻找
else:
return binary_search(dataset[mid + 1:], find_num)
# 如果该数大于于列表中间的元素
# 这里很清楚如果大于中间的元素代表前面的元素就不用查了
# 那么我们只需要把中间元素的下标mid+1最为起始下标进行递归寻找
else:
if dataset[0] == find_num:
#print("Find it")
return dataset[0]
else:
pass
print("Cannot find it.")
#装饰器不可以装饰在递归函数
#那么可以使用一种方法就是另起一个函数,接收该递归函数的结果,这样装饰
@cal_time
def binary_search_alex(data_set, val):
return binary_search(data_set, val)
data = list(range(10000000))
print(bin_search(data, 173320))
print(binary_search_alex(data, 173320))
计算排序
计算排序(场景:随一个区域的人的年龄进行排序,)
场景需要:限定范围(指定的下标>列表最大的元素),且多个元素重复
__author__ = "Burgess Zheng"
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import random
import time
import copy
import sys
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
@cal_time
def sys_sort(data):
return data.sort()
@cal_time
def count_sort(li, max_num):
count = [0 for i in range(max_num + 1)]
#count ==[0.0.0.0.0...]
for num in li:
count[num] += 1
#我们生产的li的列表是有边界的 假如该列表的元素是0-10
#这样num如果是元素5,那么count该列表的下标5的元素+1
#这样如果该li的列表里面有3个5,
#我们后期通过count列表下标5的元素就知道5的次数
i = 0
for num,m in enumerate(count):
#//num下标, m:重复数字的次数
for j in range(m):
li[i] = num
#从下标0开始添加元素
i += 1
data = []
for i in range (50000):
data.append(random.randint(0,100))
print(count_sort(data,100))
data1 = []
for i in range (50000):
data1.append(random.randint(0,100))
print(sys_sort(data1))
top榜单排序
场景(榜单TOP):如微博,新闻等排行榜,要从提取点赞最多的新闻排行榜,或者评论排行榜的前10名or前20名等等...
就需要在某个列表中取出排序最小的10个元素(等于点赞最多的)形成一个新的列表(排序完毕),其他的元素无需理会(不管是否有排序)
import random
import time
import copy
import sys
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
###############Python自带排序###################
@cal_time
def sys_sort(data):
return data.sort()
######################################
#######题目#####################################
#现在又n个数(n>10000),设计算法,按大小顺序排序后,我们只需要得到前面0-9的下标元素,其余不要
##############################################################
##############O(n)方案############################
#示例演变:得到li列表排序好的前3个元素,其余元素排序不排序不理会
#1. li = [1,3,5,4,2,7,9,6,8]
#2. top = [1,3,5,4] 提取了li列表的前4个元素形成top列表
#对top列表使用插入排序 得到 top = [1,3,4,5]
#3. top[3] = li[4] top[3] = 2 top=[1,3,4,2]
# 对top列表使用插入排序 得到 top = [1,2,3,4]
#按照上面这种方式,不断的把li的元素进行替换top列表执行插入排序
#直到li的元素全被替换完毕,结果自然就出来,我们也得到了前面4个排序好的元素(切片取前3个)
#简单的来说:
#1从真正的列表提取前面11个元素形成临时列表,对临时列表进行插入排序
#2.真正列表只需要进行循环从12个元素开始替换掉临时列表的第11个元素
#3.临时列表第11个元素被替换就执行一次插入排序(排序11个元素的列表)
#4.最终临时列表得到了真正列表所有元素排序过后的11个最小的元素,那么提取前10个元素就OK了
def insert(li, i):
'''
row1
:param li: [1,5,2,4]
:param i: 1
row2
:param li: [1,5,2,4]
:param i: 2
row3
:param li: [1,5,2,4]
:param i: 3
'''
tmp = li[i]
j = i - 1
while j >= 0 and li[j] > tmp:
li[j + 1] = li[j]
j = j - 1
li[j + 1] = tmp
def insert_sort(li):
'''
:param li: [1,5,2,4]
:return:
'''
for i in range(1, len(li)): #range(1, len(li)) == [1,2,3]
insert(li, i) #调用 insert ([1,5,2,4],1) #得到了li = [1,5,2,4]
#调用 insert ([1,5,2,4],2) #得到了li = [1,2,5,4]
# 调用 insert ([1,5,2,4],3) #得到了li = [1,2,4,5]
@cal_time
def topk(li, k):
'''
假设
:param li: [1,5,2,4,3]
:param k: 3 #获取排序完毕前3个元素
:return:
'''
top = li[0:k + 1] #[1,5,2,4] ,为什么要4个,是预留后面排序中插入到前面的元素,
insert_sort(top) #调用insert_sort该函数 得到 top = [1,2,4,5]
for i in range(k+1, len(li)): #range(k+1, len(li) == range(4,len(1,5,2,4,3)) == [4,5]
top[k] = li[i] #top[3] = li[4] == top = [1,2,4,3]
insert(top, k) #重新开始排序得出前3位
return top[:-1]
####################################################
####堆的方案##########################################
def sift(data, low, high):
'''
根据完全二叉树堆的原理,通过非叶子节点最终把列表元素最大的替换到列表的下标0
#示例演变:得到li列表排序好的前4个元素,其余元素排序不排序不理会
#1. li = [1,5,7,4,3,8,2,0]
#2. heap=[1,5,7,4,3] 提取了li列表的前5个元素形成heap列表
#对heap列表使用堆排序(列表最大的元素替换到下标 0)
#3. 条件如果 heap[0]>li[5]才执行heap[0] =li[5] 替换li第6个元素(等于把heap最大的元素扔掉)
(循环整个li列表下标了5开始到结尾)
每替换heap一个大元素就进行对heap列表使用堆排序
以此类推最终:循环最终heap该列表得到了最小的5个元素
#4 在遍历heap该列表,让其进行排序(元素小的往前面)
#简单的来说:
#1从真正的列表提取前面10个元素形成临时列表,进行对该临时列表进行堆排序,先对临时列表变成大顶堆(下标0元素最大)
#2.真正列表只需要进行循环从12个元素开始到结尾每次判断元素否小于临时列表的下标0该元素吗,小就替换
#3.临时列表的下标0元素被替换以后就不在是大顶堆了,如果继续堆排序成为大顶堆,如此循环到真正列表元素结束为止
#4.最终临时列表获取到了最小的5个元素,我们在进行堆排序头尾替换循环遍历对该列表进行排序
row1:
:param data: [1,5,7,4,3]
:param low: 1
:param high: 4
row2:
:param data: [1,5,7,4,3]
:param low: 0
:param high: 4
:return:
'''
i = low #非叶子节点(子树)
# row1:i=1
# row2: i=0
j = 2 * i + 1 #左孩子
#row1: j=3
#row2: j=1
tmp = data[i]
# row1: tmp=5
# row2: tmp=1
while j <= high:
#row1: 3<= 4 成立
#row2: 1<= 4 成立
#row2_while j=5 <= 4 不成立 执行结束 data = [7,5,1,4,3]
if j + 1 <= high and data[j] < data[j+1]:
#row1: j+1 = 4:右孩子 4<=4 and 4 < 3 不成立
#row2: j+1 = 2 :右孩子 2<=4 and 5 < 7 成立
j += 1 #j指向右孩子
# row2: j+1 = 2 :右孩子
if data[j] > tmp:
#row1: 4>5不成立
#row2: j=2 7>1 成立
data[i] = data[j] #孩子填到父亲的空位上
# row2: data[i] = 1 替换成 7 data[i] =7 data = [7,5,1,4,3]
# while1: data = [5,4,7,1,3]
i = j
#row2:j成为了非叶子节点 i = 2
j = 2 * i +1
#row0:新左孩子3 j=5
#row2_while1循环
else:
break
data[i] = tmp #最高领导放到父亲位置
@cal_time
def topn(li, n):
'''
假设
:param li: [1,5,7,4,3,8,2,0]
:param n: 5 #获取排序完毕前4个元素
:return:
'''
heap = li[0:n] #heap=[1,5,7,4,3]
#该循环负责吧指定列表进行完全二叉树堆排序最大的元素替换到列表的下标0位置
for i in range(n // 2 - 1, -1, -1): #==for i in [1,0] #1为非叶子节点(子树)
sift(heap, i, n - 1) # row1: sift([1,5,7,4,3],1,4) 获取到 heap = [1,5,7,4,3]
#row2: sift([1,5,7,4,3],0,4) 获取到 heap = data = [7,5,1,4,3]
#遍历
for i in range(n, len(li)): #5,8 == for i in [5,6,7]
if li[i] < heap[0]:
# row1: li[5]=8 < heap[0]=7 不成立
# row2: li[6]=2 < heap[0]=7 成立
# row3: [5,2,1,4,3] li[7]=0 < heap[0]=5 成立
heap[0] = li[i]
# row2: heap = [2,5,1,4,3] li=[2,5,7,4,3,8,7,0]
# row3: heap = [0,2,1,4,3] i=[0,5,7,4,3,8,7,5]
sift(heap, 0, n - 1)
# row2: sift([2,5,1,4,3],0,4) 获取到:heap = [5,2,1,4,3]
# row3:sift([0,5,1,4,3],0,4) 获取到:heap = [4,0,1,2,3]
for i in range(n - 1, -1, -1): # i指向堆的最后 [4,3,2,1,0]
heap[0], heap[i] = heap[i], heap[0] # 领导退休,刁民上位
#heap = [4, 0, 1, 2, 3] heap[0]和heap[4]互换位置 [3,0,1,2,4]
#row2:heap = [3,2,1,0,4] heap[0]和heap[3]互换位置 [0,2,1,3,4]
#row3:heap = [2,0,1,3,4] heap[0]和heap[2]互换位置 [1,0,2,3,4]
# row4:heap = 1,0,2,3,4] heap[0]和heap[2]互换位置 [0,1,2,3,4]
sift(heap, 0, i - 1) # 调整出新领导
# row2: sift( [3,0,1,2,4] , 0, 4 - 1) 获取到:heap = [3,2,1,0,4]
# row3: sift( [0,2,1,3,4] , 0, 3- 1) 获取到:heap = [2,0,1,3,4]
# row4: sift( [1,0,2,3,4] , 0, 2 -1) 获取到:heap = [1,0,2,3,4]
# row5... 1
# row6... 0
#最终得到了heap = [0,1,2,3,4]
return heap
############################################################
####################测试3种排序###############################
data0 = list(range(50000))
random.shuffle(data0)
print(topk(data0,10))
data1 = list(range(50000))
random.shuffle(data1)
print(topn(data1, 10))
data2 = list(range(50000))
random.shuffle(data2)
sys_sort(data2)
print(data2[0:10])
所有实验过的排序执行时间对比
冒泡排序O(n^2):50000个元素排序时间:574.2363秒(时间跟机器性能有关,该测试只限本机器)
冒泡排序优化版O(n^2):50000个元素排序时间:212.2070秒(时间跟机器性能有关,该测试只限本机器)
选择排序O(n^2):50000个元素排序时间:357.8232秒(时间跟机器性能有关,该测试只限本机器)
选择排序优化版O(n^2):50000个元素排序时间:214.9414秒(时间跟机器性能有关,该测试只限本机器)
插入排序O(n^2):50000个元素排序时间:331.9482秒(时间跟机器性能有关,该测试只限本机器)
快速排序O(nlog2n):50000个元素排序时间:0.4804秒(时间跟机器性能有关,该测试只限本机器)
堆排序O(nlog2n):50000个元素排序时间:0.8320秒(时间跟机器性能有关,该测试只限本机器)
归并排序O(nlog2n):50000个元素排序时间:0.5224秒(时间跟机器性能有关,该测试只限本机器)
python系统自带sort排序O(nlog2n):50000个元素排序时间:0.0263秒秒(时间跟机器性能有关,该测试只限本机器)
python系统自带heapq排序O(nlog2n):50000个元素排序时间:0.0283秒(时间跟机器性能有关,该测试只限本机器)
-------------------------------------------------------------------------------------
(场景:统计区域所有人的年龄)
【需求:限定范围(指定的下标>列表最大的元素),且多个元素重复..】:
计算排序O(nlog2n)50000随机元素:100以内的数字列表跑的时间和Python自带排序对比:0.0146秒(时间跟机器性能有关,该测试只限本机器)(列表里面越多元素重复那么对Python自带sort排序有那么点优势,如果列表没有重复元素情况下和Python字典的sort排序比较..那效率低太多了)
--------------------------------------------------------------------------------------
场景(榜单TOP):如微博,新闻等排行榜,要从提取点赞最多的新闻排行榜,或者评论排行榜的前10名or前20名等等...
就需要在某个列表中取出排序最小的10个元素(等于点赞最多的)形成一个新的列表(排序完毕),其他的元素无需理会(不管是否有排序)
topk提取(使用插入排序))O(n):50000个元素排序时间: 0.0419秒
topn提取(使用堆排序)O(n): 50000个元素排序时间: 0.0097秒
Python自带sort排序O(nlogn): 50000个元素排序时间: 0.0263秒
Python自带heapq排序O(n): 50000个元素排序时间: 0.0048秒
(时间跟机器性能有关,该测试只限本机器)
目录篇:python相关目录篇 点击跳转