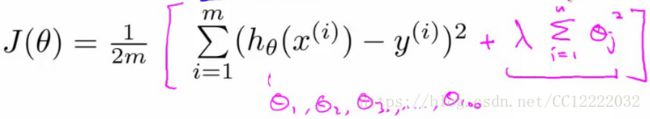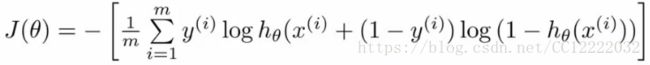吴恩达机器学习总结：第四课 正则化（大纲摘要及课后作业）

为了更好的学习，充分复习自己学习的知识，总结课内重要知识点，每次完成作业后

都会更博。

英文非官方笔记

总结

1.过拟合问题

    （1）线性回归的过拟合

        a .过拟合导致高方差，欠拟合导致高偏差

        b.泛化能力差

    （2）逻辑回归的过拟合

    （3）解决过拟合方法

      a.减少特征数量（会造成信息缺失）

        b.正则化

2.正则化的代价函数优化

    （1）代价函数（其中正则想不包括θ0）

    （2）正则化参数λ

      a.控制我们两个目标之间的权衡（拟合训练集很好、保持参数小）

        b.如果λ太大，就会过度惩罚，导致参数接近0

3.正则化的线性回归

    （1）梯度下降

 4.正则化的正规方程

4.正则化的逻辑回归

（1）代价函数

（2）梯度下降

作业

（1）可视化

data = load('ex2data2.txt');
X = data(:, [1, 2]); y = data(:, 3);
plotData(X, y);
hold on;
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
legend('y = 1', 'y = 0')
hold off;

（2）正则化逻辑回归

X = mapFeature(X(:,1), X(:,2));
%初始化参数
initial_theta = zeros(size(X, 2), 1);
lambda = 1;
[cost, grad] = costFunctionReg(initial_theta, X, y, lambda);
% theta为1 λ为10
test_theta = ones(size(X,2),1);
[cost, grad] = costFunctionReg(test_theta, X, y, 10);

%costFunctionReg函数
m = length(y);
J = 0;
grad = zeros(size(theta));
theta_1 = [0;theta(2:end)];
J =(-1/m)*sum( y.*log(sigmoid(X *theta)) + (1 - y).*log(1 - sigmoid(X*theta)) ) + 1/(2*m)*lambda*theta_1' *theta_1;
grad = ( X' * (sigmoid(X*theta) - y ) )/ m + lambda/m * theta_1 ;
end

（3）正则化和准确度

initial_theta = zeros(size(X, 2), 1);
lambda = 100;
options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, J, exit_flag] = ...
	fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);
plotDecisionBoundary(theta, X, y);
hold on;
title(sprintf('lambda = %g', lambda))
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
legend('y = 1', 'y = 0', 'Decision boundary')
hold off;
p = predict(theta, X);

%决策边界函数
plotData(X(:,2:3), y);
hold on
if size(X, 2) <= 3
    % Only need 2 points to define a line, so choose two endpoints
    plot_x = [min(X(:,2))-2,  max(X(:,2))+2];
    % Calculate the decision boundary line
    plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));
    % Plot, and adjust axes for better viewing
    plot(plot_x, plot_y)
    % Legend, specific for the exercise
    legend('Admitted', 'Not admitted', 'Decision Boundary')
    axis([30, 100, 30, 100])
else
    % Here is the grid range
    u = linspace(-1, 1.5, 50);
    v = linspace(-1, 1.5, 50);
    z = zeros(length(u), length(v));
    % Evaluate z = theta*x over the grid
    for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z'; % important to transpose z before calling contour
    contour(u, v, z, [0, 0], 'LineWidth', 2)
end
hold off
end

&预测函数
m = size(X, 1); % Number of training examples
p = zeros(m, 1);
k = find(sigmoid(X *theta)>= 0.5);
p(k) = 1;

%sigmoid函数
g = zeros(size(z));
g = 1./(1 + exp(-z));
end