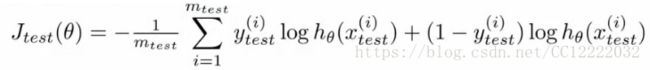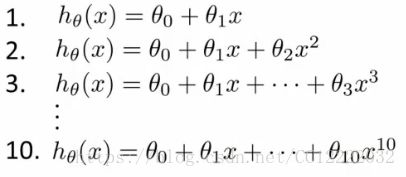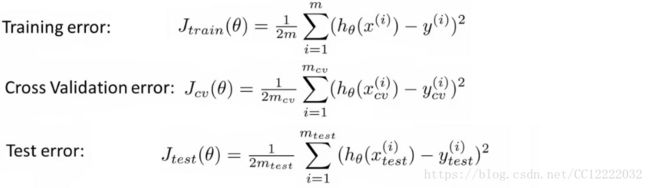吴恩达机器学习总结：第七课 运用机器学习的建议（大纲摘要及课后作业）

为了更好的学习，充分复习自己学习的知识，总结课内重要知识点，每次完成作业后都会更博。

英文非官方笔记

总结

1.决定接下来该怎么尝试

（1）调试学习算法（当实施正则化线性回归之后，预测中有比较大错误）

    a.获得更多训练数据（前提是要保证更多的训练集有用）

    b.使用更小的特征集（仔细选择小子集，或者使用PCA降维）

    c.增加额外的特征（有时候并不有用，你需要关注数据本身，需要消耗很多时间）

    d.增加多项式特征（你这是抓住最后一根稻草）

    e.建立你自己的、新的、更好的特征，在你对于问题的理解的基础上（可能增加无关特征）

    f.尝试增大或者缩小λ

（2）以上步骤可能会浪费你很多时间，所以有一些简单的技术帮助你节省时间

（3）机器学习诊断

    a.一些可以实施来判断是否对算法有益处的测试

    b.观测改变什么可以提高算法性能

    c.需要时间去实施和理解

 2.评估一个假设

（1）标准的评估一个假设方法

    a.将数据分为两部分（训练集和测试集）

    b.典型的拆分方法时7:3（训练集：测试集，此时应该使用分层随机抽样）

（2）因此，一个典型的训练和测试计划为：

    a.从训练集中学习参数θ，用训练集（70%的数据）来最小化代价函数J(θ)

    b.计算测试误差

（3）如果我们用逻辑回归

    a.同样的，测试误差表示为：

    b.有时候会有更好的表示方法（错误分类）

    c.因此，测试误差表示为：

3.模型选择和训练验证测试集

（1）如何选取正则化参数或者多项式维度（模型选择问题）

（2）多项式维度选择

    a.选择不同维度多项式来拟合数据

    b.计算Jtest(θ1)......Jtest(θ10)，比较大小，选择最小的项

（3）改进的模型选择

    a.将训练集划分为3部分（训练集60%，交叉验证集20%，测试集20%）

    b.计算训练误差，交叉验证误差，测试误差

    c.选择检查验证误差最小的项来决定模型阶次

    d.用测试集来预测泛化能力

4.诊断-偏差vs方差

（1）如果你的结果不好，是因为：

    a.高偏差--欠拟合

    b.高方差--过拟合

（2）需要弄清问题才能帮助你提高算法

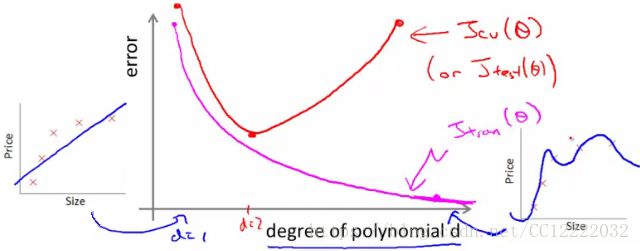
（3）训练误差，交叉验证误差与阶次关系

    a.阶次太小造成高偏差问题（训练和交叉验证误差都很高）

    b.阶次太大造成高方差问题（训练误差低，交叉验证误差高）

5.正则化和偏差/误差

（1）正则化的线性回归

    a.λ太大会造成高偏差，欠拟合（对θ惩罚太严重）

    b.λ太小会造成高方差，过拟合（对θ惩罚力度太小）

（2）选择λ

    a.λ = 0,0.01,0.02.......10，以2的倍次分别代入模型，计算并比较交叉验证误差

    b.当λ很小时，训练误差很小；λ很大时，训练误差很大，此时有很大偏差

    c.当λ很小时，方差很大，过拟合；λ很大时，交叉验证误差很大，此时有很大偏差

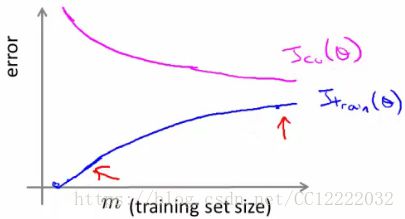
6.学习曲线

（1）高偏差

    a.更多数据不会提高高偏差算法性能

（2）高方差

    a.更多数据对于高偏差问题有帮助

7.下一步做法（回顾）

（1）更多样本--帮助高偏差问题（但是已经高偏差时候无用）

（2）更小特征集--帮助高偏差问题（但是已经高偏差时候无用）

（3）增加额外特征--帮助高偏差问题（因为假设太简单，让假设更难）

（4）增加多项式项数--帮助高偏差问题

（5）减小λ--帮助高偏差；增大λ--帮助高方差

作业

1.载入数据及可视化

clear ; close all; clc load ('ex5data1.mat'); m = size(X, 1); plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5); xlabel('Change in water level (x)'); ylabel('Water flowing out of the dam (y)');

2.代价函数及梯度下降

theta = [1 ; 1]; J = linearRegCostFunction([ones(m, 1) X], y, theta, 1); [J, grad] = linearRegCostFunction([ones(m, 1) X], y, theta, 1); %函数定义 m = length(y); % number of training examples J = 0; grad = zeros(size(theta)); theta_1 = [0;theta(2:end)]; J = sum((X * theta - y).^2) / (2*m) + lambda/(2*m)*theta_1'*theta_1; grad = (1/m)*(X'*( X*theta - y)) + (lambda/m)*theta_1; grad = grad(:); end 

3.训练线性回归

lambda = 0; [theta] = trainLinearReg([ones(m, 1) X], y, lambda); plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5); xlabel('Change in water level (x)'); ylabel('Water flowing out of the dam (y)'); hold on; plot(X, [ones(m, 1) X]*theta, '--', 'LineWidth', 2) hold off; %trainLinearReg函数 initial_theta = zeros(size(X, 2), 1);  costFunction = @(t) linearRegCostFunction(X, y, t, lambda); options = optimset('MaxIter', 200, 'GradObj', 'on'); theta = fmincg(costFunction, initial_theta, options); end 

4.线性回归的学习曲线

lambda = 0; [error_train, error_val] = ... learningCurve([ones(m, 1) X], y, ... [ones(size(Xval, 1), 1) Xval], yval, ... lambda); plot(1:m, error_train, 1:m, error_val); title('Learning curve for linear regression') legend('Train', 'Cross Validation') xlabel('Number of training examples') ylabel('Error') axis([0 13 0 150]) for i = 1:m fprintf(' \t%d\t\t%f\t%f\n', i, error_train(i), error_val(i)); end %学习曲线函数 m = size(X, 1); error_train = zeros(m, 1); error_val   = zeros(m, 1);  for i = 1:m          theta = trainLinearReg(X(1:i, :), y(1:i),lambda);       error_train(i) = linearRegCostFunction(X(1:i, :), y(1:i),theta,0);       error_val(i) = linearRegCostFunction(Xval, yval,theta,0);      end end 

5.多项式回归的特征建立

p = 8; X_poly = polyFeatures(X, p); [X_poly, mu, sigma] = featureNormalize(X_poly); X_poly = [ones(m, 1), X_poly]; X_poly_test = polyFeatures(Xtest, p); X_poly_test = bsxfun(@minus, X_poly_test, mu); X_poly_test = bsxfun(@rdivide, X_poly_test, sigma); X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test]; X_poly_val = polyFeatures(Xval, p); X_poly_val = bsxfun(@minus, X_poly_val, mu); X_poly_val = bsxfun(@rdivide, X_poly_val, sigma); X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val]; %polyFeatures函数 X_poly = zeros(numel(X), p); for i = 1 : p     X_poly(:,i) = X.^i; end end %featureNormalize函数 mu = mean(X); X_norm = bsxfun(@minus, X, mu); sigma = std(X_norm); X_norm = bsxfun(@rdivide, X_norm, sigma); end 

6.多项式回归的学习曲线

lambda = 0; [theta] = trainLinearReg(X_poly, y, lambda); figure(1); plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5); plotFit(min(X), max(X), mu, sigma, theta, p); xlabel('Change in water level (x)'); ylabel('Water flowing out of the dam (y)'); title (sprintf('Polynomial Regression Fit (lambda = %f)', lambda)); figure(2); [error_train, error_val] = ... learningCurve(X_poly, y, X_poly_val, yval, lambda); plot(1:m, error_train, 1:m, error_val); title(sprintf('Polynomial Regression Learning Curve (lambda = %f)', lambda)); xlabel('Number of training examples') ylabel('Error') axis([0 13 0 100]) legend('Train', 'Cross Validation') %plotFit hold on; x = (min_x - 15: 0.05 : max_x + 25)'; X_poly = polyFeatures(x, p); X_poly = bsxfun(@minus, X_poly, mu); X_poly = bsxfun(@rdivide, X_poly, sigma); X_poly = [ones(size(x, 1), 1) X_poly]; plot(x, X_poly * theta, '--', 'LineWidth', 2) hold off end 

7.选择λ交叉验证

[lambda_vec, error_train, error_val] = ... validationCurve(X_poly, y, X_poly_val, yval); close all; plot(lambda_vec, error_train, lambda_vec, error_val); legend('Train', 'Cross Validation'); xlabel('lambda'); ylabel('Error'); fprintf('lambda\t\tTrain Error\tValidation Error\n'); for i = 1:length(lambda_vec) fprintf(' %f\t%f\t%f\n', ... lambda_vec(i), error_train(i), error_val(i)); end