二分?三分!
闲来无事,复习一下二分/三分,我们知道,二分其实就是查找,当然有人说二分答案,二分答案不也是查找吗?在一个有序序列中查找某个元素是否存在,这就是二分的精髓所在,那么我们来复习一下原理:
假设存在一个有序(非增/非减)序列,我们要查找一个数是否存在于该序列,就可以使用二分法了,举个栗子:
上图中left和right分别是区间的左右端点,middle是区间的中部,他们存在一个关系:middle = (left+right)/2,这里的除法是按照高级语言中的整型变量相除向下取整的规则,如上图第三步,left = 8,right = 9,middle = 17/2 = 8,二分法使用的原理是分而治之,逐步减小搜索范围,每次可以减少当前区间一半的搜索范围,因此查找的时间复杂度是log n,这个例子查找23,朴素查找就是从头一个一个找,需要8次,而二分三次就可以找到了,算法优秀程度可见一斑
为什么可以通过middle指向的元素值缩小一半的搜索范围呢?
因为是有序序列啊!例子上举的是非减序列,当middle指向的值都小于期待查找的数时,middle左边的值是否一定没有查找的意义?答案是肯定的,于是我们只要调整区间左端点就可以重新计算middle在右半区间查找了,整个左半区间就可以舍去了
这里给一个整数二分的模板:
bool Binary_Search(int le,int ri,int exp,int num[])
{
while(le <= ri)
{
int mid = (le+ri)>>1;
if(num[mid] == exp) return true; //中间值与期望值相等;
else if(num[mid] > exp) ri = mid-1; //调整右区间;
else le = mid+1; //调整左区间;
}
return false; //没有找到期望值;
}
为什么要强调整数二分?因为整数可以看做是离散的区间,每两个整数都不是连续的,所以改变区间的时候le = mid+1或ri = mid-1都是以1为单位,而小数是连续不断的,在二分的时候写法和整数不一样,具体写法取决于精度要求,这里写一个:
double Binary_Search(double le,double ri,int exp)
{
while(ri-le > 0.001) //精度是保留两位小数,相差0.001不到就认为两数相等了;
{
int cnt = 0;
double mid = (le+ri)/2;
while(Condition0) //某个条件;
{
if(Condition1) cnt++; //满足一些条件;
}
if(cnt < exp) ri = mid; //修改右区间;
else le = mid; //修改左区间;
}
return le; //根据需要返回左/右区间;
}
值得注意的是,小数二分往往不是查找某个值,因为上下界已知的话,某个值是否存在区间内已经一目了然(小数连续!),小数二分往往是为了得到某个最优解(最大值、最小值问题),因此我们比较的值往往是某个受条件控制的变量,如上面的cnt,而不是直接比较区间左右端点元素值,模板没法说清一些情况,下面我们通过一些例题说明:
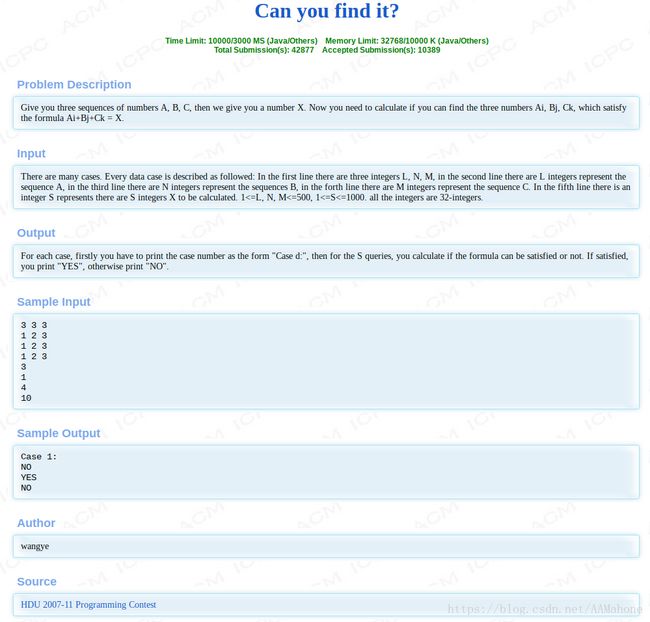
例题1:Can you find it?
题目大意: 第一行输入三个数,代表序列A,B,C的长度
第二~四行输入 三个序列,分别是A,B,C
第三行输入一个数n,代表接下来n组测试数据
接下来的n行,输入一个数X,询问是否能在序列A,B,C中分别找一个数a,b,c,使得a+b+c = X
先输出样例编号,如Case ?:
接下来的每一行,对每个询问:存在输出YES,不存在输出NO
我们分析一下常规做法,瞎暴力!对于每个区间,最坏的结果是都遍历一遍,这样按照最长的区间长度考虑需要500^3次,对于一组数据,一次询问需要这么多,一共n次询问,最坏的结果是,1000*500^3,这只是一组样例,大概计算1.25e11次,我们有3s的时间(C++),估算最多能够执行3e8次(可能更少),妥妥的超时!何况我们还有多组样例,因此考虑二分,在二分之前,我们先预处理一下:如果我们把两个序列中所有元素两两相加的所有结果都保存下来(最多有500*500中结果)合成一个新序列,再使用这个新序列和剩下的一个序列两两相加查找是否满足约束条件(当然需要二分优化),这样就不会超时了,注意一下输入输出格式,具体的二分优化可以看我的代码:
#include
#include
#include
using namespace std;
int l,n,m;
vectora;
vectorb;
vectorc;
vectormg;
bool check(int ans)
{
for(int i = 0; i < c.size(); i++)
{
if(binary_search(mg.begin(),mg.end(),ans-c[i])) //对合并后的序列进行二分搜索;
return 1;
}
return 0;
}
int main()
{
int t,cc = 0,ans;
while(cin>>l>>n>>m)
{
cc++;
a.clear();
b.clear();
c.clear();
mg.clear();
for(int i = 0; i < l; i++)
{
cin>>t;
a.push_back(t);
}
for(int i = 0; i < n; i++)
{
cin>>t;
b.push_back(t);
}
for(int i = 0; i < m; i++)
{
cin>>t;
c.push_back(t);
}
for(int i = 0; i < l; i++)
for(int j = 0; j < n; j++)
mg.push_back(a[i]+b[j]); //序列合并;
sort(mg.begin(),mg.end()); //排序以便二分;
cout<<"Case "<>t;
while(t--)
{
cin>>ans;
if(check(ans)) cout<<"YES"<
上面的代码需要讲一下,我是直接使用了C++提供的binary_search函数,这个函数是对一个区间进行二分查找的函数,返回值为bool,即找到与否,传入的参数是区间始点、终点以及期望值,如我上文的代码,传入的是合并的新序列的始末端点,期望值是X-c[i],若找到说明有X-c[i] = mg[j],即x-c[i] = a[j]+b[k],即X = a[j]+b[k]+c[i],(i,j,k为任意值)也就是符合题意的解,找到即可立刻退出,返回1 ,这里有一个小小的优化想必各位也注意到了,那就是对合并的序列二分而不是对剩余的序列二分,因为合并的序列更长,更能体现二分优秀的时间复杂度,上面使用的vector就不提了,懒癌发作不想手写二分,但是数组莫名其妙判错,只得使用万能的STL搞掉这一题,不过,STL是真的快,看看时间复杂度就知道了(题目给了3000MS,只用了不到500MS):
![]()
另:终于找到错误原因了!原来是数组长度没有把握好!放一个刚写的代码:
#include
#include
using namespace std;
int a[505],b[505],c[505],mg[250005],l,n,m;
bool check(int ans)
{
for(int i = 0; i < m; i++)
{
if(binary_search(mg,mg+l*n,ans-c[i])) //错误原因在于合并后数组长度!原来我一直写的l+n实际是l*n;
return 1;
}
return 0;
}
int main()
{
int t,cnt = 0,k,ans;
while(cin>>l>>n>>m)
{
cnt++;
k = 0;
for(int i = 0; i < l; cin>>a[i++]);
for(int i = 0; i < n; cin>>b[i++]);
for(int i = 0; i < m; cin>>c[i++]);
for(int i = 0; i < l; i++)
for(int j = 0; j < n; j++)
mg[k++] = a[i]+b[j];
sort(mg,mg+k);
cout<<"Case "<>t;
while(t--)
{
cin>>ans;
if(check(ans)) cout<<"YES"<
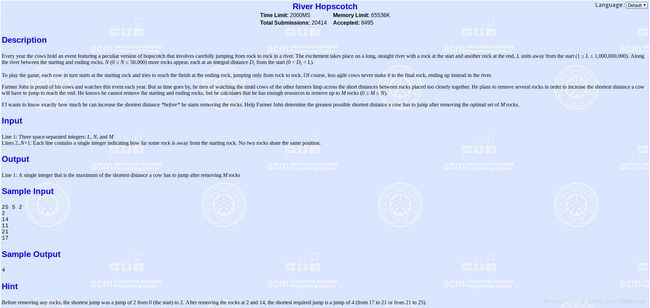
例题2:River Hopscotch
这是个二分好题!同样是个经典题,题目大意:
第一行输入三个数L,N,M,代表一条河宽度为L,有N块石头在河中,你需要移走M块石头,使得剩余陆地的距离(石头与石头、石头与河岸)之间的最小距离最大
接下来的N行,输入一个数m,代表离左侧河岸m米处有一块石头(右侧河岸显然离左侧河岸L米,左侧河岸在0米处)
要你输出:最大的最小距离
题解见代码,代码如下:
#include
#include
using namespace std;
int main()
{
int l,n,m,dis[50010],le,ri;
cin>>l>>n>>m;
dis[0] = 0,dis[n+1] = l;
for(int i = 1; i <= n; i++)
cin>>dis[i];
sort(dis,dis+n+1);
le = dis[0],ri = l; //确立初始的左右端点;
while(le <= ri) //二分;
{
int mid = (le+ri)>>1,cnt = 0,before = 0; //我们假设最大的最小距离是mid;
for(int i = 1; i <= n+1; i++) //before存的是上一次连续拿走石头的开始位置;
{
if(mid >= dis[i]-dis[before]) cnt++; //连续拿走石头;
else before = i; //连续被打断,重新记录before位置;
}
if(cnt > m) ri = mid-1; //拿走的石头数量超过m块,显然mid偏大;
else le = mid+1; //mid偏小或有解但不一定是最优解;
}
cout<
![]()
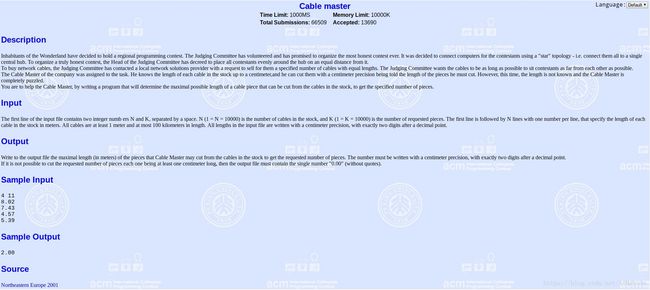
例题3:Cable master
题目大意:第一行输入N和K,表示有N根网线,需要分成等长的K段
接下来的N行,表示每根网线的长度
要你输出:在能分成K段的前提下,每段最大的长度(保留两位小数),若不存在,则输出0.00
这个题目就是一个典型的小数二分,我们只需要一开始标记左右端点,左端点(下界)显然是0,右端点(上界)是这N根网线的最大长度,可以边输入边找出,那么,分成的K段长度一定在左右端点构成的区间之间,我们只需要二分枚举这个值,用每根网线的长度除以mid值,向下取整(C++的floor()函数很好用),就可以统计这N根网线能分多少段了,如果大于K,说明太长了,需要调整左端点,否则说明太短/还有更大的解,调整右端点即可,注意最后的保留两位小数,坑人,代码如下:
#include
#include
using namespace std;
int main()
{
int n,m;
double len[10010],_max = 0;
scanf("%d%d",&n,&m);
for(int i = 0; i < n; i++)
{
scanf("%lf",&len[i]);
if(len[i] > _max) _max = len[i]; //小技巧,边输入边找最大值;
}
double le = 0,ri = _max; //左右端点;
while(ri-le > 0.001) //精度0.01,只要左右端点的差值小于0.001就认为相等;
{
int cnt = 0;
double mid = (le+ri)/2; //假设mid是当前最大分段单位;
for(int i = 0; i < n; i++)
cnt += floor(len[i]/mid); //一根网线在当前分段单位下,能分几段;
if(cnt < m) ri = mid; //分段数小于需求,说明mid过大;
else le = mid; //mid过小或不是最优解;
}
printf("%.2lf\n",floor(ri*100)/100); //保留两位小数,坑点;
return 0;
}
![]()
那么接下来我们看看三分:
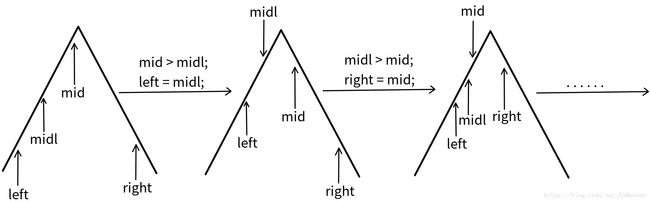
三分和二分类似,但是处理的不是有序序列的问题,处理的一般是先增后减或者先减后增的变化问题,可以抽象为一元二次函数图像类似的图,一般让你求最值(函数图像顶点取值),这样的问题我们可以三分,三分的思想是,根据左右端点,求得mid(这一步和二分如出一辙),然后根据mid和其中一个端点(比如左端点)求出midl(midl = (l+mid)/2),最后比较midl和mid处的函数值来调整左右端点,调整原理如下图:
上图中的曲线为先增后减,作为F(x),取mid和midl,由mid = (left+right)/2,midl = (left+mid)/2可知,midl位置上永远在mid左边,若F(midl) < F(mid),说明mid比midl更靠近极值,我们舍去左区间,调整左端点-> left = midl,而后F(midl) > F(mid)说明midl更靠近极值,我们应该舍去右区间,调整右端点-> right = mid,如此反复应用上面两条规则,最终能让right-left无限趋近于0,则可以认为F(left)或F(right)是答案了,写一个模板:
void Triple_Search(double l,double r)
{
while(r-l >= 1e-9) //认为左右端点相等;
{
double mid = (l+r)/2;
double midl = (mid+l)/2;
double d1 = cal(mid); //cal可以代表函数表达式,计算当前点的函数值;
double d2 = cal(midl);
if(d1 >= d2) l = midl; //左端点更新;
else r = mid; //右端点更新;
}
printf("%.3lf\n",cal(l)); //近似的极值;
}
以上模板是根据函数先增后减写的,先减后增的函数请自行琢磨,PS:三分不存在什么整数区间三分,因为函数是连续的,定义在连续区间上,而整数是离散的,前面说过了,所以三分都是double型的
来一个三分的题目吧: Light Bulb
题目大意已经很明了了:第一行输入一个T表示测试数据组数
接下来的每一行输入三个数,表示H,h和D,代表如图所示的数据
对于每组样例,输出一行,表示人在灯光下影子的最大长度,保留三位小数
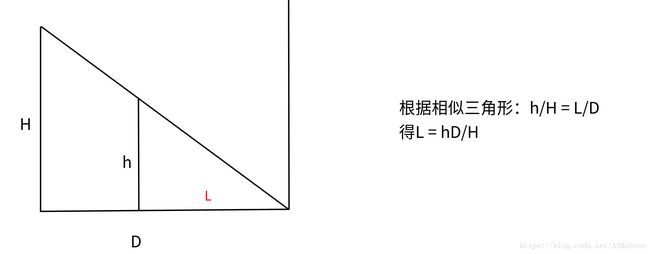
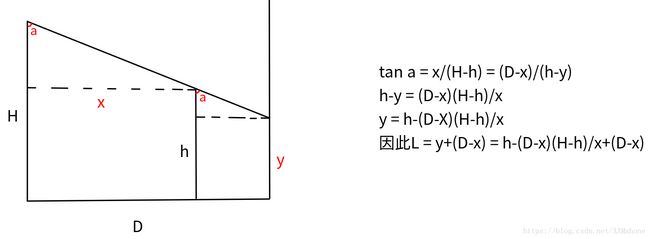
这题可以这么分析,显然,从人正好在灯下时,到人的影子刚好延伸到墙角时,这一段影长是单调递增的,可以不考虑,当人的影子上墙后,是先增后减的趋势,这个容易推导,当影子正好延伸到墙角时长度一定比人靠墙时更长,而人在这个过程中影子有一个先变长再变短的阶段。设人到灯下的距离为x,影长为L(x),x取值范围显然是[0,D],所以我们三分函数L(x)的起点可以不从x = 0开始,而是从某个x,使得L(x)+x = D开始(影子刚好延伸到墙上),如此便将前面递增的一段区间删去,直接从后面的先增后减区间开始求,至于为什么要删去,显然影子之前递增的函数和之后先增后减的函数不是同一个(这就是说,L(x)是一个分段函数),为了简化计算去掉前面一段(前面一段的最值已经找到,并没有计算的必要),我们在后面一段找最值即可,这里画一个推导的图解(两种特殊情况):
根据上图我们可知,三分开始的左端点是D-hD/H,右端点是D,三分函数是:L(x) = h-(D-x)(H-h)/x+(D-x),代码就很套路了:
#include
#include
using namespace std;
double H,h,D;
double cal(double x)
{
return h-(H-h)*(D-x)/x+D-x; //计算影子长度的推导公式;
}
int main()
{
int T;
double x,l,r;
cin>>T;
while(T--)
{
cin>>H>>h>>D;
l = D-h*D/H,r = D; //确定初始区间;
while(r-l >= 1e-9)
{
double mid = (l+r)/2; //二分;
double midr = (mid+r)/2; //三分;
double d1 = cal(mid);
double d2 = cal(midr);
if(d1 >= d2) r = midr; //舍去右区间;
else l = mid; //舍去左区间;
}
printf("%.3lf\n",cal(l)); //近似答案;
}
return 0;
}
![]()
总结一下,
二分系列:如果是二分查找的题目,问你是否存在的问题,一般直接使用Algorithm里的binary_search()就可以了,具体的还可以配合lower_bound()以及upper_bound()食用更佳!如果是二分答案的题目(即二分出来的值就是答案),需要自己手写二分,并且注意题目输出,如果不确定二分结束后该输出左端点还是右端点,可以冒着WA的风险交几发,一般都是输出左/右端点,还要注意小数二分的精度问题哦~
三分系列:三分难点在于找函数,找三分起始左右区间,以及小数判等的处理和精度问题等,还有函数的图像必须只能有一个转折点(上凸或下凹),最后是区间的取舍问题,总之记住:谁离最值远,舍去谁在的区间~
PS:二分三分只是个思想,题型不可能全部讲到,重要的还是,刷题,掌握技巧和方法