C#内功修炼(算法)——树(二 )
树结构
树是一种重要的非线性数据结构,直观地看,它是数据元素(在树中称为结点)按分支关系组织起来的结构,很象自然界中的树那样。
树是一种重要的非线性数据结构,直观地看,它是数据元素(在树中称为结点)按分支关系组织起来的结构,很象自然界中的树那样。树结构在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用,如在编译源程序如下时,可用树表示源源程序如下的语法结构。又如在数据库系统中,树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。
树的关系复杂使用链式存储
1,双亲表示法
![]()
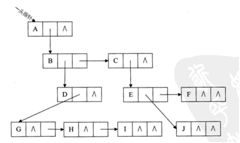
2,孩子表示法
![]()
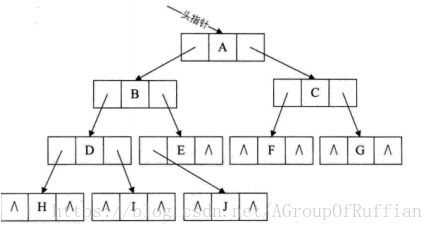
3,孩子兄弟表示法
![]()
二叉树:
一般的树来说是一对多的关系,使用顺序结构存储起来比较困难,但是二叉树是一种特殊的树,每个结点最多有两个子节点,并且子节点有左右之分,并且兄弟,父亲,孩子可以很方便的通过编号得到,所以我们使用顺序存储结构使用二叉树的存储。
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域,我们称这样的链表为二叉链表。
![]()
二叉树特性:
1,在二叉树的第i层上最多有 2i-1个结点(i>=1)
2,深度为k的二叉树至多有2k-1个结点
20+21+22+23+24+25+26+27+.....+2k-1+-1
=1+20+21+22+23+24+25+26+27+.....+2k-1-1
=21+21+22+23+24+25+26+27+.....+2k-1-1
=22+22+23+24+25+26+27+.....+2k-1-1
=23+23+24+25+26+27+.....+2k-1-1
=2k-1+2k-1-1
=2k-1
3,对于一个完全二叉树,假设它有n个结点,对结点进行从1开始编号,对任一结点i满足下面
a,它的双亲是结点i/2 (除了i=1的情况)
b,左孩子是2i 右孩子是2i+1
c,如果2i>n 说明无左孩子 2i+1>n说明无右孩子
二叉树储存:
顺序储存:
private char[] _data = new[] {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J'};
private void UseTree()
{
BiTree biTree = new BiTree(_data.Length);
for (int i = 0; i < _data.Length; i++)
{
biTree.Add(_data[i]);
}
}
public class BiTree
{
public T[] Data;
public int Count;
public BiTree(int capactiy)
{
Data = new T[capactiy];
Count = 0;
}
public bool Add(T item)
{
if (Count >= Data.Length) return false;
Data[Count] = item;
Count++;
return true;
}
} 链式储存:
二叉树遍历:
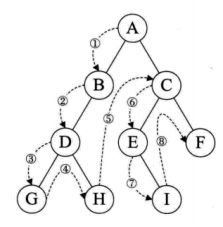
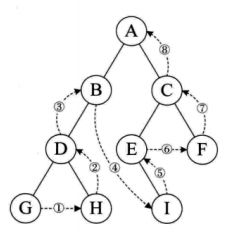
1,前序遍历
先输出当前结点的数据,再依次遍历输出左结点和右结点
///
/// 前序遍历
///
public void FirstTraversal(int index)
{
if (index >= Data.Length) return;
//遍历节点编号
int munber = index + 1;
if (Data[index].Equals(-1)) return;
Debug.Log(Data[index]);
int leftNumber = munber*2;
int rightNumber = munber*2 + 1;
FirstTraversal(leftNumber - 1);
FirstTraversal(rightNumber - 1);
}
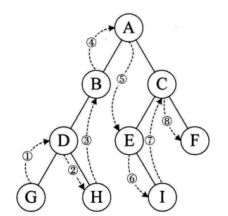
2,中序遍历
先遍历输出左结点,再输出当前结点的数据,再遍历输出右结点
GDH B A E I C F
///
/// 中序遍历
///
public void MiddleTraversal(int index)
{
if (index >= Data.Length) return;
//遍历节点编号
int munber = index + 1;
if (Data[index].Equals(-1)) return;
int leftNumber = munber * 2;
int rightNumber = munber * 2 + 1;
MiddleTraversal(leftNumber - 1);
Debug.Log(Data[index]);
MiddleTraversal(rightNumber - 1);
}
3,后序遍历
先遍历输出左结点,再遍历输出右结点,最后输出当前结点的数据
G H D B I E F C A
///
/// 后序遍历
///
public void LastTraversal(int index)
{
if (index >= Data.Length) return;
//遍历节点编号
int munber = index + 1;
if (Data[index].Equals(-1)) return;
int leftNumber = munber * 2;
int rightNumber = munber * 2 + 1;
LastTraversal(leftNumber - 1);
LastTraversal(rightNumber - 1);
Debug.Log(Data[index]);
}
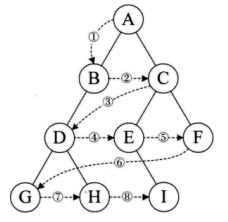
4,层序遍历
从树的第一层开始,从上到下逐层遍历,在同一层中,从左到右对结点 逐个访问输出
///
/// 层遍历
///
public void LayerTraversal()
{
for (int i = 0; i < Count; i++)
{
Debug.Log(Data[i]);
}
}二叉排序树:
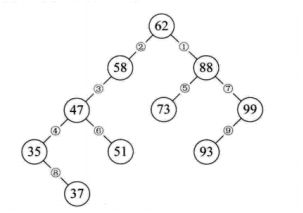
二叉排序树,又称为二叉查找树。它或者是一棵空树,或者是具有下列性质的二叉树。
若它的左子树不为空,则左子树上所有的结点的值均小于根结构的值;
若它的右子树不为空,则右字数上所有结点的值均大于它的根结点的值;
它的左右子树也分别为二叉排序树。
///
/// 树类
///
public class BSTree
{
private BSNode _rootNode;
///
/// 增加
///
///
public void Add(int item)
{
BSNode newNode = new BSNode(item);
if (_rootNode == null)
{
_rootNode = newNode;
}
else
{
BSNode temp = _rootNode;
while (true)
{
if (item >= temp.Data) //放右面
{
if (temp.RightNode == null) //右节点空
{
temp.RightNode = newNode;
temp.ParentNode = temp;
break;
}
temp = temp.RightNode;
}
else //放左面
{
if (temp.LeftNode == null)
{
temp.LeftNode = newNode;
temp.ParentNode = temp;
break;
}
temp = temp.LeftNode;
}
}
}
}
///
/// 查找
///
public bool Find(int item, BSNode node)
{
if (node == null) return false;
if (node.Data == item) return true;
if (item > node.Data) return Find(item, node.RightNode);
if (item < node.Data) return Find(item, node.LeftNode);
return false;
}
///
/// 删除
///
public bool Delete(int item)
{
BSNode temp = _rootNode;
while (true)
{
if (temp == null) return false;
if (temp.Data == item)
{
Delete(temp);
return true;
}
temp = temp.Data > item ? temp.LeftNode : temp.RightNode;
}
}
private void Delete(BSNode node)
{
if (node.ParentNode == null)
{
_rootNode = null;
return;
}
//判断是否是叶节点
if (node.LeftNode == null && node.RightNode == null)
{
if (node.ParentNode.LeftNode == node)
node.ParentNode.LeftNode = null;
else
node.ParentNode.RightNode = null;
return;;
}
//只有左子树或只有右子树
if (node.LeftNode == null && node.RightNode != null)
{
node.Data = node.RightNode.Data;
node.RightNode = null;
return;
}
if (node.LeftNode != null && node.RightNode == null)
{
node.Data = node.LeftNode.Data;
node.LeftNode = null;
return;
}
//左右子树都有
BSNode temp = node.RightNode;
while (true)
{
if (temp.LeftNode != null)
{
temp = temp.LeftNode;
}
else
{
break;
}
}
node.Data = temp.Data;
Delete(temp);
}
}
///
/// 节点类
///
public class BSNode
{
public int Data { get; set; }
public BSNode LeftNode { get; set; }
public BSNode RightNode { get; set; }
public BSNode ParentNode { get; set; }
public BSNode(int item)
{
Data = item;
LeftNode = null;
RightNode = null;
ParentNode = null;
}
}