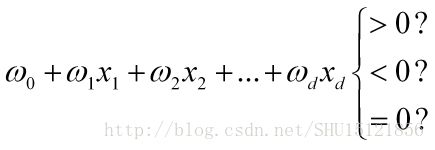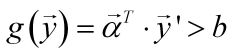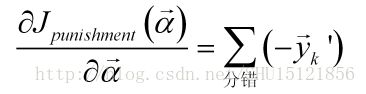【ML学习笔记】18:原始的Perceptron(感知机)
感知机的决策面
感知机用来获取样本特征空间中的一个超平面,以对样本进行分类,属于线性分类器。
这样的分类问题比较经典,如某一个参加非诚入扰的女士(分类器)评判自己会不会给非诚勿扰的各个男嘉宾(样本)留灯(1或者-1),男嘉宾作为样本,有多个特征,如身高、月收入、长相得分等。
女嘉宾的内心对这些特征会有一个权重,她想的是:把这些特征乘以权重(当然对某些特征的权重是负的,比如每周抽烟的数目)加起来,得到总得分:
![]()
如果得分超过某个数字,那么就留灯(判为1);如果得分小于这个数字,那么就灭灯(判为-1);如果得分恰好等于这个数字,那么女嘉宾十分纠结(拒判):
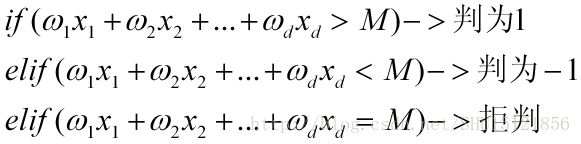
取x0=1,则判别函数可以表示成两个向量的内积:
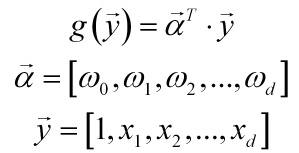
这两个列向量都添加过第0号项,分别称为增广权重向量和增广样本特征向量。
在特征空间中,权重向量内积样本向量则是用过原点的超平面作判决,两个向量增广以后,因为加了常数项,所以是用任意位置的超平面作判决:
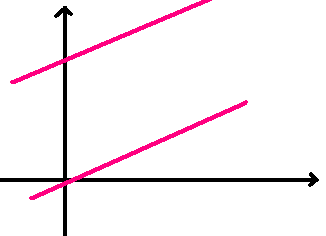
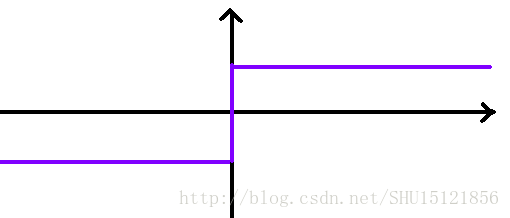
对于投入的样本特征向量y,用感知机算出一个数,如果大于0就判为1,小于0就判为-1,在0处是跳变的(不同于sigmoid函数):
感知机的训练
感知机的训练目标就是得到增广的权向量,对于训练集中的每个样本,需要判定它是否符合当前增广权重向量的分类,如果不符合,就需要对增广权重向量进行调整,直到训练集中所有的样本都被增广权重向量表示的可以处在任意位置的超平面正确分类。
这是最原始的感知机,因为是”直到”,所以要求样本是线性可分的,也就是对于所有的样本,能够找到这样的增广权向量,使所有样本都被正确分类。
为了方便”判定它是否符合当前增广权重向量的分类”,可以让本来需要判别函数<0的那些样本增广样本向量取反,取反也就是乘以-1,这样只需要判定:
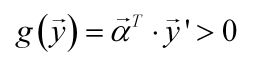
是否成立即可。这样定义的y’是规范化增广样本特征向量。
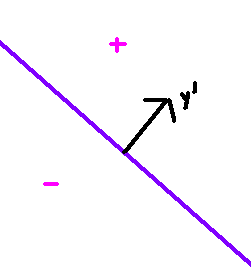
对于每一个样本y’,满足上式的增广权重向量只需要和它的夹角<90度,就可以满足内积>0,这样所有的符合条件的增广权重向量完全等同于垂直于样本y’向量的超平面正侧的所有向量,因为这些向量都能满足和它内积>0:
对于训练集中的所有样本,每个样本都能找到这样的超平面,它们的正侧的交集即成为一个比较窄的区域,称为解区:
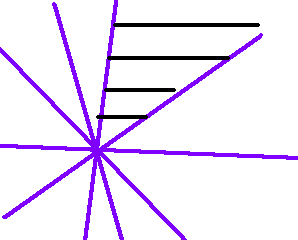
在解区内的向量即是训练算法要寻找的解向量,都是能把所有训练集样本正确分类的增广的权向量。
当然,靠近解区边缘的向量可能不太具好的泛化能力,可以使用余量 b来让手动让解区更狭窄,从而找到落在原来解区中央的解向量:
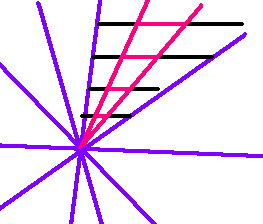
要寻找解区里的解向量作为增广权重向量,可以先设定一个向量。
显然这个值越小,错误的程度也就越强。因此感知机准则函数可以取负加和:
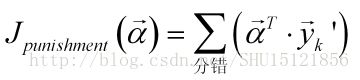
作为用当前这个增广权重向量作判别的损失。
所以目标就是求使得这个损失最小(在线性可分的情况下必须是0)的增广权重向量:
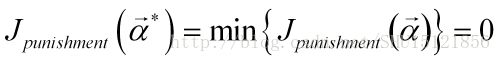
梯度下降法求损失函数最小的解向量
从任给定的一个增广权重向量开始,沿着损失函数梯度方向的反方向,按照一个步长来求极小值(如果它就是最小值):
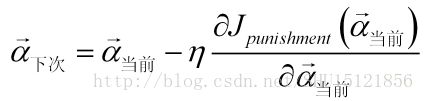
这里的步长yita也称学习率,如果学习率太大,会导致不停的波动,总是没法落入解区;如果学习率太小,那么可能需要较多的迭代次数。
在这次的代码里,没有改变学习率,实际上学习率应该随着迭代的推进变小,这样才能较快接近解区然后较缓慢地进入解区。
所以迭代公式变为:
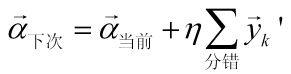
相当于把分错的样本增广特征向量以学习率为系数加到增广权重向量上。
注意
①在实际使用时,如果把每次迭代的所有错分样本加起来一起修正增广权重向量,效率不高。应该在迭代中每次发现错分样本即刻修正增广权重向量。
②样本不是线性可分时,可以让学习率在梯度下降过程中逐步减少,强制收敛,获得一个可用的解。
代码实现
#-*-coding:utf-8-*-
from numpy import *
import operator
from matplotlib import pyplot as plt
#获取数据
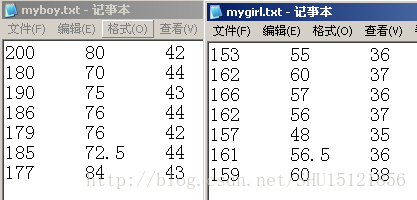
def getData():
fr1=open(r'myboy.txt')
fr0=open(r'mygirl.txt')
arrayOLines1=fr1.readlines() #读取文件
arrayOLines0=fr0.readlines()
#特征矩阵
dataMat1=[]
dataMat0=[]
#男同学
for line in arrayOLines1:
line=line.strip() #strip()去掉首尾空格
listFromLine=line.split() #按空白字符分割成列表
#string变float
for i in range(len(listFromLine)):
listFromLine[i]=float(listFromLine[i])
#加入特征矩阵
dataMat1.append(listFromLine)
#女同学
for line in arrayOLines0:
line=line.strip() #strip()去掉首尾空格
listFromLine=line.split() #按空白字符分割成列表
#string变float
for i in range(len(listFromLine)):
listFromLine[i]=float(listFromLine[i])
#加入特征矩阵
dataMat0.append(listFromLine)
return dataMat1,dataMat0
#传入迭代次数和训练集,梯度上升训练感知机
def TraPCPT(xMat,yLab):
omg=mat([1,1,1]) #初始w0(偏置),w1=,w2
n=0 #统计循环次数
yita=0.05 #学习率
lnth=len(xMat) #总的样本数
xMat=mat(xMat) #二维列表矩阵化
yLab=mat(yLab) #一维列表向量化
#梯度上升直到进入解区
while(True):
n+=1
ok=True #用ok来判定收敛是否结束
#smy=mat([0.0,0.0,0.0]) #把错分的规范化样本yi加起来
#N-=1
#每次求得真的realyLab=f(x)的列向量
realyLab=xMat*omg.T
#对每个样本求出来的f(x)值
for i in range(lnth):
#若点此时的分类位置不对
if yLab[0,i]*realyLab[i,0]<=0:
ok=False
'''
#规范化后加到smy向量里
smy=smy+yLab[0,i]*xMat[i]
'''
#在学习率yita下修正权值向量
omg=omg+yita*yLab[0,i]*xMat[i]
if ok==True: #如果已经收敛
break
print '循环了',n,'次'
return omg #返回权值向量
#演示
def Go(i,j):
dataMat1,dataMat0=getData()
#i,j号特征在男女类各自的列表
Ftr1i=[line[i] for line in dataMat1]
Ftr1j=[line[j] for line in dataMat1]
Ftr0i=[line[i] for line in dataMat0]
Ftr0j=[line[j] for line in dataMat0]
#绘制男女离散的点
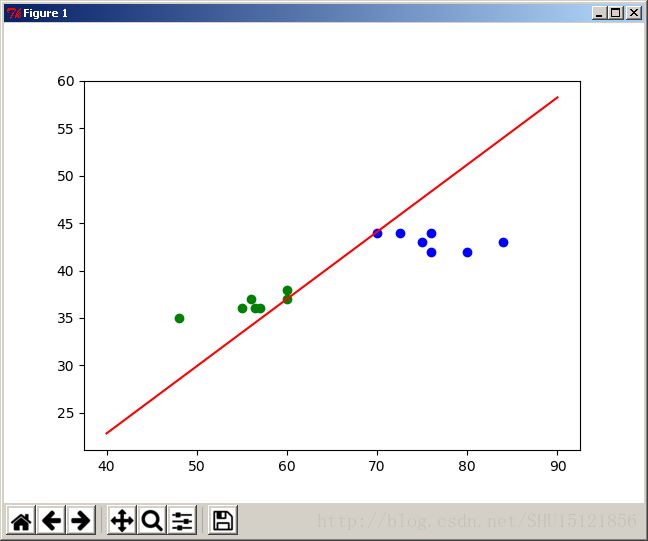
plt.scatter(Ftr1i,Ftr1j,c=u'b',label='male')
plt.scatter(Ftr0i,Ftr0j,c=u'g',label='female')
#xMat每行存[x0=1,x1=i特征值,x2=j特征值]
#yLab[k]存xMat中第k行对应的1(男),或-1(女)
'''
xMat=[]
yLab=[]
#交叉放入的方式(扔掉了不一样多的那块数据)
lnth=min(len(Ftr1i),len(Ftr0i)) #取比较小的
for k in range(lnth):
xMat.append([1,Ftr1i[k],Ftr1j[k]])
yLab.append(1)
xMat.append([1,Ftr0i[k],Ftr0j[k]])
yLab.append(-1)
'''
#先放男的
xMat=[[1,Ftr1i[k],Ftr1j[k]] for k in range(len(Ftr1i))]
yLab=[1 for k in range(len(Ftr1i))]
#再临时放女的
xMat0=[[1,Ftr0i[k],Ftr0j[k]] for k in range(len(Ftr0i))]
yLab0=[-1 for k in range(len(Ftr0i))]
#把女的扩展进来
xMat.extend(xMat0)
yLab.extend(yLab0)
'''
xMat=[[1,Ftr0i[k],Ftr0j[k]] for k in range(len(Ftr0i))]
yLab=[-1 for k in range(len(Ftr0i))]
xMat1=[[1,Ftr1i[k],Ftr1j[k]] for k in range(len(Ftr1i))]
yLab1=[1 for k in range(len(Ftr1i))]
xMat.extend(xMat1)
yLab.extend(yLab1)
'''
#训练以获得参数
omg=TraPCPT(xMat,yLab)
#omg=mat([-500,3,8])
print 'new omg',omg
#绘制曲线用的横坐标(i特征)
if i==0:
lft=140
rgt=210
elif i==1:
lft=40
rgt=90
else:
lft=30
rgt=47
x1=linspace(lft,rgt,10) #反正是直线,不用采样太多
#绘制得到的直线
o1=float(omg[0,1])
o0=float(omg[0,0])
o2=float(omg[0,2])
plt.plot(x1,-(o1*x1+o0)/o2,c=u'r')
plt.show() #显示