python实现单层感知机(perceptron)

前言

最近在学习李航教授著作《统计学习方法》，刚刚起步单纯学概念也是有点无聊，于是乎就想利用python复现一下感知机。因为不是大佬，一是机器学习方面的水准不算很高，二来python不是本人熟悉的语言，语法难免僵硬，抑或说是java化，各种不足也敬请谅解。

简单介绍

原理

相信各位愿意继续阅读我的文章的，基本不是想了解感知机原理的，原理介绍网上一大堆，我也不浪费篇幅来写了，感觉大家可以一边看我的代码实现，一边看一下其他介绍原理的文章，这样会比较好理解。
本人是通过《统计学习方法》一书进行的学习的，原理结合了书本和网上的一些资料。这里我只简单介绍一下感知机。

感知机（perceptron）是一种二分类的线性分类模型，最最简单的感知机只能做到线性的二分类，当然经过研究现在多层感知机（维基解释）已经可以做到非线性分类了。不过感知机仍是很多机器学习算法的基础。

权值更新

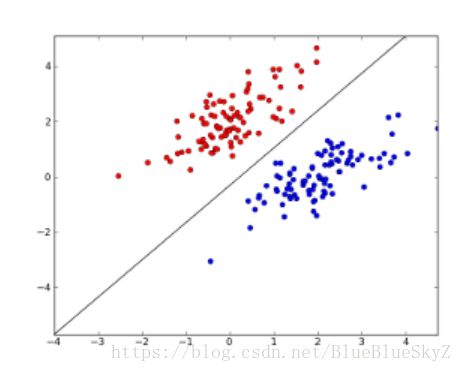
我们的目标是找到一条直线，使其能完成二分类，这条直线的参数就是我们想要找到的。直线的表达形式有两种x(2) = k*x(1) + b和a*x(1) + b*x(2) + c = 0，这两个我等会都会用到，第一个使用比较方便，我会使用其作为初始点的生成，第二种是因为书本上是使用这个做的权值更新（偷个懒）。

感知机学习是误分类驱动的，利用了随机梯度下降法（stochastic gradient descent）。找到一个误分类点，然后根据下面的公式改变权值，这样可以使误分类点的数量变少。

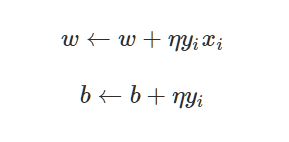
其中，x为输入的坐标，包含点的x轴、y轴坐标，书上称之为x(1)、x(2)轴；

y为分类结果，如果输入的点在直线的上下为1或-1，当然这个上下我觉得不是简单的视觉上的上下，这里只是我想说的严谨一点，代码写还是那么写；

η为学习率了你直线的适应速度，学习地快是好事，但是学习快就不踏实，即最终的分类结果可能不是完美的；学习率低相对来说学得就慢，如果给足时间，可以精确分类。所以我们可以在前期给大学习率，后期给小学习率，就像先抓重点，再抓细节。不过这一点我还没实现，先留个小小的遗憾吧，之后有空再补了。

这里还是建议大家有机会好好消化书本或者网上的博文，实现的难点和关键在此。

代码实现

训练点和测试点生成

基于直线生成随机分布点

我们需要一些点，这些点当然不能随机分布啦，肯定是要有一定规律的。我在一条直线附近，利用了np.random.normal产生高斯白噪声，然后生成分布点。这里我使用y=k*x+b的形式。
然后根据点的分布，给点打上标签1或-1。

'''
利用高斯白噪声生成基于某个直线附近的若干个点
y = wb + b
weight 直线权值
bias 直线偏置
size 点的个数
'''
def random_point_nearby_line(weight , bias , size = 10):
    x_point = np.linspace(-1, 1, size)[:,np.newaxis]
    noise = np.random.normal(0, 0.5, x_point.shape)
    y_point = weight * x_point + bias + noise
    input_arr = np.hstack((x_point, y_point))
    return input_arr

# 直线的真正参数
real_weight = 1
real_bias = 3
size = 100

# 输入数据和标签
# 生成输入的数据
input_point = random_point_nearby_line(real_weight, real_bias, size)
# 给数据打标签，在直线之上还是直线之下，above=1,below=-1
label = np.sign(input_point[:,1] - (input_point[:,0] * real_weight + real_bias)).reshape((size, 1))

训练集和测试集

这里使用了sklearn一个函数自动实现了分割，只要确定比例即可：

testSize = 15
x_train, x_test, y_train, y_test = model_selection.train_test_split(input_point, label, test_size=testSize)
trainSize = size - testSize

绘制初始点和直线

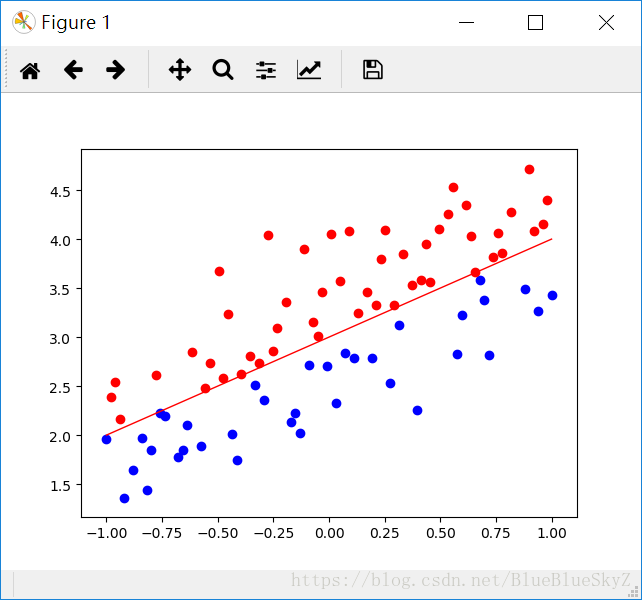
这里使用的是matplotlib中的pyplot，初始点标签为1的标红，初始点标签为-1的标蓝。然后根据一开始的直线，画出预计的效果。

# 将输入点绘图
fig = plt.figure() # 生成一个图片框
ax = fig.add_subplot(1,1,1) # 编号
for i in range(y_train.size):
    if y_train[i] == 1:
        ax.scatter(x_train[i,0], x_train[i,1], color='r') # 输入真实值(点的形式) 红色在线上方
    else:
        ax.scatter(x_train[i, 0], x_train[i, 1], color='b')  # 输入真实值(点的形式) 蓝色在线下方
plt.ion() # 互动模式开启show后不暂停
plt.show()
# initial line
lines = ax.plot([-1 , 1], [-real_weight+real_bias, real_weight+real_bias], 'r-', lw=1)
plt.pause(1.5)

训练部分实现

实现效果如图，不断参数不断修改，完成收敛：

随机梯度下降法

随机梯度下降法的过程已经在上面说了。
我们这边的生成的权重Weight的shape是(2,1)，因为坐标轴有两个，这是根据ax+bx+c=0的形式得出的。Bias的取值会比较随意了，一般会给0。

# 初始化w、b
Weight = np.random.rand(2,1) # 随机生成-1到1一个数据
Bias = 0 # 初始化为0

然后就是随机梯度下降法的实现了，这里我使用了全局变量这样就不用返回了。接下来根据输入点和目前的Weigh和Bias,生成prediction为预计的标签。预计标签与真实标签的积小于等于0则误分类，利用梯度进行下降。
这里的学习率我还是使用了过一定的轮数除以2的方式动态变化了，这样效果也不错，收敛速度较之前的固定值大大加快。

def trainByStochasticGradientDescent(input, output, input_num, train_num = 10000, learning_rate = 1):
    global Weight, Bias
    x = input
    y = output
    for rounds in range(train_num):
        for i in range(input_num):
            x1, x2 = x[i]
            prediction = np.sign(Weight[0] * x1 + Weight[1] * x2 + Bias)
            # print("prediction", prediction)
            if y[i] * prediction <= 0: # 判断误分类点
                # Weight = Weight + np.reshape(learning_rate * y[i] * x[i], (2,1))
                Weight[0] = Weight[0] + learning_rate * y[i] * x1
                Weight[1] = Weight[1] + learning_rate * y[i] * x2
                Bias = Bias + learning_rate * y[i]
                # print(Weight, Bias)
                draw_line(Weight, Bias)
                break
        if rounds % 200 == 0:
            learning_rate *= 0.5
            if compute_accuracy(input, output, input_num, Weight, Bias) == 1:
                print("rounds:", rounds)
                break;

动态绘制

接下来就是一些小部件了，为了使展示更直观，我开启了pyplot的交互模式，然后动态显示目前的直线。

def draw_line(Weight, Bias):
    global ax, lines
    x1, y1 = -1, ((-Bias-Weight[0]*(-1) ) / Weight[1])[0]
    x2, y2 = 1, ((-Bias-Weight[0]*(1) ) / Weight[1])[0]
    try:
        ax.lines.remove(lines[0])  # 抹除
    except Exception:
        # plt.pause(0.1)
        pass
    lines = ax.plot([x1, x2], [y1, y2], 'r-', lw=5)  # 线的形式
    # lines = ax.plot([-1, 1], [2, 4 + 5*np.random.rand(1)], 'r-', lw=5)  # 线的形式
    plt.show()
    plt.pause(0.01)

精确度计算

然后就是根据测试集计算精确度了，在训练的过程中我也使用了这个方法当训练集完成训练完成之后就不用循环了，减少了运行时间。
最终经过一定轮数的运算，准确率几乎是百分之百。

def compute_accuracy(x_test, y_test, test_size, weight, bias):
    x1, x2 =  np.reshape(x_test[:,0], (test_size, 1)), np.reshape(x_test[:,1], (test_size, 1))
    prediction = np.sign(y_test * ( x1 * weight[0] + x2 * weight[1] + bias ))
    count = 0
    # print("prediction",prediction)
    for i in range(prediction.size):
        if prediction[i] > 0:
            count = count + 1
    return (count+0.0)/test_size

结尾

github地址奉上，我使用的环境是py3.6，复现的整个过程还是比较揪心的，一开始用了tf，但是传入的参数始终搞不定，最终还是手撸了一遍。不过学习的过程还是有趣的，毕竟机器现在都在学习，人不能停止学习啊。

---

参考：

1. https://www.cnblogs.com/bsdr/p/5405082.html
2. 李航 《统计学习方法》