（NLP）基于分词标签的中文短文本相似度

基于分词标签的中文短文本相似度

最近接触到了一些关于中文短文本相似度的算法，将它们总结在此：

• 中文编辑距离
• 基于词频的余弦相似度
• Python difflib

github传送门：https://github.com/gongpx20069/DIYNLP

---

1.0 在相似度算法之前的分词处理

在比较两个字符串str1和str2之前，我们需要对它们进行分词处理，分词后变成两组标签（我认为分词后的标签具有原子性，不可再分），基于标签，我们可以很容易地进行两组数据的相似度比较。
优点：标签的频率以及相对的位置关系确实一定程度可以表示出重要性和时序关系。
缺点：中文编辑距离（时序关系），余弦相似度（标签重要性）,他们没有直接的连接。
本项目基于jieba分词。

import jieba
str1=jieba.lcut(str1)
str2 = jieba.lcut(str2)

2.1中文编辑距离

编辑距离，又称Levenshtein距离（莱文斯坦距离也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作（插入，删除，替换）次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

2.1.1算法原理

假设我们可以使用d[ i , j ]个步骤（可以使用一个二维数组保存这个值），表示将串s[ 1…i ] 转换为 串t [ 1…j ]所需要的最少步骤个数，那么，在最基本的情况下，即在i等于0时，也就是说串s为空，那么对应的d[0,j] 就是 增加j个字符，使得s转化为t，在j等于0时，也就是说串t为空，那么对应的d[i,0] 就是 减少 i个字符，使得s转化为t。

然后我们考虑一般情况，加一点动态规划的想法，我们要想得到将s[1..i]经过最少次数的增加，删除，或者替换操作就转变为t[1..j]，那么我们就必须在之前可以以最少次数的增加，删除，或者替换操作，使得现在串s和串t只需要再做一次操作或者不做就可以完成s[1..i]到t[1..j]的转换。所谓的“之前”分为下面三种情况：

1. 我们可以在k个操作内将 s[1…i] 转换为 t[1…j-1]
2. 我们可以在k个操作里面将s[1..i-1]转换为t[1..j]
3. 我们可以在k个步骤里面将 s[1…i-1] 转换为 t [1…j-1]

针对第1种情况，我们只需要在最后将 t[j] 加上s[1..i]就完成了匹配，这样总共就需要k+1个操作。

针对第2种情况，我们只需要在最后将s[i]移除，然后再做这k个操作，所以总共需要k+1个操作。

针对第3种情况，我们只需要在最后将s[i]替换为 t[j]，使得满足s[1..i] == t[1..j]，这样总共也需要k+1个操作。而如果在第3种情况下，s[i]刚好等于t[j]，那我们就可以仅仅使用k个操作就完成这个过程。

最后，为了保证得到的操作次数总是最少的，我们可以从上面三种情况中选择消耗最少的一种最为将s[1..i]转换为t[1..j]所需要的最小操作次数。

2.1.2代码实现

#其中的str1，str2是分词后的标签列表
def edit_similar(str1,str2):
    len_str1=len(str1)
    len_str2=len(str2)
    taglist=np.zeros((len_str1+1,len_str2+1))
    for a in range(len_str1):
        taglist[a][0]=a
    for a in range(len_str2):
        taglist[0][a] = a
    for i in range(1,len_str1+1):
        for j in range(1,len_str2+1):
            if(str1[i - 1] == str2[j - 1]):
                temp = 0
            else:
                temp = 1
            taglist[i][j] = min(taglist[i - 1][j - 1] + temp, taglist[i][j - 1] + 1, taglist[i - 1][j] + 1)
    return 1-taglist[len_str1][len_str2] / max(len_str1, len_str2)

2.2基于词频的余弦相似度（TF-IDF）

余弦相似度：计算两者空间向量的夹角来表示两者的相似性。

2.2.1算法原理

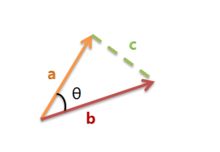
上图是向量a和向量b以及它们的夹角θ。根据初等数学公式，假设向量a、b的坐标分别为(x1,y1)、(x2,y2) ，则：

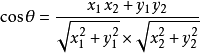
假设a是str1的标签特征向量，b是str2的标签特征向量，那么两者的相似度可以用cosθ表示，且0<=cosθ<=1。
而关于str1，str2的标签特征向量的获取，我们这里用了TF-IDF中的思想，利用词频来表示。
例如str1=[“我”,”爱”,”漫威”]，str2=[“我”,”喜欢”,”漫威”,”电影”]
则所有词语的集合为[“我”,”爱”,”喜欢”,”漫威”,”电影”]
str1（计算相应词频）转变后的a=[1,1,0,1,0]
str2（计算相应词频）转变后的b=[1,0,1,1,1]
计算后的相似度为：0.577350

2.2.2代码实现

#其中的str1，str2是分词后的标签列表
def cos_sim(str1, str2):
    co_str1 = (Counter(str1))
    co_str2 = (Counter(str2))
    p_str1 = []
    p_str2 = []
    for temp in set(str1 + str2):
        p_str1.append(co_str1[temp])
        p_str2.append(co_str2[temp])
    p_str1 = np.array(p_str1)
    p_str2 = np.array(p_str2)
    return p_str1.dot(p_str2) / (np.sqrt(p_str1.dot(p_str1)) * np.sqrt(p_str2.dot(p_str2)))

2.3Python difflib

difflib为python的标准库模块，无需安装。作用为对比文本之间的差异。关于该方法在python的官方文档中描述如下：
This is a flexible class for comparing pairs of sequences of any type, so long as the sequence elements are hashable. The basic algorithm predates, and is a little fancier than, an algorithm published in the late 1980’s by Ratcliff and Obershelp under the hyperbolic name “gestalt pattern matching.” The idea is to find the longest contiguous matching subsequence that contains no “junk” elements (the Ratcliff and Obershelp algorithm doesn’t address junk). The same idea is then applied recursively to the pieces of the sequences to the left and to the right of the matching subsequence. This does not yield minimal edit sequences, but does tend to yield matches that “look right” to people.
如上，来源于gestalt pattern matching，根据描述可以看出，该算法是类似于编辑距离的一种算法。

---

2.3.1代码实现

#其中的str1，str2并未分词，是两组字符串
diff_result=difflib.SequenceMatcher(None,str1,str2).ratio()

3.0加权三种算法

最终的字符串比较函数compare是由0.4倍的余弦相似度，0.3倍的编辑距离相似度，0.3倍的序列化匹配加权而成。
因为上文提到，序列化匹配和编辑距离相似度算法很相像，他们只考虑了时序关系，两者共同所占比例不应该过高。
最终代码如下：

def compare(str1, str2):
    if str1 == str2:
        return 1.0
    #其中的str1，str2并未分词，是两组字符串
    diff_result=difflib.SequenceMatcher(None,str1,str2).ratio()
    #分词
    str1=jieba.lcut(str1)
    str2 = jieba.lcut(str2)
    cos_result=cos_sim(str1, str2)
    edit_reslut=edit_similar(str1,str2)
    return cos_result*0.4+edit_reslut*0.3+0.3*diff_result

中文文本情感极性分析

情感极性分析是对带有情感色彩的主观性文本的分析、处理、归纳和推理的过程。按照处理文本可以分为基于新闻评论和产品的情感分析；按照作用可以分为舆情监控和信息预测。

• 利用情感词典

• 利用词向量和深度学习

github传送门：https://github.com/gongpx20069/DIYNLP

---

1.1利用情感词典

情感词典来源于Boson

该情感词典是从社交媒体中获得。
但是情感词典具有很大的局限性，语言的多义性和时序关系没有考虑，但基本可以对简单的文本进行正负向的评分。
考虑到该词典不会对词典中没有出现的词进行评分，对文本进行停用词处理没有什么意义，直接进行运算即可。

1.1.1模型导入代码

import jieba
import json
import os
SAdic={}
with open(os.path.join(os.getcwd(),"DIYNLP/model/SA.model"),"r") as f:
    SAdic=json.loads(f.read())
def getscore(str0):
    score = 0
    for i in jieba.lcut(str0):
        if i in SAdic.keys():
            score+=SAdic[i]
    return score

1.2利用词向量和深度学习

由于缺少训练集，等待后续探索……

参考文档：
[1] https://www.cnblogs.com/liangjf/p/8283519.html
[2] https://www.jianshu.com/p/4cfcf1610a73?nomobile=yes