python实现之K-均值聚类
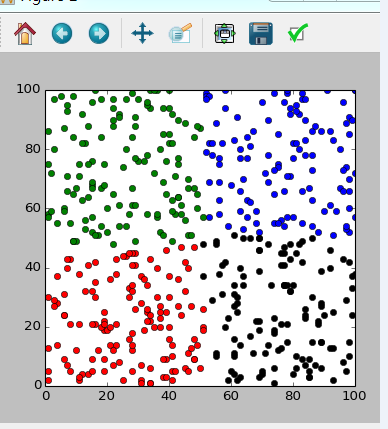
利用python写出一个二维数据模拟器,例如生成500个点。利用k-均值和k-中心点聚类技术对这500个点进行聚类分析。k=4。给出相应的核心代码和实验结果截屏。
解题思路:产生500个二维随机点,从数据集中选择随机选择K个值作为初始簇中心,根据每个点与各个簇中心的欧氏距离,将它分配到最相似的簇,不断迭代,直到类中所有对象和形心c(i)之间的误差的平方和保持不变,分配稳定,迭代结束,输出分类结果。
#########################################################################
#算法:k_均值,用于划分的K_均值算法,其中每个簇的中心都用簇中所有对象的均值来表示
#输入:
# k:簇的数目
# data_points:数据集
#输出:k个簇的集合
##########################################################################
import random
import numpy as np
import matplotlib.pyplot as plt
#产生500个二维随机点
def gene_data_points():
data_points=[]
for i in range(0,500):
gene_point=[random.randint(1,100),random.randint(1,100)]
data_points.append(gene_point)
return data_points
#print gene_data_point()
#根据分类结果产生中心点
def midpoint(class_point):
b=[0,0]
#将二维列表转化为向量,对应位置数字进行加法,除法运算
for i in class_point:
i=np.array(i)
b=b+i
b1=list(np.array(b)/float(len(class_point)))
return b1
#根据簇中对象的均值(中心点),将每个对象分配到最相似的簇
def update_cluster(data_points,k):
iter_num=0 #迭代次数
k_class=[] #分类的结果添加到k_class中
E=[]#类中所有对象和形心c(i)之间的误差的平方和
#根据k产生对应的二维列表
for i in range(0,k):
k_class.append([])
while iter_num>=0:
class_center=[] #k个类的中心点
if iter_num==0:
#可以从数据集中选择K个值作为初始簇中心
ran_point=random.sample(data_points,k)
for i in range(0,k):
k_class[i].append(ran_point[i])
#这里选取的是数据集中的前k个数作为初始簇中心
#for i in range(0,k):
# k_class[i].append(data_points[i])
for i in range(0,k):
class_center.append(midpoint(k_class[i]))
for i in range(0,k):
k_class[i]=[]
each_dist=[] #每个点和中心点的距离
for i in range(0,len(data_points)):
compare_dist=[]
for j in range(0,k):
dist=round(np.linalg.norm(data_points[i]-np.array(class_center[j])),1)
compare_dist.append(dist)
#根据每个点与各个簇中心的欧氏距离,将它分配到最相似的簇
for a in range(0,len(compare_dist)):
if(np.min(compare_dist)==compare_dist[a]):
k_class[a].append(data_points[i])
each_dist.append(compare_dist[a])
E.append(np.sum(each_dist))
#代表分配稳定,即本轮形成的簇与前一轮形成的簇相同,此时迭代结束
if iter_num!=0 and E[-2]==E[-1]:
break
iter_num+=1 #k_均值算法
#print E
return k_class
def raw_data(data_points): #画出原始数据
x=[]
y=[]
plt.figure(1)
for i in range(0,len(data_points)):
x.append(data_points[i][0])
y.append(data_points[i][1])
plt.xlim(xmax=100,xmin=0)
plt.ylim(ymax=100,ymin=0)
plt.plot(x,y,'or')
return 'this is random 500 data points'
#打印输出结果、画图
def display_class(k_class,k):
mark = ['or', 'ob', 'og', 'ok','sb', 'db', '