【模型评估】k折交叉验证和sklearn运用实战(cross validation)
k折交叉验证(cross validation)
留一法是特殊的k折交叉验证。k折交叉验证主要用于判断是否过拟合。k折交叉验证一般采用分层采样法取得训练集和验证集。分层采样是指,每个类按照比例在总体中随机取数据。
k折交叉验证(cross validation)实例
这是之前用过的逻辑回归的例子,重点放在后面的交叉验证上。
用sklearn中的数据集iris
导入需要的包
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (brier_score_loss, precision_score, recall_score,f1_score)
from sklearn.model_selection import learning_curve
import numpy as np
import matplotlib.pyplot as plt
取出需要的数据,其中iris_X有4个属性,共有150个样本点,iris_y的取值有3个,分别是0,1,2
iris = load_iris()
iris_X = iris.data #x有4个属性,共有150个样本点
iris_y = iris.target #y的取值有3个,分别是0,1,2
print(iris_X.size)
print(iris_X)
print(iris_y)
将所有的数据分为测试集和训练集,训练集有420个点
X_train, X_test, y_train, y_test = train_test_split(iris_X, iris_y, test_size=0.3)
print(X_train.size)
选择逻辑回归作为分类器
clf = LogisticRegression(random_state=0, solver=''newton-cg', multi_class='multinomial')
训练模型,这里计算出参数 w k , b w_k,b wk,b,输出 w k , b w_k,b wk,b
clf.fit(X_train, y_train)
print(clf.coef_)
print(clf.intercept_)
输出的结果,因为有3个类4个属性,所以结果如下
array([[-0.38846157, 0.82339943, -2.27459159, -0.96947549],
[ 0.40856593, -0.33711044, -0.09719451, -0.8815054 ],
[-0.02010436, -0.48628899, 2.3717861 , 1.8509809 ]])
array([ 8.94843505, 2.22587311, -11.17430816])
在测试集合上做预测,输出预测的类和正确的类
y_pred = clf.predict(X_test)
print(clf.predict(X_test))
print(y_test)
输出准确率、召回率、F1测度,由于是多分类,不是二分类,因此需要加average=“micro”
print("\tPrecision: %1.3f" % precision_score(y_test, y_pred, average="micro"))
print("\tRecall: %1.3f" % recall_score(y_test, y_pred, average="micro"))
print("\tF1: %1.3f\n" % f1_score(y_test, y_pred, average="micro"))
k折交叉验证,模型可视化。这里train_sizes=[0.1, 0.25, 0.5, 0.75, 1]是指,按总体比例的[0.1, 0.25, 0.5, 0.75, 1]取数据,
用 于 训 练 和 验 证 的 样 本 个 数 = [ 15 , 37.5 , 75 , 112.5 , 150 ] 用于训练和验证的样本个数=[15,37.5,75,112.5,150] 用于训练和验证的样本个数=[15,37.5,75,112.5,150],
由于 k = 10 k=10 k=10,
用 于 验 证 的 样 本 个 数 = [ 1.5 , 3.75 , 7.5 , 11.25 , 15 ] 用于验证的样本个数=[1.5,3.75,7.5,11.25,15] 用于验证的样本个数=[1.5,3.75,7.5,11.25,15],
用 于 训 练 的 样 本 个 数 = [ 15 , 37.5 , 75 , 112.5 , 150 ] − [ 1.5 , 3.75 , 7.5 , 11.25 , 15 ] 用于训练的样本个数=[15,37.5,75,112.5,150]-[1.5,3.75,7.5,11.25,15] 用于训练的样本个数=[15,37.5,75,112.5,150]−[1.5,3.75,7.5,11.25,15]
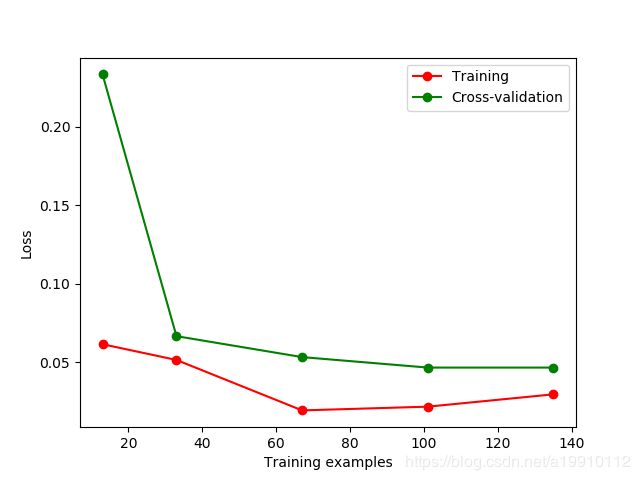
如图所示横坐标为用于训练的样本个数。
X_train, X_test, y_train, y_test = train_test_split(iris_X, iris_y, test_size=0.0)
train_sizes, train_loss, test_loss = learning_curve( clf, X_train, y_train, cv=10,
train_sizes=[0.1, 0.25, 0.5, 0.75, 1])
train_loss_mean = 1-np.mean(train_loss, axis=1)
test_loss_mean = 1-np.mean(test_loss, axis=1)
plt.plot(train_sizes, train_loss_mean, 'o-', color="r",
label="Training")
plt.plot(train_sizes, test_loss_mean, 'o-', color="g",
label="Cross-validation")
plt.xlabel("Training examples")
plt.ylabel("Loss")
plt.legend(loc="best")
plt.show()
以下是三次运行的结果图,每次运行输出的结果不同,可能是因为X_train, X_test, y_train, y_test = train_test_split(iris_X, iris_y, test_size=0.0)这里取的X_train有随机性。从图中可以看出,随着训练样本个数的增加,模型的交叉熵逐渐变小,也就是在未知数据集上的误差变小,模型的泛化能力逐渐增强。



加入标准化后的结果(normalization)
将数据集的四个属性全部都缩放到均值为0,方差为1的范围内,代码如下。
from sklearn import preprocessing
iris_X_std = preprocessing.scale(iris_X) #normalization