台大林轩田《机器学习基石》:作业一python实现
台大林轩田《机器学习基石》:作业一python实现
台大林轩田《机器学习基石》:作业二python实现
台大林轩田《机器学习基石》:作业三python实现
台大林轩田《机器学习基石》:作业四python实现
完整代码:
https://github.com/xjwhhh/LearningML/tree/master/MLFoundation
欢迎follow和star
在学习和总结的过程中参考了不少别的博文,且自己的水平有限,如果有错,希望能指出,共同学习,共同进步
##15
下载训练数据,每一行都是一个训练实例,每一行的数据中,前四项是特征值,最后一项是标签,编写PLA算法进行分类,设w初始为0,sign(0)=-1,问迭代多少次后算法结束?
1.需要自己手动添加一维特征,X0=1
2.一个点分类正确的条件是xwy>0(PLA)
3.算法结束的条件是所有实例都被分配正确
代码如下:
import numpy
class NaiveCyclePLA(object):
def __init__(self, dimension, count):
self.__dimension = dimension
self.__count = count
# get data
def train_matrix(self, path):
training_set = open(path)
x_train = numpy.zeros((self.__count, self.__dimension))
y_train = numpy.zeros((self.__count, 1))
x = []
x_count = 0
for line in training_set:
# add 1 dimension manually
x.append(1)
for str in line.split(' '):
if len(str.split('\t')) == 1:
x.append(float(str))
else:
x.append(float(str.split('\t')[0]))
y_train[x_count, 0] = int(str.split('\t')[1].strip())
x_train[x_count, :] = x
x = []
x_count += 1
return x_train, y_train
def iteration_count(self, path):
count = 0
x_train, y_train = self.train_matrix(path)
w = numpy.zeros((self.__dimension, 1))
# loop until all x are classified right
while True:
flag = 0
for i in range(self.__count):
if numpy.dot(x_train[i, :], w)[0] * y_train[i, 0] <= 0:
w += y_train[i, :] * x_train[i, :].reshape(5, 1)
count += 1
flag = 1
if flag == 0:
break
return count
if __name__ == '__main__':
perceptron = NaiveCyclePLA(5, 400)
print(perceptron.iteration_count("hw1_15_train.dat"))
运行了45次
##16
由于样本的排列顺序不同,最终完成PLA分类的迭代次数也不同。这道题要求我们打乱训练样本的顺序,进行2000次PLA计算,得到平均迭代次数。
只要在15题的基础上对训练样本进行打乱即可,使用random.shuffle(random_list)
代码如下:
import numpy
import random
class RandomPLA(object):
def __init__(self, dimension, count):
self.__dimension = dimension
self.__count = count
def random_matrix(self, path):
training_set = open(path)
random_list = []
x = []
x_count = 0
for line in training_set:
x.append(1)
for str in line.split(' '):
if len(str.split('\t')) == 1:
x.append(float(str))
else:
x.append(float(str.split('\t')[0]))
x.append(int(str.split('\t')[1].strip()))
random_list.append(x)
x = []
x_count += 1
random.shuffle(random_list)
return random_list
def train_matrix(self, path):
x_train = numpy.zeros((self.__count, self.__dimension))
y_train = numpy.zeros((self.__count, 1))
random_list = self.random_matrix(path)
for i in range(self.__count):
for j in range(self.__dimension):
x_train[i, j] = random_list[i][j]
y_train[i, 0] = random_list[i][self.__dimension]
return x_train, y_train
def iteration_count(self, path):
count = 0
x_train, y_train = self.train_matrix(path)
w = numpy.zeros((self.__dimension, 1))
while True:
flag = 0
for i in range(self.__count):
if numpy.dot(x_train[i, :], w)[0] * y_train[i, 0] <= 0:
w += y_train[i, 0] * x_train[i, :].reshape(5, 1)
count += 1
flag = 1
if flag == 0:
break
return count
if __name__ == '__main__':
sum = 0
for i in range(2000):
perceptron = RandomPLA(5, 400)
sum += perceptron.iteration_count('hw1_15_train.dat')
print(sum / 2000.0)
运行了40次左右
#17
与16题的区别就是在更新w时,多了一个参数,只需要更改iteration_count(self, path)方法
def iteration_count(self, path):
count = 0
x_train, y_train = self.train_matrix(path)
w = numpy.zeros((self.__dimension, 1))
while True:
flag = 0
for i in range(self.__count):
if numpy.dot(x_train[i, :], w)[0] * y_train[i, 0] <= 0:
# 添加参数的地方
w += 0.5 * y_train[i, 0] * x_train[i, :].reshape(5, 1)
count += 1
flag = 1
if flag == 0:
break
return count
运行了40次左右
##18
首先分别从题目中写的两个网址中下载训练样本和测试样本,然后运行pocket算法,每次迭代50次,共运行2000次,计算它对测试样本的平均错误率
1.和PLA算法的区别是,pocket算法每次对w进行更新直到达到迭代次数,每次更新w后都判断该线是否是当前最好的那条线,如果是就放入口袋,最终得到一条线
2.pocket算法的终止条件是达到了预设的更新次数
代码如下:
import numpy
import random
import copy
class Pocket(object):
def __init__(self, dimension, train_count, test_count):
self.__dimension = dimension
self.__train_count = train_count
self.__test_count = test_count
def random_matrix(self, path):
training_set = open(path)
random_list = []
x = []
x_count = 0
for line in training_set:
x.append(1)
for str in line.split(' '):
if len(str.split('\t')) == 1:
x.append(float(str))
else:
x.append(float(str.split('\t')[0]))
x.append(int(str.split('\t')[1].strip()))
random_list.append(x)
x = []
x_count += 1
random.shuffle(random_list)
return random_list
def train_matrix(self, path):
x_train = numpy.zeros((self.__train_count, self.__dimension))
y_train = numpy.zeros((self.__train_count, 1))
random_list = self.random_matrix(path)
for i in range(self.__train_count):
for j in range(self.__dimension):
x_train[i, j] = random_list[i][j]
y_train[i, 0] = random_list[i][self.__dimension]
return x_train, y_train
def iteration(self, path):
count = 0
x_train, y_train = self.train_matrix(path)
w = numpy.zeros((self.__dimension, 1))
best_count = self.__train_count
best_w = numpy.zeros((self.__dimension, 1))
# pocket算法,对一条线进行修改(最多50次),每次修改后都用训练集数据看是否是当前最好的那条线
for i in range(self.__train_count):
if numpy.dot(x_train[i, :], w)[0] * y_train[i, 0] <= 0:
w += 0.5 * y_train[i, 0] * x_train[i, :].reshape(5, 1)
# 修改次数加一
count += 1
num = 0
# 验证
for j in range(self.__train_count):
if numpy.dot(x_train[j, :], w)[0] * y_train[j, 0] <= 0:
num += 1
if num < best_count:
best_count = num
best_w = copy.deepcopy(w)
if count == 50:
break
return best_w
def test_matrix(self, test_path):
x_test = numpy.zeros((self.__test_count, self.__dimension))
y_test = numpy.zeros((self.__test_count, 1))
test_set = open(test_path)
x = []
x_count = 0
for line in test_set:
x.append(1)
for str in line.split(' '):
if len(str.split('\t')) == 1:
x.append(float(str))
else:
x.append(float(str.split('\t')[0]))
y_test[x_count, 0] = (int(str.split('\t')[1].strip()))
x_test[x_count, :] = x
x = []
x_count += 1
return x_test, y_test
# 验证
def test_error(self, train_path, test_path):
w = self.iteration(train_path)
x_test, y_test = self.test_matrix(test_path)
count = 0.0
for i in range(self.__test_count):
if numpy.dot(x_test[i, :], w)[0] * y_test[i, 0] <= 0:
count += 1
return count / self.__test_count
if __name__ == '__main__':
average_error_rate = 0
for i in range(2000):
my_Pocket = Pocket(5, 500, 500)
average_error_rate += my_Pocket.test_error('hw1_18_train.dat', 'hw1_18_test.dat')
print(average_error_rate / 2000.0)
我的运行结果为0.13181799999999988
##19
不采用贪心算法,而是采用第50次迭代结果为最终曲线,运行2000次,求对测试样本的平均错误率
只要将iteration(self, path)里,更新w之后对是否是当前最佳分类的判断去掉,始终将最新的放入口袋就好了
def iteration(self, path):
count = 0
x_train, y_train = self.train_matrix(path)
w = numpy.zeros((self.__dimension, 1))
for i in range(self.__train_count):
if numpy.dot(x_train[i, :], w)[0] * y_train[i, 0] <= 0:
w += 0.5 * y_train[i, 0] * x_train[i, :].reshape(5, 1)
count += 1
if count == 50:
break
return w
我的运行结果为0.3678069999999999
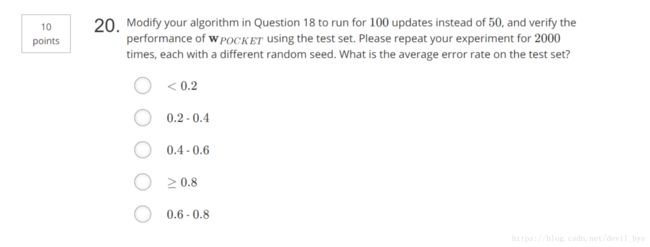
##20
如果把每次调用口袋算法的迭代次数从50次调为100次,求对测试样本的平均错误率
只需要将iteration(self, path)方法里判断是否达到规定迭代次数的常量设为100即可
def iteration(self, path):
count = 0
x_train, y_train = self.train_matrix(path)
w = numpy.zeros((self.__dimension, 1))
best_count = self.__train_count
best_w = numpy.zeros((self.__dimension, 1))
# pocket算法,对一条线进行修改(最多100次),每次修改后都用训练集数据看是否是当前最好的那条线
for i in range(self.__train_count):
if numpy.dot(x_train[i, :], w)[0] * y_train[i, 0] <= 0:
w += 0.5 * y_train[i, 0] * x_train[i, :].reshape(5, 1)
count += 1
num = 0
for j in range(self.__train_count):
if numpy.dot(x_train[j, :], w)[0] * y_train[j, 0] <= 0:
num += 1
if num < best_count:
best_count = num
best_w = copy.deepcopy(w)
if count == 100:
break
return best_w
我的运行结果为0.11375200000000021