[统计学习方法]感知机(Perceptron)算法（原始形式）的实例（例题求解）

例2.1 求解：
对正实例点 x1=(3,3)T，x2=(4,3)T， x 1 = ( 3 , 3 ) T ， x 2 = ( 4 , 3 ) T ， 负实例点 x3=(1,1)T x 3 = ( 1 , 1 ) T
解 构建最优化问题：

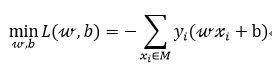
按照感知机学习算法的原始形式求解 w,b。η=1. w , b 。 η = 1.

（1）取初值 w0=[0,0]，b0=0 w 0 = [ 0 , 0 ] ， b 0 = 0
（2）对 x1=(3,3)T，y1(w0x1+b0)=0， x 1 = ( 3 , 3 ) T ， y 1 ( w 0 x 1 + b 0 ) = 0 ， 未能被正确分类，更新 w,b w , b

w1=(3,3)T←w0+ηy1x1 w 1 = ( 3 , 3 ) T ← w 0 + η y 1 x 1

b1=1←b0+ηy1 b 1 = 1 ← b 0 + η y 1

对 x1=(3,3)T，y1(w1x1+b1)>0, x 1 = ( 3 , 3 ) T ， y 1 ( w 1 x 1 + b 1 ) > 0 ,
对 x2=(4,3)T，y2(w1x2+b1)>0. x 2 = ( 4 , 3 ) T ， y 2 ( w 1 x 2 + b 1 ) > 0.

（3）对 x3=(1,1)T，y3(w1x3+b1)<0， x 3 = ( 1 , 1 ) T ， y 3 ( w 1 x 3 + b 1 ) < 0 ， 未能被正确分类，更新 w1,b1 w 1 , b 1

w2=(2,2)T←w1+ηy3x3 w 2 = ( 2 , 2 ) T ← w 1 + η y 3 x 3

b2=0←b1+ηy3 b 2 = 0 ← b 1 + η y 3

（4）对 x3=(1,1)T，y3(w2x3+b2)<0 x 3 = ( 1 , 1 ) T ， y 3 ( w 2 x 3 + b 2 ) < 0 ，未能被正确分类，更新 w2,b2 w 2 , b 2

w3=(1,1)T←w2+ηy3x3 w 3 = ( 1 , 1 ) T ← w 2 + η y 3 x 3

b3=−1←b2+ηy3 b 3 = − 1 ← b 2 + η y 3

（5）对 x3=(1,1)T，y3(w3x3+b3)<0 x 3 = ( 1 , 1 ) T ， y 3 ( w 3 x 3 + b 3 ) < 0 ，未能被正确分类，更新 w3,b3 w 3 , b 3

w4=(0,0)T←w3+ηy3x3 w 4 = ( 0 , 0 ) T ← w 3 + η y 3 x 3

b4=−2←b3+ηy3 b 4 = − 2 ← b 3 + η y 3

对 x3=(1,1)T，y3(w4x3+b4)>0. x 3 = ( 1 , 1 ) T ， y 3 ( w 4 x 3 + b 4 ) > 0.

（6）对 x1=(3,3)T，y1(w4x1+b4)<0， x 1 = ( 3 , 3 ) T ， y 1 ( w 4 x 1 + b 4 ) < 0 ， 未能被正确分类，更新 w4,b4 w 4 , b 4

w5=(3,3)T←w4+ηy1x1 w 5 = ( 3 , 3 ) T ← w 4 + η y 1 x 1

b5=−1←b4+ηy1 b 5 = − 1 ← b 4 + η y 1

对 x1=(3,3)T，y1(w5x1+b5)>0, x 1 = ( 3 , 3 ) T ， y 1 ( w 5 x 1 + b 5 ) > 0 ,
对 x2=(4,3)T，y2(w5x2+b5)>0. x 2 = ( 4 , 3 ) T ， y 2 ( w 5 x 2 + b 5 ) > 0.

（7）对 x3=(1,1)T，y3(w5x3+b5)<0， x 3 = ( 1 , 1 ) T ， y 3 ( w 5 x 3 + b 5 ) < 0 ， 未能被正确分类，更新 w5,b5 w 5 , b 5

w6=(2,2)T←w5+ηy3x3 w 6 = ( 2 , 2 ) T ← w 5 + η y 3 x 3

b6=−2←b5+ηy3 b 6 = − 2 ← b 5 + η y 3

（8）对 x3=(1,1)T，y3(w6x3+b6)<0， x 3 = ( 1 , 1 ) T ， y 3 ( w 6 x 3 + b 6 ) < 0 ， 未能被正确分类，更新 w6,b6 w 6 , b 6

w7=(1,1)T←w6+ηy3x3 w 7 = ( 1 , 1 ) T ← w 6 + η y 3 x 3

b7=−3←b6+ηy3 b 7 = − 3 ← b 6 + η y 3

对 x1=(3,3)T，y1(w7x1+b7)>0, x 1 = ( 3 , 3 ) T ， y 1 ( w 7 x 1 + b 7 ) > 0 ,
对 x2=(4,3)T，y2(w7x2+b7)>0. x 2 = ( 4 , 3 ) T ， y 2 ( w 7 x 2 + b 7 ) > 0.