分支限界法之单源最短路径
分支限界法通常是是广度优先或者以最小消耗(最大效益)优先的方式搜索问题的解控键树。
FIFO分支限界法
按照先进先出的原则选择下一个活结点作为扩展结点,即从节点中取出的顺序与加入结点的顺序相同。
分支限界法算法策略
(1活节点一旦成为扩展结点,就一次性产生其所有儿子结点
(2)在这些儿子结点中,导致不可行或者非最优解的儿子结点将会被舍弃,其余儿子结点加入活节点表中。
(3)从活结点表中取下一结点当做当前扩展结点,并重复上述结点扩展操作
这个过程一直持续到所需的解或者活节点表为空为止。
提高分支限界法的算法效率:
若我们把搜索过程看作是对一棵树的遍历,那么剪枝就是将树中一些"死结点"和不能得到最优解的结点剪掉。
实现分支限界法时,首先确定目标值上下界,边搜索边减掉搜索树的某些分支,提高搜索效率。在搜索时绝大部分需要用到剪枝。"剪枝"是搜索算法中优化程序的一种基本方法,需要通过设计出合理的判断方法,以决定某一分支的取舍。在设计判断方法的时候,需要遵循一定的原则
(1)正确性
剪枝的前提是一定要保证不丢失正确的结果。如果随便剪枝的,把带有最优解的那一部分支也剪掉的话,剪枝也就失去了意义。
(2)准确性
在保证正确性的基础上,采取合适的判断手段,是不包含最优解的枝叶尽可能多的被剪去,以达到优化程序的目的。
(3)高效性
设计优化程序的目的,是要减少搜索的次数,使程序运行的时间减少。但为了搜索的次数尽可能的少,我们又必须花功夫设计出一个准确性较高的优化算法,而当算法的准确性较高,其判断的次数势必增多,从而导致耗时增多。所以在优化和效率之间找到一个平衡点是关键。
单源最短路径问题
给定一个带权有向图G=(V,E),其中每条边的权是非负数。给定V中的一个顶点,成为源。现在要计算从源到所有其他个顶点的最短路径长度,这里路径长度指的是各边权之和。这个问题通常被称作单源最短路径问题。
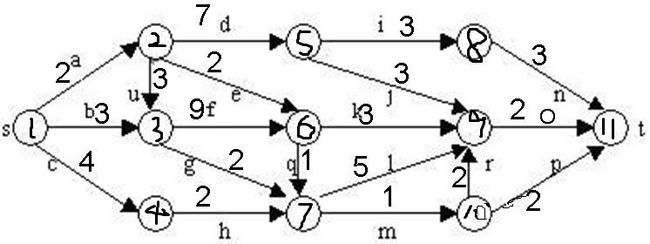
如图所示,每一边都有一非负权值。求图G到原点s的到t的最短路径。
算法分析
算法从G的源点s和空队列开始。结点s被扩展之后,他的儿子结点2,3,4倍一次插入队列当中。然后取出队头元素,进行下一步扩展。保证每一次扩展时,源到当前节点的和都是最小的。具体的解空间图如下:
算法过程
算法先从源节点s开始扩展,3个子结点2,3,4被插入到队列当中,如下图所示。
取出结点2,它有3个子树。结点2沿边f扩展到3时,路径长度为5,而结点3的当前路径为3(s->6),没有得到优化,该子树被剪掉。.结点2沿边d,e扩展值5,6时,将他们加入优先队列,如图
取出头结点3,它有两个子树。结点3沿f边扩展到结点6时,该路径长度为12,而结点6的当前路径为4,该路径没有被优化,该子树被剪枝。结点3沿g扩展到7时,将7加入到优先队列。如下如所示
重复上面操作直到队列为空。s到各个结点的最短路径。
代码如下:
#include
#include
using namespace std;
typedef struct ArcCell{
int adj;//保存权值
int info;//存储最短路径长度
}ArcCell,AdjMaxtrix[100][100];
typedef struct{
int data;
int length;
}VerType;
typedef struct{
VerType vexs[100];//顶点向量
AdjMaxtrix arcs;
int vexnum;//顶点数
int arcnum;//弧数
}Graph;
Graph G;
queue q;
void CreateGraph()
{
int m,n,t;
printf("输入顶点数和弧数:");
scanf("%d%d",&G.vexnum,&G.arcnum);
printf("输入顶点:");
for(int i=1;i<=G.vexnum;i++)
{
scanf("%d",&G.vexs[i].data);
G.vexs[i].length=10000;
}
for(int i=1;i<=G.vexnum;i++)
for(int j=1;j<=G.vexnum;j++)
{
G.arcs[i][j].adj=0;
}
printf("输入弧及权重:\n");
for(int i=1;i<=G.arcnum;i++)
{
scanf("%d%d%d",&m,&n,&t);
G.arcs[m][n].adj=1;
G.arcs[m][n].info=t;
}
}
int NextAdj(int v,int w)
{
for(int i=w+1;i<=G.vexnum;i++)
if(G.arcs[v][i].adj)
return i;
return 0;//not found;
}
void ShortestPaths(int v)
{
int k=0;//从首个节点开始访问
int t;
G.vexs[v].length=0;
q.push(G.vexs[v].data);
while(!q.empty())
{
t=q.front();
k=NextAdj(t,k);
while(k!=0)
{
if(G.vexs[t].length+G.arcs[t][k].info<=G.vexs[k].length)//减枝操作
{
G.vexs[k].length=G.vexs[t].length+G.arcs[t][k].info;
q.push(G.vexs[k].data);
}
k=NextAdj(t,k);
}
q.pop();
}
}
void Print()
{
for(int i=1;i<=G.vexnum;i++)
printf("%d------%d\n",G.vexs[i].data,G.vexs[i].length);
}
int main()
{
CreateGraph();
ShortestPaths(1);
Print();
return 0;
} 上面的代码只计算了到各个结点的最短路径值,并没有保存最小路径经过的节点。要求最短路径经过的节点可以采取逆推法。t的最短路径减去和它相连结点之间弧的权值,然后判断否相等,如果相等,则说明该节点在最短路径中,然后从该节点继续向前推,直到推导到t