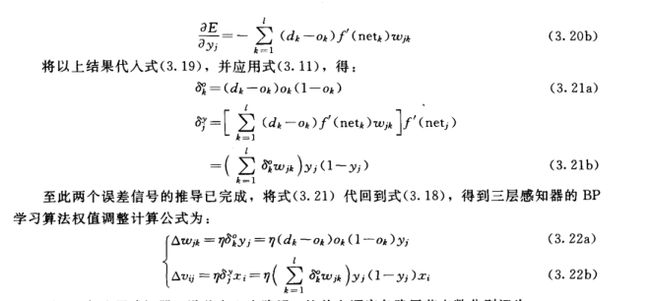机器学习与神经网络(四):BP神经网络的介绍和Python代码实现
前言:本篇博文主要介绍BP神经网络的相关知识,采用理论+代码实践的方式,进行BP神经网络的学习。本文首先介绍BP神经网络的模型,然后介绍BP学习算法,推导相关的数学公式,最后通过Python代码实现BP算法,从而给读者一个更加直观的认识。
1.BP网络模型
为了将理论知识描述更加清晰,这里还是引用《人工神经网络理论、设计及应用_第二版》相关的介绍。特别提醒一点:理解BP神经网络,最好提前阅读“感知器”的相关知识,相关资料可以查看前面的博文介绍。
以上公式都极其重要,因为我们将会在代码中用到他们,所以请理解并且牢记他们。
2.BP学习算法
BP学习算法是理解BP神经网络的核心内容,他解释了神经网络如何有效的去进行学习和权值调整。有兴趣的同学我希望可以认真阅读以下公式的推导(虽然看着吓人,但是并不是很难),这样能够更加深入的理解。当然,如果你想偷个懒,那你只要记住公式3.21a和3.21b、3.22a和3.22b及其含义就可以用代码实现它了,当然,千万别忘了前面刚刚学习的公式3.6-3.11。
3.BP神经网络的Python代码实现
以下代码的编写语言采用Python2.7版本,编译环境建议采用Anaconda,因为他自带了很多Python相关的包,非常方便。
下面的程序实现了一个图片上数字的识别功能:
首先我们看一下相关数据集的内容:
#! /usr/bin/env python
#coding=utf-8
from sklearn.datasets import load_digits#数据集
from sklearn.preprocessing import LabelBinarizer#标签二值化
from sklearn.cross_validation import train_test_split#数据集分割
import numpy as np
import pylab as pl#数据可视化
digits = load_digits()#载入数据
print digits.data.shape#打印数据集大小(1797L, 64L)
pl.gray()#灰度化图片
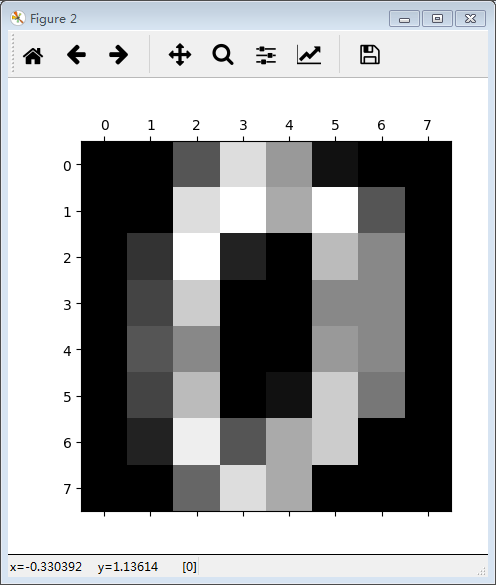
pl.matshow(digits.images[0])#显示第1张图片,上面的数字是0
pl.show()运行结果如下:
这里做一下说明,这个数据集大小为(1797,64),表示的是有1797张图片样本,其中的64,表示的是每一个样本包含64个特征,也就是上述图片所示,将8*8的矩阵排成一行,即64列。
接下来我们实现BP神经网络:
#! /usr/bin/env python
#coding=utf-8
from sklearn.datasets import load_digits#数据集
from sklearn.preprocessing import LabelBinarizer#标签二值化
from sklearn.cross_validation import train_test_split#数据集分割
import numpy as np
import pylab as pl#数据可视化
def sigmoid(x):#激活函数
return 1/(1+np.exp(-x))
def dsigmoid(x):#sigmoid的倒数
return x*(1-x)
class NeuralNetwork:
def __init__(self,layers):#这里是三层网络,列表[64,100,10]表示输入,隐藏,输出层的单元个数
#初始化权值,范围1~-1
self.V=np.random.random((layers[0]+1,layers[1]))*2-1#隐藏层权值(65,100),之所以是65,因为有偏置W0
self.W=np.random.random((layers[1],layers[2]))*2-1#(100,10)
def train(self,X,y,lr=0.1,epochs=10000):
#lr为学习率,epochs为迭代的次数
#为数据集添加偏置
temp=np.ones([X.shape[0],X.shape[1]+1])
temp[:,0:-1]=X
X=temp#这里最后一列为偏置
#进行权值训练更新
for n in range(epochs+1):
i=np.random.randint(X.shape[0])#随机选取一行数据(一个样本)进行更新
x=X[i]
x=np.atleast_2d(x)#转为二维数据
L1=sigmoid(np.dot(x,self.V))#隐层输出(1,100)
L2=sigmoid(np.dot(L1,self.W))#输出层输出(1,10)
#delta
L2_delta=(y[i]-L2)*dsigmoid(L2)#(1,10)
L1_delta=L2_delta.dot(self.W.T)*dsigmoid(L1)#(1,100),这里是数组的乘法,对应元素相乘
#更新
self.W+=lr*L1.T.dot(L2_delta)#(100,10)
self.V+=lr*x.T.dot(L1_delta)#
#每训练1000次预测准确率
if n%1000==0:
predictions=[]
for j in range(X_test.shape[0]):
out=self.predict(X_test[j])#用验证集去测试
predictions.append(np.argmax(out))#返回预测结果
accuracy=np.mean(np.equal(predictions,y_test))#求平均值
print('epoch:',n,'accuracy:',accuracy)
def predict(self,x):
#添加转置,这里是一维的
temp=np.ones(x.shape[0]+1)
temp[0:-1]=x
x=temp
x=np.atleast_2d(x)
L1=sigmoid(np.dot(x,self.V))#隐层输出
L2=sigmoid(np.dot(L1,self.W))#输出层输出
return L2
digits=load_digits()#载入数据
X=digits.data#数据
y=digits.target#标签
#print y[0:10]
#数据归一化,一般是x=(x-x.min)/x.max-x.min
X-=X.min()
X/=X.max()
#创建神经网络
nm=NeuralNetwork([64,100,10])
X_train,X_test,y_train,y_test=train_test_split(X,y)#默认分割:3:1
#标签二值化
labels_train=LabelBinarizer().fit_transform(y_train)
#print labels_train[0:10]
labels_test=LabelBinarizer().fit_transform(y_test)
print 'start'
nm.train(X_train,labels_train,epochs=20000)
print 'end'运行结果:
总结:本博文首先介绍了BP神经网络模型(3层神经网络为例),然后介绍BP学习算法以及公式推导,最后通过Python代码实现算法原理。当然,网上有一个非常典型的BP神经网络实现的例子:一个11行Python代码实现的神经网络,有兴趣的可以学习一下。
ps:如有错误之处,还请指正。