神经网络学习
神经网络
一、神经网络概述
人工神经网络是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。
神经网络的研究内容相当广泛,反映了多学科交叉技术领域的特点。主要的研究工作集中在以下几个方面:
(1)生物原型研究
从生理学、心理学、解剖学、脑科学、病理学等方面研究神经细胞、神经网络、神经系统的生物原型结构及其功能机理。
(2)建立理论模型
根据生物原型的研究,建立神经元、神经网络的理论模型。其中包括概念模型、知识模型、物理化学模型、数学模型等。
(3)网络模型与算法研究
在理论模型研究的基础上构作具体的神经网络模型,以实现计算机模拟或准备制作硬件,包括网络学习算法的研究。
1.神经元模型
M-P神经元模型:神经元接收来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值与神经元的阈值进行比较,然后通过激活函数(activation function)处理以产生神经元的输出。
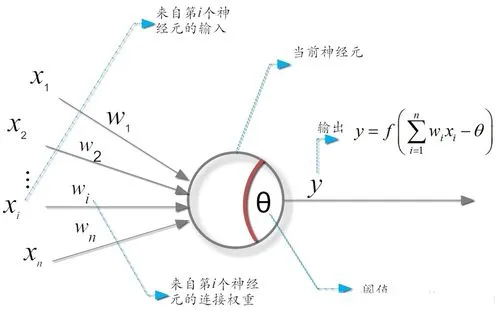
2.感知器与多层网络
感知器(Perceptron)由两层神经元组成,输入层接收外界输入信号后传递给输出层,输出层是M-P神经元。
感知器能容易地实现逻辑与、或、非运算。
感知器只有输出层神经元进行激活函数处理,即只拥有一层功能神经元(functional neuron),其学习能力非常有限。上述与、或、非问题都是线性可分(linearly separable)问题,即存在一个线性超平面能将他们分开。
而对于异或等非线性可分问题,需使用多层功能神经元。如输出层与输入层之间的一层神经元,被称为隐含层(hidden layer),隐含层和输出层神经元都是拥有激活函数的功能神经元。
多层前馈神经网络(multi-layer feedforward networks):每层神经元与下一层神经元全连接,神经元之间不存在同层连接,也不存在跨层连接。
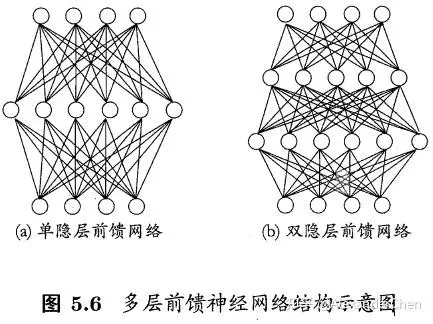
其中输入层神经元接受外界输入,隐含层和输出层神经元对信号进行加工,最后结果由输出层神经元输出。
只需包含隐藏层,即可称为多层网络。
神经网络的学习过程,就是根据训练数据来调整神经元之间的连接权(connection weight)以及每个功能神经元的阈值。
3.全局最小与局部最小
若用E表示神经网络在训练集上的误差,则其显然是关于连接权 w w w和阈值 θ \theta θ的函数。此时神经网络的训练过程可看做是一个参数寻优过程,即寻找一组最优参数使E最小。
我们会常谈到2钟最优,局部最小(local minimum)与全局最小(global minimum)
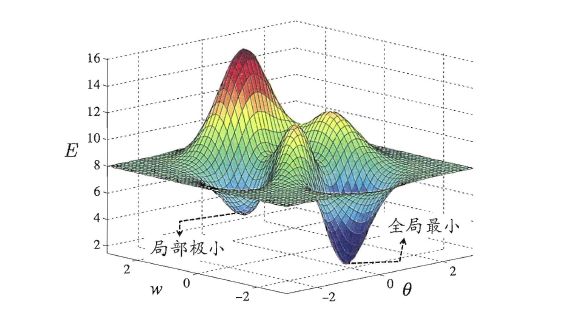
实际中,人们常采用以下策略跳出局部最小,从而进一步接近全局最小。
- 以多种不同参数初始化多个神经网络,按标准化方法训练后,取其中误差最小的解最为最终参数。
- 使用模拟退火(simulated annealing)算法。模拟退火在每一步以一定的概率接受比当前解更差的结果,从而有助于跳出局部最小。
- 使用随机梯度下降。随机梯度下降法在计算梯度时加入了随机因素,即便陷入局部极小点,计算出的梯度仍可能不为0,就有机会跳出局部极小继续搜索。
二、神经网络的特点
- 自适应性
自适应性指一个系统能改变自身的性能以适应环境变化的能力。当环境发生变化时,相当与给神经网络输入新的训练样本,网络能够自动调整结构参数并改变映射关系,从而对特定的输入产生相应的输出。 - 非线性
人工神经元处于激活或抑制状态,表现为数学上的非线性关系。 - 鲁棒性与容差性
神经网络具备信息存储的分布性,因此,局部的损害会使人工神经网络的运行适度减弱,但不会产生灾难性的错误。 - 计算的并行性与存储的分布性
每个神经元都可以根据接收到的信息进行独立的运算和处理,并输出结果。同一层中的不同神经元可以同时进行运算,然后传输到下一层进行处理。因此,神经网络往往能够发挥并行计算的优势,大大提升运算速度。 - 分布式存储
由于神经元之间的相互独立性,神经网络学习的“知识”没有集中存储在网络的某一处,而是分布在网络的所有连接权值中。
三、神经网络的应用
(1)模式分类
(2)聚类
聚类与分类不同,分类需要提供已知其正确类别的样本,进行有监督学习。聚类不需提供已知样本,完全根据给定样本进行工作,只需给定聚类的类别数n,网络就会自动按样本间的相似性将输入样本分为n类。
(3)回归与拟合
(4)优化计算
(5)数据压缩
四、神经网络的结构
1.前向网络
前向网络中的各个神经元接受前一级的输入并输出到下一级,网络中没有反馈,可以用一个有向无环图表示。
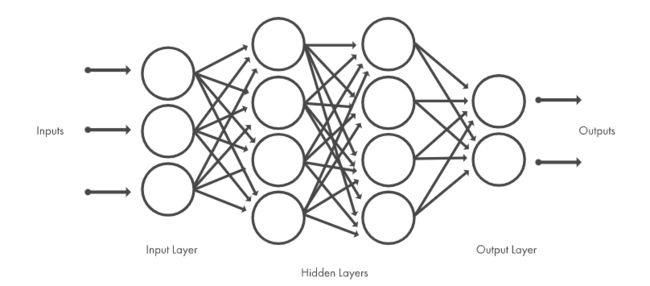
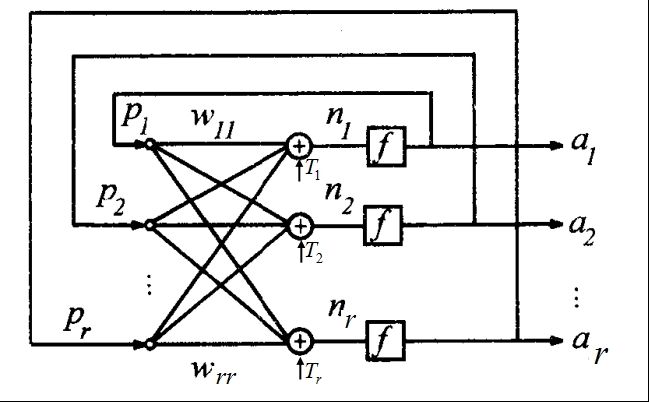
2.反馈网络
反馈网络内的神经元间有反馈,可以用一个无向的完备图表示。这种神经网络的信息处理是状态的变换,可以用动力学系统理论处理。系统的稳定性与联系记忆功能有密切的关系。
五、神经网络的学习方式
(1)有监督学习
有监督学习中的每个训练样本都有一个期望输出,网络在训练时计算实际输出与期望输出之间的误差,再根据误差的大小和方向对网络权值进行更新。这样的调整反复进行,直到误差达到预期的精度,整个网络形成了一个封闭的闭环系统。
有监督学习往往能有效完成模式分类、函数拟合等工作。
(2)无监督学习
在无监督学习中,网络只接收一系列的输入样本,只能凭借各输入样本之间的关系对权值进行更新。
无监督学习中研究最多、应用最广的是聚类
六、BP神经网络
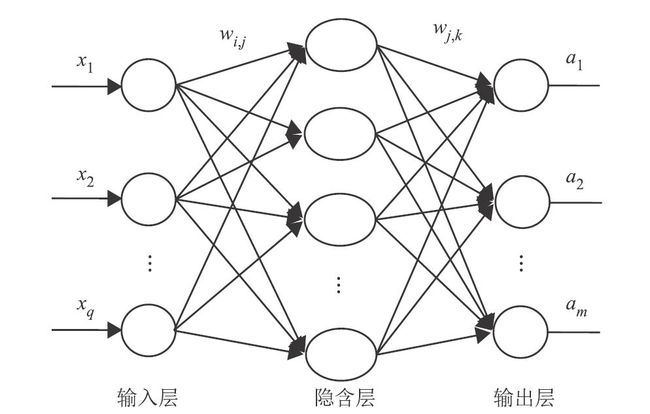
BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一。
1.BP神经网络的特点
(1)网络由多层构成,层与层之间全连接,同一层神经元之间无连接。
(2)BP神经网络的传递函数必须可微。BP神经网络一般使用Sigmoid函数或线性函数作为传递函数。
一个简单的Sigmoid函数可由下式确定:
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
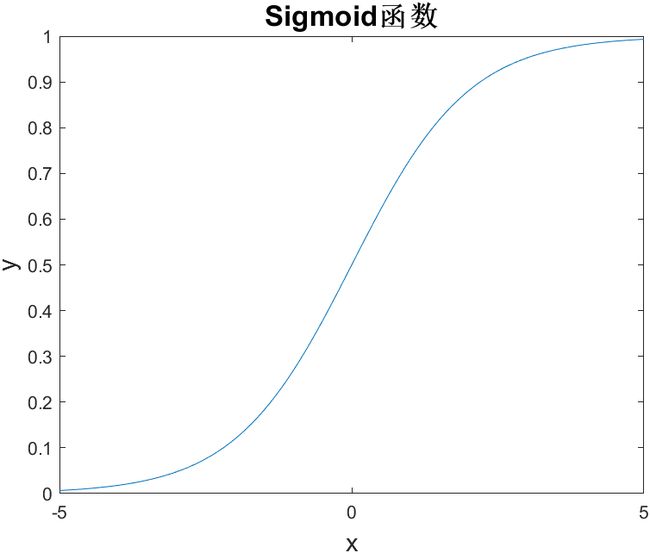
从图中可以看出,Sigmoid函数是光滑的、可微的函数,在分类时,它比线性函数更精确,容差性更好。
BP神经网络的典型设计是隐含层采用Sigmoid函数作为传递函数,输出层采用线性函数为传递函数。
(3)采用误差方向传播算法进行学习。在BP神经网络中,数据从输入层经隐含层逐层向后传播;在训练网络权值时,沿着减小误差的方向,从输出层经过中间层各层逐层向前修正网络的权值。随着学习的不断进行,最终的误差将越来越小。
2.BP神经网络的学习算法
BP算法工作流程:

BP算法的目标是最小化训练集D上的累计误差
E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E = 1 m ∑ k = 1 m E k E_k=\frac{1}{2}\sum^l_{j=1}(\hat{y}^k_j-y^k_j)^2 \\ E=\frac{1}{m}\sum^m_{k=1}E_k Ek=21j=1∑l(y^jk−yjk)2E=m1k=1∑mEk
[Hornik et al,1989]证明,一个包含足够多神经元的隐含层,多层前馈网络能一任意精度逼近任意复杂度的连续函数。然而,如何设置隐含层神经元的个数是个未决问题,实际中靠“试错法”(trial-by-error)调整。
3.BP神经网络的局限性
神经网络实现了一个从输入到输出的映射功能,具有实现任何复杂非线性映射的能力,特别适合求解内部机制复杂的能力,但BP神经网络也具有一些难以克服的局限性。
- 需要的参数较多,且对于参数的选择没有有效的方法。确定一个BP神经网络,需要知道网络的层数、每层的神经元个数和权值。网络权值依据训练样本和学习率经过学习得到。
- 容易陷入局部最优。实际应用中,BP算法可能经常陷入局部最小值。此时可通过改编初始值并多次运行的方式获得全局最优值;也可以改编算法,通过加入动量项,使连接权值以一定概率跳出局部最优点。
- 样本依赖性。网络模型的逼近和推广能力与学习样本的典型性密切相关。
- 初始权值敏感性。训练的第一步是给定一个较小的随机初始权值,由于权值是随机给定的,所以BP神经网络往往具有不可重现性。