决策树算法——机器学习(理论+图解+python代码)
前言
暑假打算吃透一本书叫《机器学习》,大家也亲切的叫它西瓜书,看完决策树这部分想做做总结,虽然几年前对决策树的知识就有点印象,但是我发现现在又有了很多新的收获。
一、基本流程
二、划分选择
三、剪枝处理
四、连续与缺失值
五、多变量决策树
六、房价数据集的决策树算法python实现
一、基本流程
决策树(decision tree)是一类常见的机器学习算法,它是基于树结构来进行决策的。
——“这是好瓜吗?”
——“它的颜色是青绿色的、根蒂是蜷缩的、敲声是......,所以结论是:这是个好瓜”。
以上,为了给好瓜坏瓜分类,我们要回答不同瓜的不同属性,来帮助我们判断。
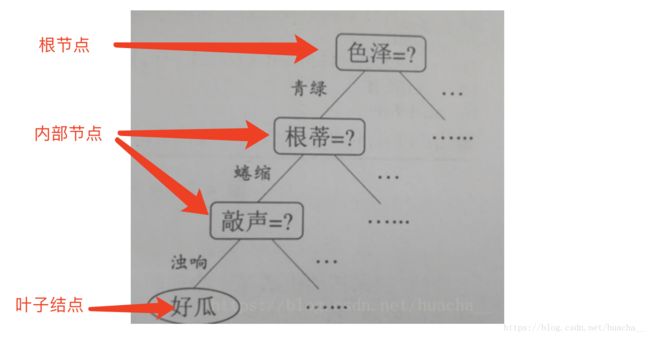
图1. 这是一棵决策树
叶子结点就对应我们的决策结果,其它的根节点和内部节点就对应于一个属性测试。决策树学习的目的就是为了产生一棵泛化能力强,即处理未见事例能力强的决策树。
二、划分选择
决策树学习的关键就是如何选择最优划分属性,也就是找到上面图中为什么要选择“色泽”属性作为根节点的理由,以及在接下来的划分中,为什么要选择该划分属性的理由。
1、信息增益
著名的ID3决策树学习算法就是以信息增益为准则来选择划分属性,下面这个图(不是西瓜的例子了,是我之前整理的,关于得病与否的例子)在14个样本中,yes=9个,no=5个,此时信息熵=-(9/14*log(9/14)+5/14*log(5/14))=0.940286,值得注意的是这里的对数是以2为底,下面随机选择一个属性比如年龄作为划分依据,分成<30,31~40,>40这三组,这三组中yes和no各占不同的数目,计算方式跟上面一样,得到0.97095,0,0.81这三个信息熵,然后成权重后相加得到0.57856,这跟没划分之前的信息熵相差0.361726,这就是信息增益的量。
对其它的属性我们也可以做同样的计算,把得到最大的信息增益的作为最优划分属性,这就是ID3算法选择划分属性的准则。
2、增益率
实际上,信息增益准则对可取值数目较多的属性有所偏好,为了减少这种偏好可能带来的不利影响,C4.5决策树算法不直接使用信息增益,而是使用增益率来选择最优划分属性。
这相当于在上面例子中的信息增益0.57856的基础上再除以-(5/14*log(5/14)+4/14*log(4/14)+5/14*log(5/14)),也就是对属性值d 的权重再求个熵,相除后作为最后的增益率。
需要注意的是,增益率准则对可取值数目较少对属性有所偏好。所以,C4.5算法并不是直接选择增益率最大对候选划分属性,而是用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
3、基尼指数
CART决策树算法使用基尼指数来选择划分属性,这个准则不再用熵和增益来衡量数据集的纯度,而是用基尼值来度量。直观来说这个值反映了从数据集中随机抽取两个样本,其类别标记不一致的概率。因此基尼值越小,则数据集的纯度越高。
三、剪枝处理
剪枝是决策树算法对付“过拟合”的主要手段,通过主动去掉一些分支来降低过拟合的风险。根据泛化性能是否提升来判断和评估要不要留下这个分支。
那么,如何判断决策树的泛化性能是否提升呢?可以采用“留出法”(一种性能评估方法),即预留一部分数据用作“验证集”来进行性能评估。
1、预剪枝
是否应该进行这个划分?预剪枝要对划分前和划分后的泛化性能进行估计。划分后的验证集精度如果比划分前的验证集精度高,那么,就决定划分,否则,预剪枝策略禁止这个结点被划分。
优点:预剪枝使得决策树的很多分支都没有展开,这不仅降低来过拟合的风险,还显著减少了决策树的训练时间开销和测试时间的开销。
缺点:预剪枝基于“贪心”的本质,禁止这些分支展开,给预剪枝决策树带来来欠拟合的风险。
2、后剪枝
后剪枝先从训练集上生成一棵完整的树,从最后一个分支来判断要不要剪枝。下面是根据训练集生成的一整棵树:
后剪枝策略通常比预剪枝策略保留更多的分支。一般情况下,后剪枝决策树的欠拟合风险很小,泛化能力往往优于预剪枝决策树,但是它的训练时间开销比未剪枝决策树和预剪枝决策树都要大的多。
四、连续与缺失值
1、连续值处理
以上的属性值都是离散的,现实中通常会遇到连续的属性值。这个时候,连续属性离散化技术就可以用上啦,C4.5决策树算法采用的是最简单的策略二分法来对连续值进行处理。给西瓜属性考虑密度的属性,首先把不同样本的密度值按照从小到大排序,然后找到候选划分点,把每个候选划分点的信息增益算出来,取max的值作为密度的信息增益。第二次max就是找到最优划分属性了。
这里需要注意的是,与离散属性值不同,若当前结点划分属性为连续的,那么该属性还可以作为后面结点的划分属性。
2、缺失值处理
如果样本中有缺失值,那么会产生以下两个问题:
(1)如何在属性值缺失的情况下计算属性的信息增益,从而进行划分属性的选择?
(2)给定划分属性,如果样本在该属性值上是缺失的,如何对这个样本进行划分?
针对(1)的处理非常简单,假设17个样本在“色泽”属性上只有14个是有值的,另外3个是缺失的,那么就以这14个样本的属性值计算信息增益,然后把这个值乘以14/17,相当于乘上一个权重,当作这全部17个样本的信息增益。然后进行后续的属性划分。
针对(2)的处理也很简单,本来每个样本在结点中的权重都是1,当样本「8」在“纹理”上出现缺失值,那么在“纹理=清晰”、“纹理=模糊”、“纹理=稍糊”这三个分支中都会出现样本「8」,只是权重不再是1,而是7/15,5/15,3/15(这三个权重的来源是这三个分支中各个样本的比例,不包括这个样本「8」)
五、多变量决策树(*拓展)
以上的讲到的各种结点,都是单个的属性,有没有可能是多种属性的线性组合呢?看看下面这个两个图:
在多变量决策树中,非叶子结点不再是针对某个属性,而是对属性的线性组合进行测试,也就是说每一个非叶子结点就是一个线性分类器。(很6666)
六、房价数据集的决策树算法python实现
%matplotlib inline #jupyternotebook上需要这句
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets.california_housing import fetch_california_housing #sklearn中自带数据集
housing = fetch_california_housing()
print(housing.DESCR)
print(housing.data.shape) #查看数据集形状
from sklearn import tree
dtr = tree.DecisionTreeRegressor(max_depth = 2)
#这个函数很重要,里面的参数有兴趣的同学可以查看sklearn官方文档,很强势
dtr.fit(housing.data[:, [6, 7]], housing.target)
#要可视化显示 首先需要安装 graphviz http://www.graphviz.org/Download..php
dot_data = \
tree.export_graphviz(
dtr,
out_file = None,
feature_names = housing.feature_names[6:8],
filled = True,
impurity = False,
rounded = True
)
#pip install pydotplus
import pydotplus
graph = pydotplus.graph_from_dot_data(dot_data)
graph.get_nodes()[7].set_fillcolor("#FFF2DD")
from IPython.display import Image
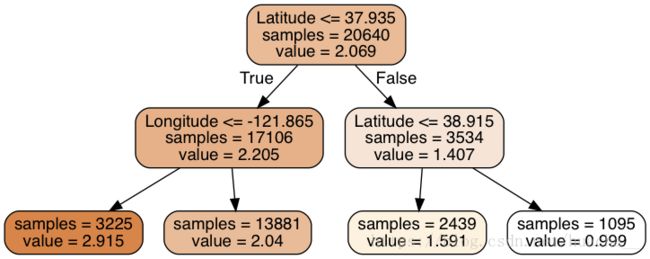
Image(graph.create_png())
输出如下:
#将数据划分成训练集和验证集,查看准确率
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test = \
train_test_split(housing.data, housing.target, test_size = 0.1, random_state = 42)
dtr = tree.DecisionTreeRegressor(random_state = 42)
dtr.fit(data_train, target_train)
dtr.score(data_test, target_test)输出如下:
0.637318351331017