【python数据预处理笔记】——特征缩放（标准化 & 归一化）

目 录

一、Q&A

Q1 什么是标准化、归一化、规范化、正则化？

A： 在特征缩放中，标准化和归一化是特征缩放的两种形式，一个是减去均值后再除以方差，一个是把数据压缩到 $[0,1]$ 或者 $[-1,1]$ 区间上。规范化是线性代数中的名词，在数据科学中也有人把特征缩放称为特征规范化或者特征归一化，不过为了避免混淆不建议这样做。而正则化是一种防止过拟合的手段，用来对模型的复杂度或者特征维度进行惩罚，严格来说不属于数据预处理的内容。

Q2 为什么需要做标准化或者归一化？

A： 当模型是输入特征的平滑函数时，那么它对输入的尺度是非常敏感的，取值范围大的特征被无意中赋予了更大的权重，它会压缩取值范围小的特征对结果的影响。例如 $y=x_1+x_2+7$ 是一个简单的线性函数，如果 $x_1$ 的尺度为 $[0,1]$ ，$x_2$ 的尺度为 $[0,10000]$ ，那么 $x_2$ 的变动将会产生更大的影响。这个时候就要对特征进行缩放，也就是标准化或者规范化。目的是使其不同尺度之间的特征具有可比性，同时不改变原始数据的分布。

Q3 什么样的模型需要输入标准化或者归一化的特征，什么样的模型不需要？

A： 正如前一问提到的，需要对特征进行标准化的模型是输入的平滑函数，比如线性回归模型、逻辑回归模型或者包含矩阵的模型。此外，k-均值聚类、k近邻法、径向基和函数，以及所有使用欧式距离的方法都属于这种情况。相对地，基于空间分割树的模型（决策树、梯度提升树、随机森林）对尺度是不敏感的。除非输入的尺度是随时间变化的，也就是说如果特征是某种累计值，那么它最终可能会超出训练树的取值范围。如果出现了这种情况，就必须定期地对输入尺度进行调整，或者使用区间计数法。

Q4 哪些数据不能做特征缩放？

A： 稀疏数据不能进行特征缩放，因为特征缩放相当于对原数据进平移和缩放。而对于稀疏数据来说，数据中含有大量的0，一旦进行平移，那么稀疏特征将会变为密集特征，这会产生很大的影响，比如特征向量中包含没有在文章中出现的所有单词，那么当它变为密集向量的时候，特征的意义会发生巨大的改变。

二、特征标准化/方差放缩

  特征标准化可用下面的公式来定义：

$$x^{\prime }=\frac{x-\mu }{\sigma }$$

其中 $\mu$ 和 $\sigma$ 是数据的均值和标准差。缩放后的特征均值为0，方差为1，尺度为原来的 $\frac{1}{\sigma }$ 。标准化依据相同的标准调整特征使之能互为参考有可比性。

好处：

1. 不改变原始数据的分布，保持各个特征维度对目标函数的影响权重
2. 对目标函数的影响体现在几何分布上
3. 在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景

三、特征归一化

1. min-max缩放

  min-max缩放的公式如下：

$$x^{\prime }=\frac{x-min(x)}{max(x)-min(x}$$

min-max缩放可以将数据压缩（或扩展）到 $[0,1$ 区间中。消除量纲对结果的影响，使不同特征之间具有可比性。

应用：

1. 无量纲化

  例如房子数量和收入，从业务层知道这两者的重要性一样，所以把它们全部归一化，这是从业务层面上作的处理。

2. 避免数值问题

  不同的数据在不同列数据的数量级相差过大的话，计算起来大数的变化会掩盖掉小数的变化。

3. 一些模型求解的需要

  例如梯度下降法，如果不归一化，当学习率较大时，求解过程会呈 Z 字形下降。学习率较小，则会产生直角形路线，不管怎么样，都不会是好路线。具体参考 神经网络为什么要归一化

4. 时间序列

  进行log分析时，会将原本绝对化的时间序列归一化到某个基准时刻，形成相对时间序列，方便排查。

5. 收敛速度

  加快求解过程中参数的收敛速度。

特点：

1. 对不同特征维度进行伸缩变换
2. 改变原始数据的分布（不改变单特征分布的形状），使得各个特征维度对目标函数的影响权重归于一致（使得扁平分布的数据伸缩变换成类圆形）
3. 对目标函数的影响体现在数值上
4. 把有量纲表达式变为无量纲表达式

好处：

1. 提高迭代求解的收敛速度
2. 提高迭代求解的精度

缺点：

1. 最大值与最小值非常容易受异常点影响
2. 鲁棒性较差，只适合传统精确小数据场景

2. L2归一化

  $l^2$归一化的公式如下：

$$x^{\prime }=\frac{x}{||x|{|}_2}$$

其中 $||x|{|}_2=\sqrt{(x_1^2+x_2^2+\cdots +x_m^2)}$ ，$l^2$归一化使得缩放后数据的尺度变为原来的 $\frac{1}{||x|{|}_2}$ ，在 $[-1,1]$ 之间。

3. 十进制归一化

  十进制归一化与L2-归一化类似，都是把数据规范到 $[-1,1]$ 区间内，其公式如下：

$$x^{\prime }=\frac{x}{10^j}$$

其中 $j$ 是使得 $max(x^{\prime })<1$ 的最小整数。

四、实例——不同缩放方法的对比

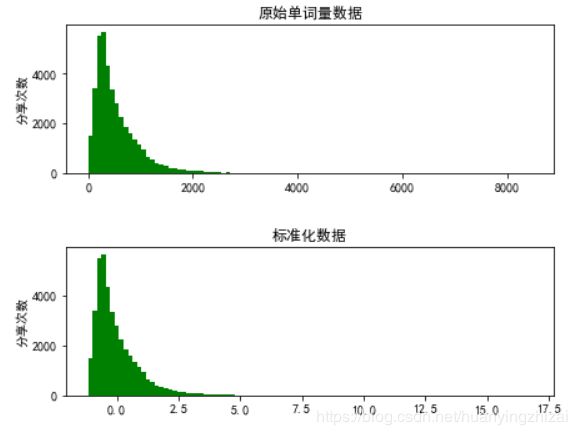
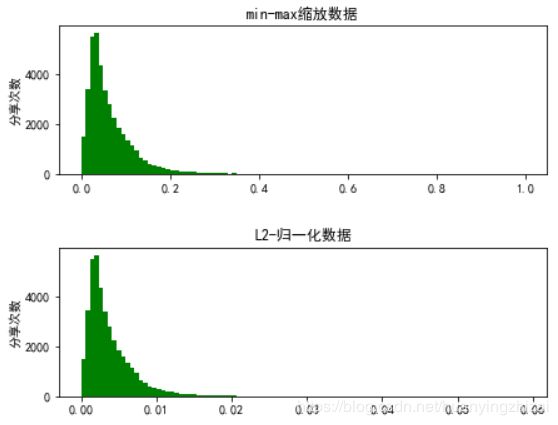
  我们对在线新闻流行度数据集中的文章单词量特征进行特征缩放，并观察其结果。

import pandas as pd
import sklearn.preprocessing as preproc

onp_df = pd.read_csv('data/OnlineNewsPopularity/OnlineNewsPopularity.csv')

# 标准化
onp_df['standardized_n'] = preproc.StandardScaler().fit_transform(onp_df[[' n_tokens_content']])

# min-max缩放
onp_df['minmax_n'] = preproc.minmax_scale(onp_df[[' n_tokens_content']])

# L2-归一化
onp_df['l2_normalized_n'] = preproc.normalize(onp_df[[' n_tokens_content']], axis = 0)

import matplotlib.pyplot as plt

fig,(ax1, ax2, ax3, ax4) = plt.subplots(4, 1, figsize = (7, 12))
plt.subplots_adjust(wspace =0, hspace =0.5)

ax1.hist(onp_df[' n_tokens_content'], bins = 100, color = 'g')
ax1.set_xlabel('')
ax1.set_ylabel('分享次数')
ax1.set_title('原始单词量数据')

ax2.hist(onp_df['standardized_n'], bins = 100, color = 'g')
ax2.set_xlabel('')
ax2.set_ylabel('分享次数')
ax2.set_title('标准化数据')

ax3.hist(onp_df['minmax_n'], bins = 100, color = 'g')
ax3.set_xlabel('')
ax3.set_ylabel('分享次数')
ax3.set_title('min-max缩放数据')

ax4.hist(onp_df['l2_normalized_n'], bins = 100, color = 'g')
ax4.set_xlabel('')
ax4.set_ylabel('分享次数')
ax4.set_title('L2-归一化数据')

plt.show()