[台大机器学习笔记整理]perceptron learning algorithm
Machine Learning的基本模型是
A takes D and H to get g
其中A是Algorithm,D是Data,H是Hypothesis,g是goal
其总体的运行结构如图所示
![[台大机器学习笔记整理]perceptron learning algorithm_第1张图片](http://img.e-com-net.com/image/info8/735ba99d14b645a7b42ae0add9e5b57c.jpg)
接下来以最简单的感知器举例说明
感知器模型
最简单的二分线性感知器,由各维度乘以其权重,相加后,得到的结果与阈值进行比较,并得出结论。
用公式描述,则是如下:
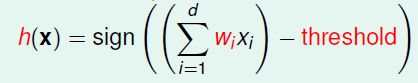
在这里我们将与阈值比较的这一过程直接放在了算式中,得到结果后判断结果与0的大小关系即可
将以上式子向量化,可以得到
h(x)=sign(w.T*x)
在这里,上面的式子即是Hypothesis,是我们用于模拟实际情况的一个假设模型。
感知器学习算法(Perceptron Learning Algorithm)
容易看到,一个假设一般有参数(如上面式子中的w)供我们进行调整,这样我们能根据Data对其进行调整,最后得到一个尽可能接近实际的映射(f)的一个映射关系g。
既然是machine learning,那么调整这一步当然是交给machine了。machine如何到达这一目的的方式,就是我们需要的learning algorithm。
用最简单的输入两个维度的perceptron(Hypothesis: h(x)=sign(w1x1+w2x2+w0))进行举例
![[台大机器学习笔记整理]perceptron learning algorithm_第2张图片](http://img.e-com-net.com/image/info8/6c962fcd860b477fbedc1bfa0b3b9d43.jpg)
如果令x1,x2为坐标轴,f(x)(即实际结果)以o或x的形式表现,那么我们需要的learning algorithm应该可以找到一条直线,像右图一样将两种结果分开,即一边为正,一边为负。右图中的分割直线可以认为f(x),即理想的映射关系。
![[台大机器学习笔记整理]perceptron learning algorithm_第3张图片](http://img.e-com-net.com/image/info8/a61f520e895149379563e940fed24236.jpg)
在这里,我们的修正方式是将原先的权重向量加上结果向量与维度向量的乘积。
当y=+1,那么类似于第一个图,w+yx将使得新的w更加偏向于x,以使得修正后的结果为h(x)>0,而类似有第二图的修正。
以算式进行说明,则是
(由correct的关系式可以推出)
理想情况下yw.T*x应该大于零,因此在需要进行correct的情况下(yw.T*x<0)并经过correct以后,yw.T*x比之前增加
Cyclic PLA:如此循环,直到跑了一圈(记录下最后一次出错的data的下标)后没有出现错误,则得到了我们的结果式子g
(当然,在这个算法中假设了所有数据是线性可分的,否则会陷入死循环)
这个即是在开头时所描述的我们令假设hypothesis接近于理想映射f所使用的learning algorithm,在运行完成后我们会得到一个形式类似假设hypothesis但w等参数均已经“学习”好了的映射关系g
(在PLA的运行过程中为了进行向量运算,会给x向量增加一个x0=1)
证明:在线性可分的前提下,PLA总是能够停下,得到最终将数据集中所有结果准确分开的一组w,作为goal

代入以下算式,得到
(对于每次update均能使当前的w更接近于理想的w)
第二个式子
![[台大机器学习笔记整理]perceptron learning algorithm_第5张图片](http://img.e-com-net.com/image/info8/823eb0e7ceaf4a5cb3a40d9297138f0a.jpg)
(w的模的增长是有限的)
第二个式子确保了wt不会增长过快
另外,由第一个式子的蓝色部分与第二个式子的红色部分(均令当前w的下标为T且一直推到w0=0时),最终可以得到
![[台大机器学习笔记整理]perceptron learning algorithm_第6张图片](http://img.e-com-net.com/image/info8/437576e232284cb2bad4a8b4c6f1c3d7.jpg)
左边即为理想的w与第T次修正后的w的内角cos值。因此,左边总是小于等于1
而后将左边置为1,可以得到T小于等于橙色式子中常数平方的倒数,因此通过有限的次数我们可以得到一个能成功将data按正确的结果切分开的w。
对Cyclic PLA的优化
以上对Cyclic PLA的介绍中可以明确看出其优缺点
有点:模型与算法简单,易于实现
缺点:仅适用于线性可分的数据,而且由于T与最终的理想w有关,其训练步数(在这里是correction)也是不确定的
首先考虑线性不可分的情况
理想状况下应该找到一个w,使得
![[台大机器学习笔记整理]perceptron learning algorithm_第7张图片](http://img.e-com-net.com/image/info8/a3a97f2e8730416daa129219d16628d3.jpg)
然而这是一个NP-hard问题,因此不考虑这一方式
因此采用pocket algorithm进行优化
pocket:保存当前得到的最理想的w,进行修正后如果得到的mistake数量更少,则更换为新的w
设置iteration的上限,在进行足够多次的循环后终止,并返回pocket中的w作为最终的结果
总结:
用perceptron learning algorithm为例子,介绍了机器学习的基本模型,即A takes D and H to get g
其中A是Algorithm,D是Data,H是Hypothesis,g是goal

通过A的学习逐步修正H中的w参数最终得到目标g
PLA的证明可以由correction的式子及假设一个最终的目标w通过一系列推导得到,在推导过程中还得到了性质(1)每次correct后w均会更接近于理想的w(2)w的模小于等于某个常数,这个常数与数据集有关
简单的Cyclic PLA存在(1)不适用于线性不可分问题(2)循环次数未知两个缺点,可以考虑使用pocket algorithm进行优化
import matplotlib.pyplot as plt
class perceptron:
def __init__(self,dimension):
#size=the dimension of x
self.dimension=dimension
self.w=np.zeros(dimension+1)
def cyclic_train(self,X,Y):
#X should be a list including the tuples storing the inputing x
w=self.w
train_set_size=len(X)
X=np.array([list(x)+[1] for x in X])
error_loc=range(train_set_size)
i=0
while i!=error_loc:
#correct and record the last error location
if sign(np.dot(X[i],w))!=Y[i]:
w=w+X[i]*Y[i]
error_loc=i
#move on and iterate cyclic
if i i+=1
else:
i=0
self.w=w
def predict(self,x):
return sign(np.dot(self.w,x))
def sign(x):
if x>0:
return 1
elif x<0:
return -1
else:
return 0
#The prepared test data
Xtr=[(2,4),(-1,2),(-3,-1),(-1,-4),(1,-1),(2,-4)]
Ytr=[1,1,1,-1,-1,-1]
#test
p1=perceptron(2)
p1.cyclic_train(Xtr,Ytr)
fig=plt.figure()
axes=fig.add_axes([0.1, 0.1, 0.8, 0.8])
axes.scatter([Xtr[i][0] for i in range(len(Xtr)) if Ytr[i]==1],\
[Xtr[i][1] for i in range(len(Xtr)) if Ytr[i]==1],color='red')
axes.scatter([Xtr[i][0] for i in range(len(Xtr)) if Ytr[i]==-1],\
[Xtr[i][1] for i in range(len(Xtr)) if Ytr[i]==-1],color='blue')
k=-p1.w[0]/p1.w[1]
b=-p1.w[2]/p1.w[1]
axes.plot([-10,10],[k*(-10)+b,k*10+b])
axes.spines['right'].set_color('none')
axes.spines['top'].set_color('none')
axes.xaxis.set_ticks_position('bottom')
axes.spines['bottom'].set_position(('data',0))
#set position of x spine to x=0
axes.yaxis.set_ticks_position('left')
axes.spines['left'].set_position(('data',0))
#set position of y spine to y=0
plt.show()
A takes D and H to get g
其中A是Algorithm,D是Data,H是Hypothesis,g是goal
其总体的运行结构如图所示
![[台大机器学习笔记整理]perceptron learning algorithm_第1张图片](http://img.e-com-net.com/image/info8/735ba99d14b645a7b42ae0add9e5b57c.jpg)
接下来以最简单的感知器举例说明
感知器模型
最简单的二分线性感知器,由各维度乘以其权重,相加后,得到的结果与阈值进行比较,并得出结论。
用公式描述,则是如下:
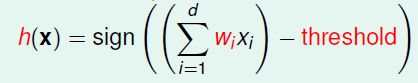
在这里我们将与阈值比较的这一过程直接放在了算式中,得到结果后判断结果与0的大小关系即可
将以上式子向量化,可以得到
h(x)=sign(w.T*x)
在这里,上面的式子即是Hypothesis,是我们用于模拟实际情况的一个假设模型。
感知器学习算法(Perceptron Learning Algorithm)
容易看到,一个假设一般有参数(如上面式子中的w)供我们进行调整,这样我们能根据Data对其进行调整,最后得到一个尽可能接近实际的映射(f)的一个映射关系g。
既然是machine learning,那么调整这一步当然是交给machine了。machine如何到达这一目的的方式,就是我们需要的learning algorithm。
用最简单的输入两个维度的perceptron(Hypothesis: h(x)=sign(w1x1+w2x2+w0))进行举例
![[台大机器学习笔记整理]perceptron learning algorithm_第2张图片](http://img.e-com-net.com/image/info8/6c962fcd860b477fbedc1bfa0b3b9d43.jpg)
如果令x1,x2为坐标轴,f(x)(即实际结果)以o或x的形式表现,那么我们需要的learning algorithm应该可以找到一条直线,像右图一样将两种结果分开,即一边为正,一边为负。右图中的分割直线可以认为f(x),即理想的映射关系。
如果我们需要得到一个近似于f的映射关系g,那么g首先应该能将我们手上的数据集中的数据准确的分开。
![[台大机器学习笔记整理]perceptron learning algorithm_第3张图片](http://img.e-com-net.com/image/info8/a61f520e895149379563e940fed24236.jpg)
在这里,我们的修正方式是将原先的权重向量加上结果向量与维度向量的乘积。
当y=+1,那么类似于第一个图,w+yx将使得新的w更加偏向于x,以使得修正后的结果为h(x)>0,而类似有第二图的修正。
以算式进行说明,则是
(由correct的关系式可以推出)
理想情况下yw.T*x应该大于零,因此在需要进行correct的情况下(yw.T*x<0)并经过correct以后,yw.T*x比之前增加
Cyclic PLA:如此循环,直到跑了一圈(记录下最后一次出错的data的下标)后没有出现错误,则得到了我们的结果式子g
(当然,在这个算法中假设了所有数据是线性可分的,否则会陷入死循环)
这个即是在开头时所描述的我们令假设hypothesis接近于理想映射f所使用的learning algorithm,在运行完成后我们会得到一个形式类似假设hypothesis但w等参数均已经“学习”好了的映射关系g
(在PLA的运行过程中为了进行向量运算,会给x向量增加一个x0=1)
证明:在线性可分的前提下,PLA总是能够停下,得到最终将数据集中所有结果准确分开的一组w,作为goal
线性可分,因此存在一组w令对所有y与x均有

则yw.T*x>0对于所有点均成立
代入以下算式,得到
(对于每次update均能使当前的w更接近于理想的w)
第二个式子
![[台大机器学习笔记整理]perceptron learning algorithm_第5张图片](http://img.e-com-net.com/image/info8/823eb0e7ceaf4a5cb3a40d9297138f0a.jpg)
(w的模的增长是有限的)
第二个式子确保了wt不会增长过快
另外,由第一个式子的蓝色部分与第二个式子的红色部分(均令当前w的下标为T且一直推到w0=0时),最终可以得到
![[台大机器学习笔记整理]perceptron learning algorithm_第6张图片](http://img.e-com-net.com/image/info8/437576e232284cb2bad4a8b4c6f1c3d7.jpg)
左边即为理想的w与第T次修正后的w的内角cos值。因此,左边总是小于等于1
而后将左边置为1,可以得到T小于等于橙色式子中常数平方的倒数,因此通过有限的次数我们可以得到一个能成功将data按正确的结果切分开的w。
对Cyclic PLA的优化
以上对Cyclic PLA的介绍中可以明确看出其优缺点
有点:模型与算法简单,易于实现
缺点:仅适用于线性可分的数据,而且由于T与最终的理想w有关,其训练步数(在这里是correction)也是不确定的
首先考虑线性不可分的情况
理想状况下应该找到一个w,使得
![[台大机器学习笔记整理]perceptron learning algorithm_第7张图片](http://img.e-com-net.com/image/info8/a3a97f2e8730416daa129219d16628d3.jpg)
然而这是一个NP-hard问题,因此不考虑这一方式
因此采用pocket algorithm进行优化
pocket:保存当前得到的最理想的w,进行修正后如果得到的mistake数量更少,则更换为新的w
设置iteration的上限,在进行足够多次的循环后终止,并返回pocket中的w作为最终的结果
总结:
用perceptron learning algorithm为例子,介绍了机器学习的基本模型,即A takes D and H to get g
其中A是Algorithm,D是Data,H是Hypothesis,g是goal
在PLA中,A即为perceptron learning algorithm(precisely, Cyclic PLA),Hypothesis是线性模型

通过A的学习逐步修正H中的w参数最终得到目标g
PLA的证明可以由correction的式子及假设一个最终的目标w通过一系列推导得到,在推导过程中还得到了性质(1)每次correct后w均会更接近于理想的w(2)w的模小于等于某个常数,这个常数与数据集有关
简单的Cyclic PLA存在(1)不适用于线性不可分问题(2)循环次数未知两个缺点,可以考虑使用pocket algorithm进行优化
附录:
python的简单pla实现
import matplotlib.pyplot as plt
class perceptron:
def __init__(self,dimension):
#size=the dimension of x
self.dimension=dimension
self.w=np.zeros(dimension+1)
def cyclic_train(self,X,Y):
#X should be a list including the tuples storing the inputing x
w=self.w
train_set_size=len(X)
X=np.array([list(x)+[1] for x in X])
error_loc=range(train_set_size)
i=0
while i!=error_loc:
#correct and record the last error location
if sign(np.dot(X[i],w))!=Y[i]:
w=w+X[i]*Y[i]
error_loc=i
#move on and iterate cyclic
if i
else:
i=0
self.w=w
def predict(self,x):
return sign(np.dot(self.w,x))
def sign(x):
if x>0:
return 1
elif x<0:
return -1
else:
return 0
#The prepared test data
Xtr=[(2,4),(-1,2),(-3,-1),(-1,-4),(1,-1),(2,-4)]
Ytr=[1,1,1,-1,-1,-1]
#test
p1=perceptron(2)
p1.cyclic_train(Xtr,Ytr)
fig=plt.figure()
axes=fig.add_axes([0.1, 0.1, 0.8, 0.8])
axes.scatter([Xtr[i][0] for i in range(len(Xtr)) if Ytr[i]==1],\
[Xtr[i][1] for i in range(len(Xtr)) if Ytr[i]==1],color='red')
axes.scatter([Xtr[i][0] for i in range(len(Xtr)) if Ytr[i]==-1],\
[Xtr[i][1] for i in range(len(Xtr)) if Ytr[i]==-1],color='blue')
k=-p1.w[0]/p1.w[1]
b=-p1.w[2]/p1.w[1]
axes.plot([-10,10],[k*(-10)+b,k*10+b])
axes.spines['right'].set_color('none')
axes.spines['top'].set_color('none')
axes.xaxis.set_ticks_position('bottom')
axes.spines['bottom'].set_position(('data',0))
#set position of x spine to x=0
axes.yaxis.set_ticks_position('left')
axes.spines['left'].set_position(('data',0))
#set position of y spine to y=0
plt.show()
![[台大机器学习笔记整理]perceptron learning algorithm_第4张图片](http://img.e-com-net.com/image/info8/6a4e6e8f03924e8abfca5adefb012d8f.jpg)