线性回归、梯度下降算法与 tensorflow
举个栗子
考虑一个二手房交易记录数据集. 已知房屋面积,卧室数量和交易价格:
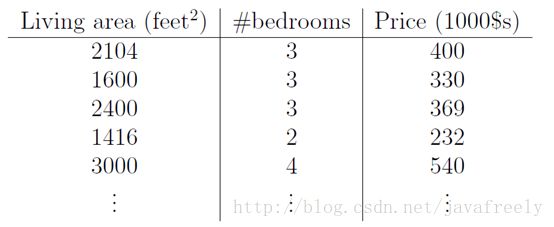
根据这个数据集,要求我们估算当前某个给定房屋价格. 我们应该怎么做?
线性回归
回归就是根据已知数据来预测另一个数值型数据的目标值. 假设特征和结果满足线性关系:
h(x)=w0+w1x1+w2x2
其中 w 为权重. 假设 x0 为1, 则上面公式也可以写作:
h(x)=∑i=0nwixi=wTx
其中 n 为参数个数. 现在模型的形式已经有了,剩下的就是根据已有数据计算出一个合适的 w.
损失函数
什么样的参数 w 才算是合适的呢? 直观上看,如果有一组 w,使得在 训练集上预测值和实际值之间的差异最小,则 w 就是最合适的. 我们选择了差值的平方和作为衡量标准. 为了便于计算前面加常量 1/2.
J(w)=12∑i=1m(hw(x(i))−y(i))2
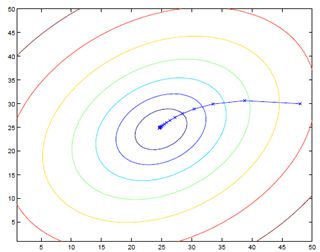
梯度下降
损失函数 J(w) 是w 的函数,现在需要求使其达到最小值时的 w.
在一元函数 f(x) 求最小值问题中,我们可以从某个初始值 x0 开始,求 f′(x0) , 然后向下降方向移动一段距离(走一步)得到 x1=x0−f′(x0) ,这样一步一步走下去,就会距离目标值越来越近.
梯度同导数,只不过是在多维空间的导数. w 的更新可以用梯度下降来进行:
w=w−α∇wJ(w)
梯度下降算法整体表示如下:
Repeat until convergence {
w=w−α∇wJ(w)
}
tensorflow 实现线性回归
我们用 tensorflow 实现了线性回归. 这里需要注意,我们使用了 AdamOptimizer,而不是标准的 GradientDescentOptimizer. AdamOptimizer 对梯度下降进行了部分优化. 在我们的例子里,如果直接使用 GradientDescentOptimizer 返回的结果会得到 ‘nan’. 因此使用 AdamOptimizer 执行梯度下降.
import tensorflow as tf
W = tf.Variable(tf.ones([2,1]), tf.float32)
b = tf.Variable([5.0], tf.float32)
x = tf.placeholder(tf.float32, [None, 2])
y = tf.placeholder(tf.float32)
y_ = tf.matmul(x, W) + b
loss = tf.reduce_sum(tf.square(y_ - y))
#optimizer = tf.train.GradientDescentOptimizer(0.01)
#optimizer = tf.train.AdagradOptimizer(0.01)
optimizer = tf.train.AdamOptimizer(0.01)
train = optimizer.minimize(loss)
x_train = [
[2104, 3],
[1600, 3],
[2400,3],
[1416,2],
[3000,4]
]
y_train = [400,330,369,232,540]
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(40000):
curr_W, curr_b, _ = sess.run([W, b, train], {x:x_train, y:y_train})
curr_W, curr_b, curr_loss = sess.run([W, b, loss], {x:x_train, y:y_train})
print("W: %s b: %s loss: %s" % (curr_W, curr_b, curr_loss))