《深度学习入门——基于python的理论与实现》读书笔记（五）

数值微分的速度太慢

上一章我们用数值微分的方法计算梯度，每计算一个点（参数矩阵中的一个元素，即一个参数），我们都要万郴两次预测操作（算出一前一后两个微小变化处的函数值），再做两次算术运算（两个函数值做差，再除以2 * h）——这太慢了。

利用知识降低复杂度

降低复杂度的撒手锏是知识。如果能发现问题内在的数学规律，也就是比较深刻地理解问题，则可以极大地降低计算复杂度。我们的数值微分方法是直接依照导数的定义式编写的，没有利用具体函数的信息。如果结合具体函数，就可以利用微积分知识得到导函数，即斜率关于输入（或输出）的函数。在这个问题中，得到梯度的解析解之后，求梯度的速度可以大大加快。

反向传播的动因

我们的想法是，利用解析解为求解提速。神经网络的损失是输入和网络参数的函数，取一批训练样本作为输入，把参数视为变量，可以对它们求导。损失函数再复杂（神经网络层数越多，损失函数越复杂）也是若干仿射变换、激活函数以及softmax的叠加。利用链式法则，我们总能把导函数求出来。但是经实践发现，这样直接求解（试图把导数用各个参数表示出来）至少有两方面缺陷：

• 求解过程费时费力，并且随着神经网络加深变得越发艰难
• 不同的网络有不一样的导数，每次创建新网络都要计算一次导函数，不能一劳永逸地解决问题

怎么克服这个困难呢，有没有一劳永逸的办法？

我们的思路是，根据链式法则，一个量A关于另一个量W的导数与W是怎么计算出来的无关，又由于神经网络同一层的神经元执行相同的运算（因此具有相同形式的局部导数（这一层的输出关于这一层的输入（也许这是上一层的输出）的导数）），我们可以让层记忆与求局部导数相关的计算（做预测）的中间结果，再从后往前（从输出向输入）逐层逐中间变量计算导数，最终得到损失关于输入的导数。

计算图，表达式树

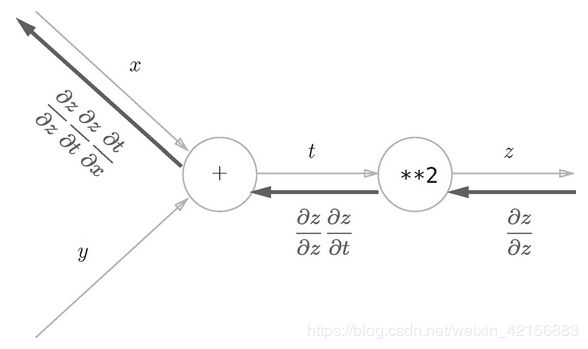
利用计算图可以直观地理解反向传播，

上面的计算图表达算式( :=, 这是python内建幂运算语法)：

如图，对的导数是对自身的导数（是1，因为自己变化引起的自身变化是等同的）乘以对的导数，对的导数要再乘上对的导数（这和连接与的是加法运算有关，详见下文）。其中每一个导数值，要么是上面传播下来的，要么可以通过之前保存的中间运算结果算出。

反向传播的实现

各层

class ReLU:
    def __init__(self):
        self.mask = None
        
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        return out
    
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

class sigmoid:
    def __init__(self):
        self.out = None
    
    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        return dx

仿射变换层（矩阵乘法计算层），

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None
    
    def forward(self, x):
        self.x = x
        out = x @ self.W + self.b
        return out
    
    def backward(self, dout):
        dx = dout @ self.W.T
        self.dW = self.x.T @ dout
        self.db = np.sum(dout, axis=0)
        return dx

最后一层，和loss结合在一起，

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None # 损失
        self.y = None    # softmax的输出
        self.t = None    # 监督数据（one-hot vector)
    
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss
    
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        return dx

两层网络类

class TwoLayerNet:
    
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)
        
        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
        
        self.lastLayer = SoftmaxWithLoss()
    
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x) # 层层递进
        return x
    
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1:
            t = np.argmax(t, axis=1)
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
    
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        return grads
    
    def gradient(self, x, t):
        # forward
        self.loss(x, t)
        
        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)
        
        # 设定
        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db
        
        return grads

可见，将各层像拼积木一样组合起来。

训练部分的代码不新鲜，

for i in range(iter_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 通过误差反向传播求梯度
    grad = network.gradient(x_batch, t_batch)
    
    # 更新
    for key in network.params:
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)

小结

从计算图中获得灵感，让梯度逐层计算，反向传播，真是巧妙的想法！