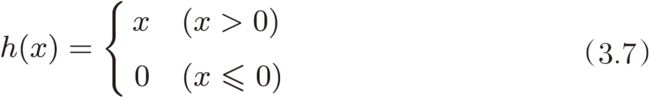gitchat训练营15天共度深度学习入门课程笔记(三)

3.1　神经网络

之前的学习通过真值表、赋值计算、公式运算、单层感知机（已经可以确定其中的参数权重）叠加等方法来实现了感知机的表示，但是都是低效率的人工工作。
此时，神经网络的出现就很好的解决了这个问题，它可以自己从一堆给定的数据中寻找适合的参数权重。

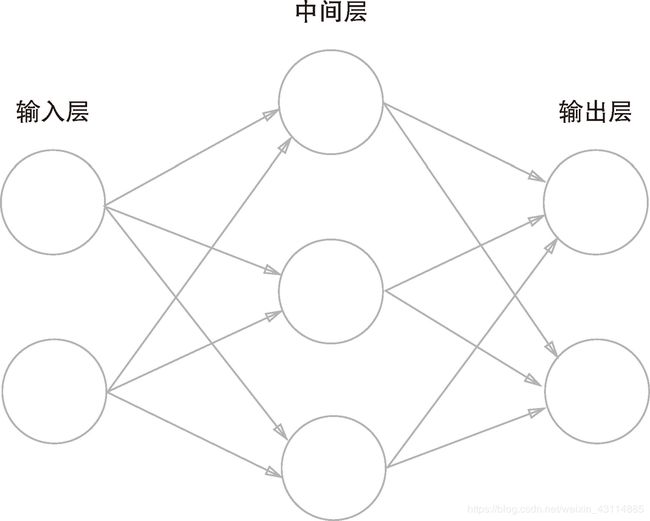
3.1.1　神经网络的例子

• 最左面的一列神经元作为输入层，最右面的一列神经元作为输出层，中间的所有列作为中间层/隐藏层
• 为了方便python实现，最左面从0层开始递增。
• 注意本书中按照神经元具有的权重的数量来定义：2层神经网络
• 根据上一章的内容，我们可以看到2层感知机和2层神经网络表示的结构是很相似的
• 感知机和神经网络区别如下：

1. 感知机只有一个输出，只有两层神经网络构成
2. “朴素感知机”激活函数为阶跃函数（输入超过阀值theta，切换输出函数），神经网络的激活函数是平滑的函数，而且所有神经网络的激活函数都必须是非线性的，当感知机的激活函数改变，可以成为神经网络。
3. 感知机不能解决非线性不可分问题，但是神经网络和多层感知机可以解决
4. 有时候多层感知机就是神经网络

3.1.2　复习感知机

我们知道上一章学习的带偏置的感知机的分段函数式如下，同时将偏置的权值置为1是可以得到如下图的神经网络


当我们把偏置和输入的总和用一个a来代替是，就替换出了一个更简洁的函数表示方法:y=h(a),a=b+w1x1+w2x2,可以得出的值如下：

• 上式在输入小于等于0时输出为0，在大于0时输出为1

3.1.3　激活函数

激活函数：将输入信号总和转化为输出信号的函数（类似上面的h(x)）,另一种说法，用来激活输入信号
表示图像如下：

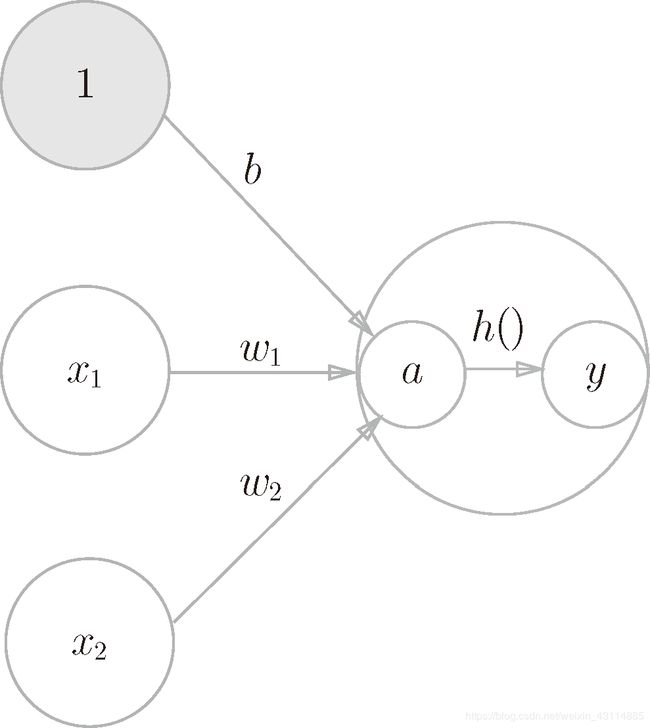
• 上图中的○表示了激活函数计算过程
• 神经元中的○成为一个节点，图中激活函数将节点a转换成了节点y，节点性质与神经元相同

3.2　激活函数

3.2.1　sigmoid 函数

sigmoid 函数（sigmoid function）公式如下：

• $h(n)=\frac{1}{1+{\mathrm{e}}^{-x}}$

3.2.2　阶跃函数的实现

1. 简单实现

def step_function(x):
    if x<=0:
        return 0
    elif x>0:
        return 1

2.运用Numpy数组

def step_function(x):
    y = x > 0
    return y.astype(np.int)

python解释器：

>>> import numpy as np
>>> x=np.array([-1.0,2.0,1.0])
>>> y=x>0
>>> y
array([False,  True,  True])
>>> y.dtype
dtype('bool')
>>> y=y.astype(np.int)  #将bool类型的数组转化为int类型
>>> y
array([0, 1, 1])
>>> y.dtype
dtype('int64')

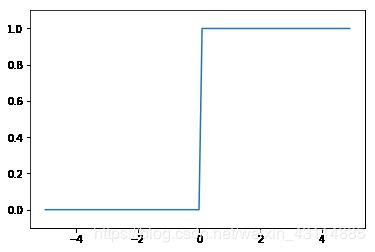
3.2.3　阶跃函数的图形

%matplotlib inline
import numpy as np
import matplotlib.pylab as plt

def step_function(x):
    return np.array(x>0,dtype=int)

x=np.arange(-5.0,5.0,0.1) #在-5.0到5.0范围内以0.1作为单位生成numpy数组
y = step_function(x) #对数组各个元素进行阶跃函数计算
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

运行结果如下：

• 得到的输出只有0，1，中间的过程是像阶梯一样的，所以叫阶跃函数。

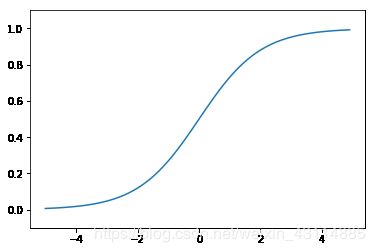
3.2.4　sigmoid 函数的实现

根据前面所给出的公式写下函数即可：

def sigmoid(x):
    return 1/(1+np.exp(-x))

• 由于numpy的广播性，可以在此处输入，并且会自动广播，每个元素都会进行计算。而之前的简单实现阶跃函数，由于是按每个元素单一输出来进行函数的返回的，没有广播的功能，所以不能用numpy。

图形绘制如下：

%matplotlib inline
import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    return 1/(1+np.exp(-x))

x=np.arange(-5.0,5.0,0.1) #在-5.0到5.0范围内以0.1作为单位生成numpy数组
y =sigmoid(x) #对数组各个元素进行sigmoid函数计算
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

运行结果如下：

3.2.5　sigmoid 函数和阶跃函数的比较

我们把sigmoid函数和阶跃函数一起比较：

%matplotlib inline
import numpy as np
import matplotlib.pylab as plt

def step_function(x):
    return np.array(x>0,dtype=int)
def sigmoid(x):
    return 1/(1+np.exp(-x))

x=np.arange(-5.0,5.0,0.1) 
y = step_function(x)
z=sigmoid(x)
plt.plot(x, y,linestyle="--",label="step_function") #以虚线表示阶跃函数
plt.plot(x,z,label="sigmoid") #以实线来表示sigmoid函数
plt.ylim(-0.1, 1.1) 
plt.legend()#将标签显示出来
plt.show()

相同点：

• 输出信号在0、1之间
• 输入信号重要性低，输出信号趋向于1；输入信号重要性高，输出信号趋向于1
• 都是非线性函数

不同点：

• 平滑性
• 阶跃函数输出信号只有0、1，而sigmoid函数可以有不同的输出信号

3.2.6　非线性函数

神经网络的激活函数必须使用非线性函数
原因：当使用线性函数时，没有了隐藏层，叠加层数是没有意义的。
如使用y=h(a),a=cx时叠加多层为y=h(h(h(a))),a=cx，可以直接用$y=c^{3}x$ 来表示，即多次乘法即可得到

3.2.7　ReLU 函数

函数式如下：

实现如下：

%matplotlib inline
import numpy as np
import matplotlib.pylab as plt

def relu(x):
    return np.maximum(0, x)  #调用maximun选择0，x中的大者

x=np.arange(-6.0,6.0,0.1) 
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.0) 
plt.show()

运行结果如下：

3.3　多维数组的运算

3.3.1　多维数组

• 一维数组

>>> import numpy as np
>>> x=np.array([1,2,3,4])
>>> x
array([1, 2, 3, 4])
>>> x.ndim #显示x的维数，以int结果返回
1
>>> x.shape #显示x的形状，每一维如何构成
(4,)
>>> x.shape[0] #显示第一维的形状
4

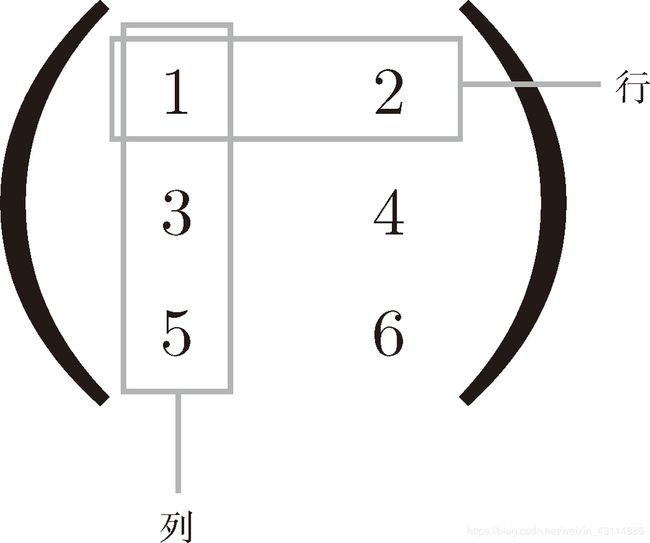
• 二维数组（矩阵）

>>> B = np.array([[1,2], [3,4], [5,6]])
>>> print(B)
[[1 2]
 [3 4]
 [5 6]]
>>> np.ndim(B)
2
>>> B.shape
(3, 2)

矩阵形状如下：

3.3.2　矩阵乘法

• 结果矩阵R的第n行第m列元素是$\mathbf{A}$的第n列和$\mathbf{B}$的第m列相乘又相加结果
• 矩阵$\mathbf{A}$ 的第 1 维的元素个数（列数）必须和矩阵 $\mathbf{B}$ 的第 0 维的元素个数（行数）相等
• 在看数组的维度和对应矩阵的维度时，矩阵的维度从0维开始算起
• $\mathbf{A}$、$\mathbf{B}$顺序不同得到R也不同
• 另外，在本书的数学标记中，矩阵将用黑斜体表示（比如，矩阵 $\mathbf{A}$），以区别于单个元素的标量（比如，a 或 b）
  实现如下：

>>> A=np.array([[1.0,3.0],[2.0,5.0],[4.0,2.0]])
>>> B=np.array([[3.0,2.0],[1.0,4.0]])
>>> R=np.dot(A,B) #np.dot()函数计算乘积
>>> R
array([[ 6., 14.],
       [11., 24.],
       [14., 16.]])

• A的列维度和B的行维度不同的结果：

>>> C = np.array([[1,2], [3,4]])
>>> C.shape
(2, 2)
>>> A.shape
(2, 3)
>>> np.dot(A, C)
Traceback (most recent call last):
  File "", line 1, in <module>
ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)

3.3.3　神经网络的内积

下面我们使用 NumPy 矩阵来实现神经网络。这里我们以图中的简单神经网络为对象。这个神经网络省略了偏置和激活函数，只有权重。

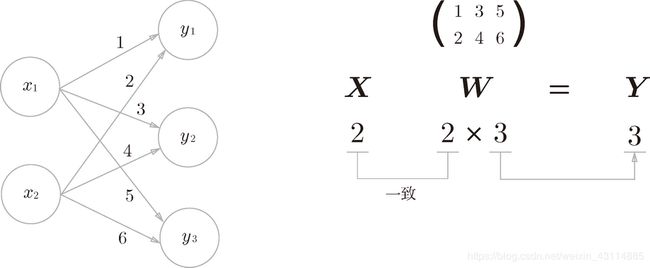
>>> x=np.array([1,2,3])
>>> w=np.array([[2,5,1],[3,2,1],[1,1,2]])
>>> w.ndim
2
>>> w.shape
(3, 3)
>>> x.shape
(3,)
>>> y=np.dot(x,w)
>>> y
array([11, 12,  9])

end

• 原书为《深度学习入门 基于Python的理论与实现》作者：斋藤康毅
  人民邮电出版社
• 本文章是gitchat的《陆宇杰的训练营：15天共读深度学习》¹的课程读书笔记
• 本文章大量引用原书中的内容和训练营课程中的内容作为笔记

---

1. 《陆宇杰的训练营：15天共读深度学习》 ↩︎