最短路径问题
1.只有5行的Floyd-Warshall算法
#include
int main()
{
int e[10][10], k, i, j, n, m, t1, t2, t3;
int inf = 99999999;
scanf("%d %d",&n, &m);
for(i = 1; i <= n; i++)
for(j = 1; j <= n; j++)
if(i == j) e[i][j] = 0;
else e[i][j] = inf;
for(i = 1; i <= m; i++)
{
scanf("%d %d %d", &t1, &t2, &t3);
e[t1][t2] = t3;
}
/* 核心代码 */
/* 思想:从只允许经过1号顶点进行中转, 接下来只允许经过1,2顶点中转...,然后可以经过所有顶点中转,求两点之间的最短路径 */
for(k = 1; k <= n; k++)
for(i = 1; i <= n; i++)
for(j = 1; j <= n; j++)
if(e[i][j] > e[i][k]+e[k][j])
e[i][j] = e[i][k] + e[k][j];
for(i = 1; i <= n; i++)
{
for(j = 1; j <= n; j++)
{
printf("%-10d", e[i][j]);
}
printf("\n");
}
return 0;
}
/* in */
/*
4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12*/
/* out */
/*
0 2 5 4
9 0 3 4
6 8 0 1
5 7 10 0 */ 2.单源最短路径--Dijkstra算法
邻接矩阵法:
原作者的链接:http://blog.51cto.com/ahalei/1387799
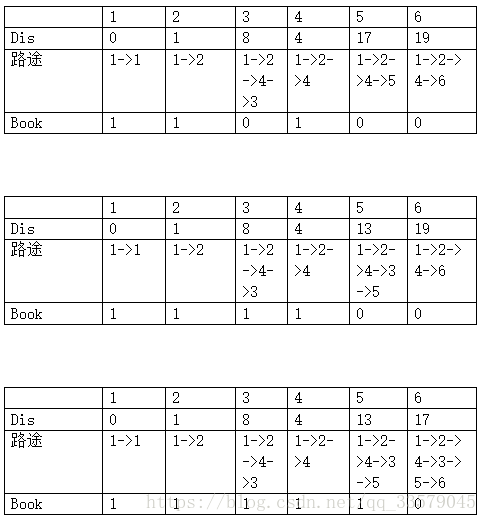
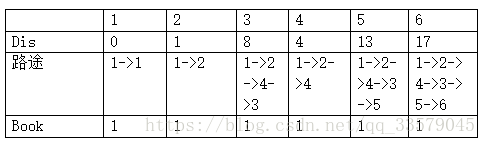
Dijkstra为“单源最短路径算法”
#include
int main()
{
// e为邻接矩阵, dis为源点到各个顶点的初始路程, book为标记数组
int e[15][15], dis[15], book[15], i, j, n, m, t1, t2, t3, u, v, min;
int inf = 999999;
scanf("%d %d", &n, &m);
for(i = 1; i <= n; i++)
for(j = 1; j <= n; j++)
if(i == j) e[i][j] = 0;
else e[i][j] = inf;
for(i = 1; i <= m; i++)
{
scanf("%d %d %d", &t1, &t2, &t3);
e[t1][t2] = t3;
}
for(i = 1; i <= n; i++){
dis[i] = e[1][i];
book[i] = 0;
}
// 默认1为源点
book[1] = 1;
/* Dijkstra 核心算法 */
for(i = 1; i <= n-1; i++)
{
min = inf;
for(j = 1; j <= n; j++)
{
if(book[j] == 0 && dis[j] < min)
{
min = dis[j];
u = j;
}
}
book[u] = 1;
for(v = 1; v <= n; v++)
{
if(e[u][v] < inf)
{
if(dis[v] > e[u][v]+dis[u])
dis[v] = e[u][v]+dis[u];
}
}
}
for(i = 1; i <= n; i++)
printf("%d ", dis[i]);
return 0;
}
/* in */
/*
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4 */
/* out */
/*
0 1 8 4 13 17 */ 邻接表法:
图片来自:https://blog.csdn.net/wr_technology/article/details/51025252
这里用u、v和w三个数组用来记录每条边的具体信息,数组下标即为读入边的次序,u[i]、v[i]、w[i]表示第i条边是从第u[i]号顶点到v[i]号顶点(u[i]->v[i])
first数组的第1-n个单元分别存储1-n号顶点第一条边的编号(其实是这个顶点最后读入的边的编号,结合代码自行体会),初始没有入边, 初始化为-1。
即first[u[i]]保存顶点u[i]的第一条边的编号, next[i]存储编号为i的边的下一条边的编号。
关于读入边的过程我想拿出来具体说一下, 感觉自己理解复杂了:
for(i = 1; i <= n; i++)
first[i] = -1;
for(i = 1; i <= m; i++)
{
scanf("%d %d %d", &u[i], &v[i], &w[i]);
next[i] = first[u[i]]; /* 1 */
first[u[i]] = i; /* 2 */
}point 1 : 这个比较难解释,我也不知道自己有没有理解复杂了。。,在每一次更新first数组前,都会让next记录顶点为u[i]最后出现的编号(这里的编号是指边出现的顺序)。为甚么通过next和first能够记录以u[i]为顶点的所有边呢,就是这一延迟记录的特性:以上面的图为例,当next[3]=1时,在编号为3时又出现了顶点1,此时next的这个下标3就是最新发现的顶点为1的编号,而next[3]的值,则指向了上一次出现顶点1的编号,大概就是这么个道理------,有点乱
point 2: 等next更新完了,我们在记录顶点u[i]的编号,可以知道,这个编号是顶点u[i]到目前为止最后出现的一次,同时这个i在next数组中如果作为下标的话,就是顶点u[i]倒数第二条边出现的编号
或者这样说(刷牙时又想了一下)?
就是如果与一个顶点相关的边还没有被读到,那么next[i]中在没有遇到与这个顶点相关的第二条边时不会记录与这个顶点相关的信息,而是记录在first数组中。直到第二次遇到这个顶点,next数组会在fisrt数组中读取上一次这个顶点出现的编号(uvw中的下标),并且用这次出现的编号作为其下标,这样就可以通过first和next找到有关一个顶点的所有边了。
此时,如果我们想遍历1号顶点的每一条边就很简单了。1号顶点的其中一条边的编号存储在first[1]中。其余的边则可以通过next数组寻找到。请看下图。
#include
int dis[7], inf = 99999999, flag[7], u[10], v[10], w[10];
int first[7], next[10];
int main()
{
int n, m, i, j, l;
scanf("%d %d", &n, &m);
for(i = 1; i <= n; i++)
first[i] = -1;
for(i = 1; i <= m; i++)
{
scanf("%d %d %d", &u[i], &v[i], &w[i]);
next[i] = first[u[i]]; /* 这个比较难解释,我也不知道自己有没有理解复杂了。。,在每一次更新first数组前,都会让next记录顶点为u[i]最后出现的编号(这里的编号是指边出现的顺序)。为甚么通过next和first能够记录以u[i]为顶点的所有边呢,就是这一延迟记录的特性:以上面的图为例,当next[3]=1时,在编号为3时又出现了顶点1,此时next的这个下标3就是最新发现的顶点为1的编号,而next[3]的值,则指向了上一次出现顶点1的编号,大概就是这么个道理------,有点乱 */
first[u[i]] = i; /* 等next更新完了,我们在记录顶点u[i]的编号,可以知道,这个编号是顶点u[i]到目前为止最后出现的一次,同时这个i在next数组中如果作为下标的话,就是顶点u[i]倒数第二条边出现的编号 */
}
for(i = 1; i <= n; i++)
dis[i] = inf;
int k = first[1]; // 得到顶点1最后一条边的编号
while(k != -1)
{
dis[v[k]] = w[k];
k = next[k];
}
dis[1] = 0;
flag[1] = 1;
for(i = 1; i <= n-1; i++)
{
int min = inf;
for(j = 1; j <= n; j++)
{
if(flag[j] == 0 && dis[j] < min)
{
min = dis[j];
l = j;
}
}
flag[l] = 1;
int k = first[l]; // 中转点l, 获得其编号
while(k != -1) /*找到和这个中转点所有相关的边,看从1出发,经过这个中转点能否使得路途变短*/
{
if(dis[l] + w[k] < dis[v[k]])
{
dis[v[k]] = dis[l] + w[k];;
}
k = next[k];
}
}
for(i = 1; i <= n; i++)
printf("%d ", dis[i]);
return 0;
} 3.明天来搞Bellman-Ford算法,今晚先预热下