生成对抗网络的tensorflow实现
生成对抗网络的tensorflow实现
原文地址:http://blog.evjang.com/2016/06/generative-adversarial-nets-in.html
这是关于使用tensorflow来实现Goodfellow的生成对抗网络论文的教程。对抗网络是一个可以使用大约80行的python代码就可以实现的一个有趣的小深度学习练习,这将使你进入深度学习的一个活跃领域:生成式模型。
Github上的源码
情景:假币
为了更好地解释这篇论文的动机,这里提供一个假设场景:
Danielle是一个银行的出纳员,她的工作职责之一就是辨别真币与假币。George是一个制造假币的骗子,因为免费的钱相当激进。
让我们简化一下:假定货币的唯一显著特征就是印在每个钞票上的唯一编号 X 。这些编码是一个概率分布的随机抽样,其中密度函数 pdata 只有国家财政部知道(这意味着Danielle与George都不知道)。方便起见,这个教程使用 pdata 同时指代这个分布与它的概率密度函数(尽管从本质上说概率分布与它的密度函数并不相同)。
George的目标是从 pdata 生成样例 x′ ,所以他制造的假币与真币难以区分。你可能会问:George事先并不知道 pdata ,他怎么能从 pdata 采样?
我们可以在不知道真实的潜在生成过程的情况下制造出计算不可区分的样例[1]。这个潜在的生成过程是财政部所使用的生成样例 X 的方法-也许是从 pdata 抽样的一些有效算法,这些算法依赖于概率密度分布的解析式。
我们可以将这种算法看做“自然(函数)基”,财政部将使用这种直接的方法来印制我们假设的钞票。然而,一个(连续)函数可以用一系列不同的基函数来表征;George 可以使用“神经网络基”,“傅里叶基”或者其它的能用来构建近似器的基来表示相同的抽样算法。从局外人的角度来看,这些抽样器是计算上不可区分的,然而 George的模型并没有将 pdata 的自然抽样基或者解析式泄露给他。
背景:判别模型 vs 生成模型
我们使用 X 和 Y 代表“观测”和“目标”随机变量。 X 和 Y 的联合分布为 P(X,Y) ,我们可以将其看做两变量(可能相关)的概率密度函数。
一个判别式模型可以用来评估条件概率 P(Y|X) 。例如,给定一个代表像素点的向量 x ,那么 Y=6 的概率是多少?(6代表是虎斑猫的类别标签)。 MNIST LeNet, AlexNet和其他的分类器都是判别式模型的实例。
另外一方面,一个生成式模型可以用来估计联合分布 P(X,Y) 。这意味着我们可以选取 (X,Y) 值对,然后使用舍取抽样法来从 P(X,Y) 来获得样例 x,y 。使用正确的生成模型的另外一种方式,我们可以将一些分布在 [0,1] 上的随机值转化为一个兔子图。这会很有趣。
当然,生成模型比判别模型更难构建,这两者都是统计学与机器学习研究的热点领域。
生成对抗网络
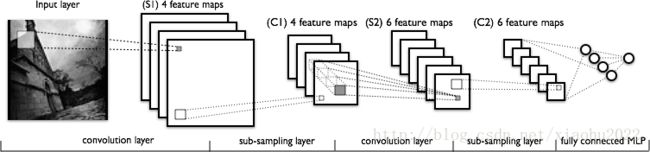
Goodfellow的论文提出了一个优雅的方式来将神经网络训练成一个可以表示任何(连续)概率密度函数的生成模型。我们构建两个神经网络,分别是 D (Danielle)和 G (George),然后使用它们来玩一个对抗式的猫捉老鼠的游戏: G 是一个生成器,它尝试着从 pdata 生成伪样例;而 D 是一个决策器,它试着不会被骗。我们同时训练它们,所以它们将在相互抗争中互相得到提高。当收敛时,我们希望 G 能够学会完全从 pdata 抽样,此时 D(x)=0.5 (随机猜测)。
对抗网络已经成功地用来凭空合成下列类型的图片:
在这个教程里,我们不会做任何很神奇的东西,但是希望你将会对对抗网络有一个更基本的了解。
实现
我们将训练一个神经网络用来从简单的一维正态分布 N(−1,1) 中抽样。
这里 D,G 都是小的3层感知机,每层总共有稀薄的11个隐含单元。 G 的输入是一个噪音分布 z∼uniform(0,1) 中的单个样例。我们想使用 G 来将点 z1,z2,...zM 映射为 x1,x2,...xM ,这样映射的点 xi=G(zi) 在 pdata(X) 密集的地方会密集聚集。因此,在 G 中输入 z 将生成伪数据 x′ 。
同时,判别器 D ,以 x 为输入,然后输出该输入属于 pdata 的可能性。令 D1 和 D2 为 D 的副本(它们共享参数,那么 D1(x)=D2(x) )。 D1 的输入是从合法的数据分布 x∼pdata 中得到的单个样例,所以当优化判别器时我们想使 D1(x) 最大化。 D2 以 x′ ( G 生成的伪数据)为输入,所以当优化 D 时,我们想使 D2(x) 最小化。 D 的价值函数为:
这里是Python代码:
batch = tf.Variable(0)
obj_d = tf.reduce_mean(tf.log(D1)+tf.log(1-D2))
opt_d = tf.train.GradientDescentOptimizer(0.01)
.minimize(1-obj_d,global_step=batch,var_list=theta_d)我们之所以要不厌其烦地指定 D 的两个副本 D1 和 D2 ,是因为在tensorflow中,我们需要 D 的一个副本以 x 为输入,而另外一个副本以 G(z) 为输入;计算图的相同部分不能被重用于不同的输入。
当优化 G 时,我们想使 D2(X′) 最大化(成功骗过 D )。 G 的价值函数为:
batch=tf.Variable(0)
obj_g=tf.reduce_mean(tf.log(D2))
opt_g=tf.train.GradientDescentOptimizer(0.01)
.minimize(1-obj_g,global_step=batch,var_list=theta_g)在优化时我们不是仅在某一刻输入一个值对 (x,z) ,而是同时计算 M 个不同的值对 (x,z) 的损失梯度,然后用其平均值来更新梯度。从一个小批量样本中估计的随机梯度与整个训练样本的真实梯度非常接近。
训练的循环过程是非常简单的:
# Algorithm 1, GoodFellow et al. 2014
for i in range(TRAIN_ITERS):
x= np.random.normal(mu,sigma,M) # sample minibatch from p_data
z= np.random.random(M) # sample minibatch from noise prior
sess.run(opt_d, {x_node: x, z_node: z}) # update discriminator D
z= np.random.random(M) # sample noise prior
sess.run(opt_g, {z_node: z}) # update generator G流形对齐
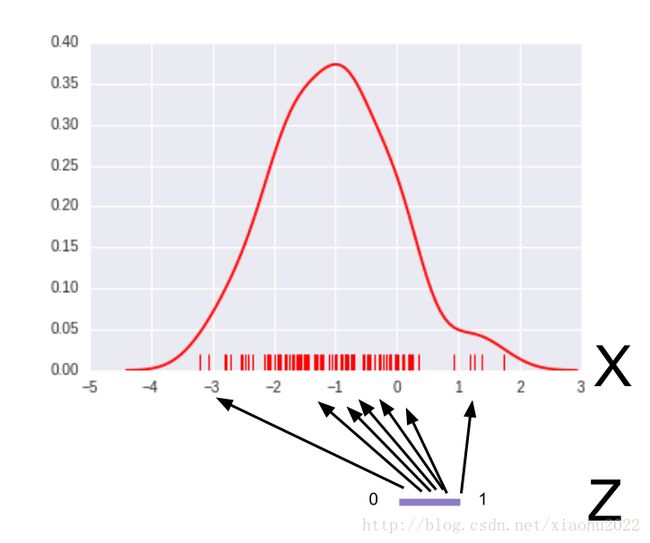
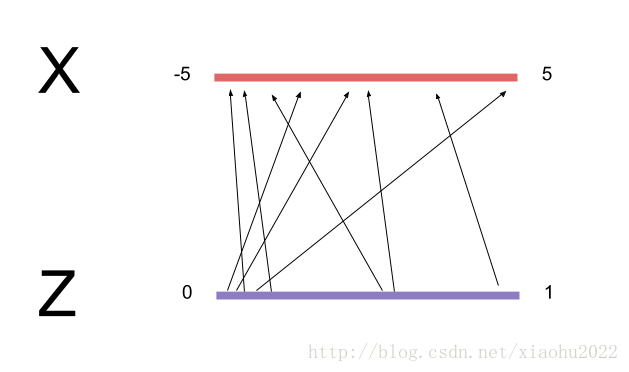
简单地用上面的方法并不能得到好结果,因为每次迭代中我们是独立地从 pdata 和 uniform(0,1) 中抽样。这并不能使得 Z 范围中的邻近点能够映射到 X 范围中的邻近点;在某一小批量训练中,我们可能在训练 G 中发生下面的映射: 0.501→−1.1 , 0.502→0.01 和 0.503→−1.11 。映射线相互交叉很多,这将使转化非常不平稳。更糟糕的是,接下来的小批量训练中,可能发生不同的映射: 0.5015→1.1 , 0.5025→−1.1 和 0.504→1.01 。这表明 G 进行了一个与前面的小批量训练中完全不同的映射,因此优化器不会得到收敛。
为了解决这个问题,我们想最小化从 Z 到 X 的映射线的总长,因为这将使转换尽可能的平顺,而且更加容易学习。 另外一种说法是中将 Z 转化到 X 的“向量丛”在小批量训练中要相互关联。
首先,我们将 Z 的区域拉伸到与 X 区域的大小相同。以 −1 为中心点的正态分布其主要概率分布在 [−5,5] 范围内,所以我们应该从 uniform[−5,5] 来抽样 Z 。这样处理后 G 模型就不需要学习如何将 [0,1] 区域拉伸10倍。 G 模型需要学习的越少,越好。接下来,我们将通过由低到高排序的方式使每个小批量中的 Z 与 X 对齐。
这里我们不是采用 np.random.random.sort()的方法来抽样 Z ,而是采用分层抽样的方式-我们在抽样范围内产生 M 个等距点,然后随机扰动它们。这样处理得到的样本不仅保证其大小顺序,而且可以增加在整个训练空间的代表性。我们接着匹配之前的分层,即排序的 Z 样本对其排序的 X 样本。
当然,对于高维问题,由于在二维或者更高维空间里面对点排序并无意义,所以对其输入空间 Z 与目标空间 X 并不容易。然而,最小化 Z 与 X 流形之间的转化距离仍然有意义[2]。
修改的算法如下:
for i in range(TRAIN_ITERS):
x= np.random.normal(mu,sigma,M).sort()
z= np.linspace(-5.,5.,M)+np.random.random(M)*.01 # stratified
sess.run(opt_d, {x_node: x, z_node: z})
z= np.linspace(-5.,5.,M)+np.random.random(M)*.01
sess.run(opt_g, {z_node: z})这是使这个例子有效的很关键一步:当使用随机噪音作为输入时,未能正确地对齐转化映射线将会产生一系列其它问题,如过大的梯度很早地关闭ReLU神经元,目标函数停滞,或者性能不能随着批量大小缩放。
预处理判别模型
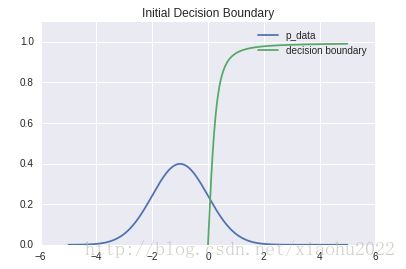
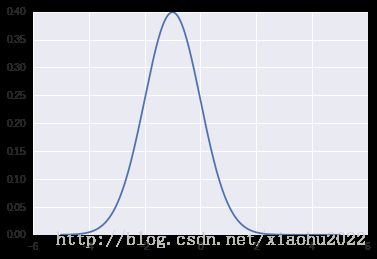
在原始的算法中,GAN是每次通过梯度下降训练 D 模型 k 步,然后训练 G 一步。但是这里发现在训练对抗网络之前,先对 D 预训练很多步更有用,这里使用二次代价函数对 D 进行预训练使其适应 pdata 。这个代价函数相比对数似然代价函数更容易优化(后者还要处理来自 G 的生成样本)。很显然 pdata 就是其自身分布的最优可能性决定边界。
这里是初始的决定边界:
预训练之后:
已经非常接近了,窃喜!
其它的棘手问题建议
- 模型过大容易导致过拟合,但是在这个例子中,网络过大在极小极大目标下甚至不会收敛-神经元在很大的梯度下很快达到饱和。从浅层的小网络开始,除非你觉得有必要再去增加额外的神经元或者隐含层。
- 刚开始我使用的是ReLU神经元,但是这种神经元一直处于饱和状态(也许由于流形对齐问题)。Tanh激活函数好像更有效。
- 我必须要调整学习速率才能得到很好的结果。
结果
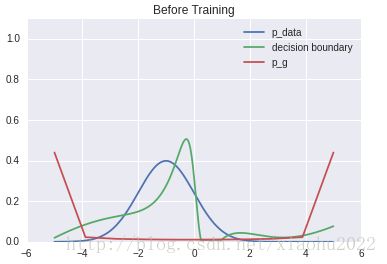
下面是训练之前的 pdata ,预训练后的 D 的决定边界以及生成分布 pg :
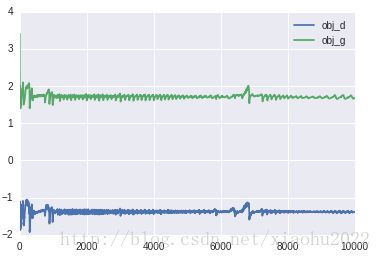
这是代价函数在训练迭代过程中的变化曲线:
训练之后, pg 接近 pdata ,判别器也基对所有 X 一视同仁( D=0.5 ):
这事就完成了训练过程。 G 已经学会如何从 pdata 中近似抽样,以至于 D 已经无法伪数据中分离出真数据。
附录
- 这里是一个关于计算不可分性的更生动例子:假设我们在训练一个超级大的神经网络来从猫脸分布中抽样。真实猫脸的隐含(生成)数据分布包含:1)一只正在出生的猫,2)某人最终拍下了这个猫的照片。显然,我们的神经网络并不是要学习这个特殊的生成过程,因为这个过程并没有涉及真实的猫。然而,如果我们的网络能够产生无法与真实的猫图片相区分的图片(在多项式时间计算资源内)那么从某种意义上说这些照片与正常的猫照片一样合法。在图灵测试,密码学与假劳力士的背景下,这值得深思。
- 可以从过拟合的角度看待过量的映射线交叉,学习到的预测或者判别函数已经被样本数据以一种“矛盾”的方式扭曲了(例如,一张猫的照片被分类为狗)。正则化方法可以间接地防止过多的“映射交叉”,但是没有显式地使用排序算法来确保学习到的从 Z 空间到 X 空间的映射转化是连续或者对齐的。这种排序机制也许对于提升训练速度非常有效。。。