感知机 MLP 梯度反向传播详细推导

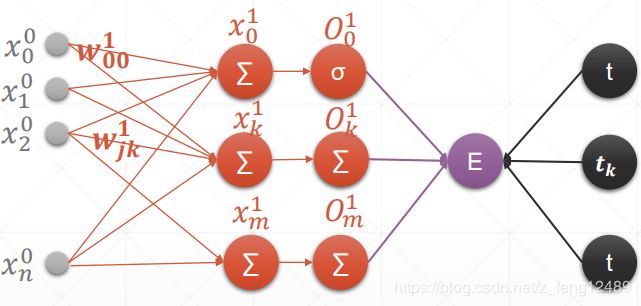
单一输出感知机

x = torch.randn(1, 10)
w = torch.randn(1, 10, requires_grad=True)
o = torch.sigmoid(x@w.t())
o.shape #torch.Size([1, 1])
loss = F.mse_loss(torch.ones(1, 1), o)
loss.shape #torch.Size([]) scalar
loss.backward()
w.grad #tensor([[ 2.1023e-04, -4.6425e-04, 2.1561e-04,...]])

多输出感知机

x = torch.rand(1, 10)
w = torch.rand(2, 10, requires_grad=True)
o = torch.sigmoid(x@w.t())
o.shape #torch.Size([1, 2])
loss = F.mse_loss(torch.ones(1,2), o)
loss #tensor(0.0158, grad_fn=)
loss.backward()
w.grad.shape #torch.Size([2, 10])

链式法则

求导法则

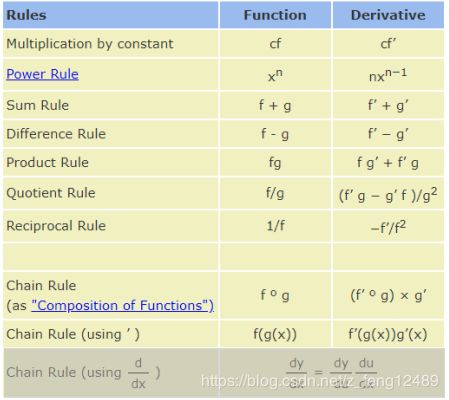
公式
$$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x}$$

x = torch.tensor(1.)
w1 = torch.tensor(2., requires_grad=True)
b1 = torch.tensor(1.)
w2 = torch.tensor(2., requires_grad=True)
b2 = torch.tensor(1.)
y1 = x*w1 + b1
y2 = y1*w2 + b2
dy2_dy1 = torch.autograd.grad(y2, y1, retain_graph=True)[0]
dy1_dw1 = torch.autograd.grad(y1, w1, retain_graph=True)[0]
dy2_dw1 = torch.autograd.grad(y2, w1, retain_graph=True)[0]
dy2_dw1, dy2_dy1, dy1_dw1 #tensor(2.) tensor(2.) tensor(1.)

MLP 反向传播推导

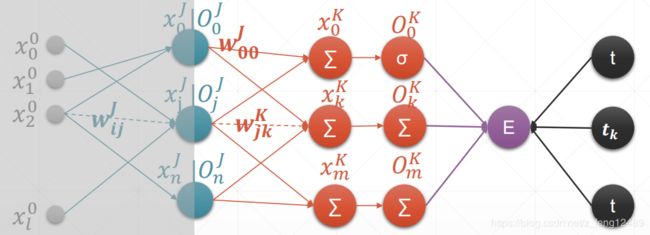
总结：
对 于 一 个 输 出 层 的 节 点 $k\in K$:
$$\frac{\partial E}{\partial w_{jk}}=O_j{\delta }_k$$
这 里，
$${\delta }_k=O_k(1-O_k)(O_k-t_k)$$
对 于 一 个 隐 藏 层 的 节 点 $j\in J$:
$$\frac{\partial E}{\partial w_{ij}}=O_i{\delta }_j$$
这 里，
$${\delta }_j=O_j(1-O_j)\sum _{k\in K}{\delta }_k{w}_{jk}$$

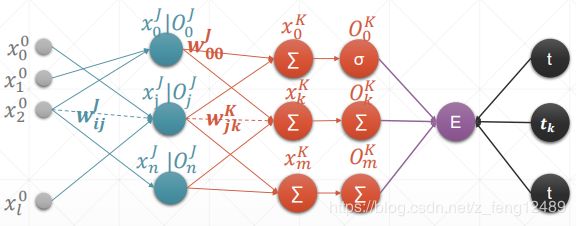
正向传播：
$$O^J-->O^K-->E$$
反向传播：
$${\delta }^K-->\frac{\partial E}{\partial w^K}-->{\delta }^J-->\frac{\partial E}{\partial w^J}-->{\delta }^L-->\frac{\partial E}{\partial w^L}$$

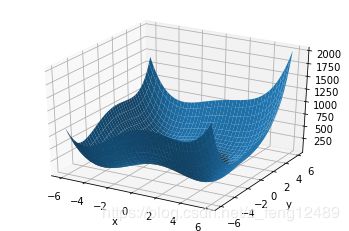
2D 函数优化实例

$$f(x,y)=(x^2+y-11{)}^2+(x+y^2-7{)}^2$$

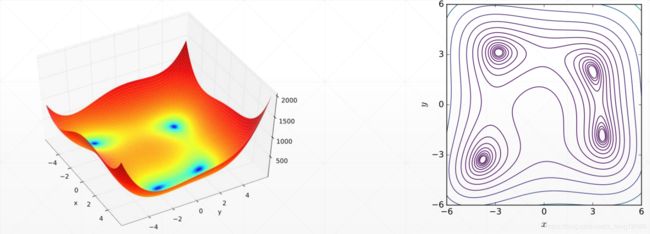
minma:

• f(3,2) = 0
• f(−2.805118,3.131312) = 0
• f(−3.779310,−3.283186) = 0
• f(3.584428,−1.848126) = 0

绘图

import numpy as np
import matplotlib.pyplot as plt
def himmelblau(x):
return (x[0]**2+x[1]-11)**2+(x[0]+x[1]**2-7)**2
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print (x,y range:, x.shape, y.shape)
X, Y = np.meshgrid(x, y)
print (X,Y range:, X.shape, Y.shape)
Z = himmelblau([X,Y])
fig = plt.figure(himmelblau)
ax = fig.gca(projection=3d)
ax.plot_surface(X, Y, Z)
#ax.view_init(60, -30)
ax.set_xlabel(x)
ax.set_ylabel(y)
plt.show()

优化

import torch
x = torch.tensor([0., 0.], requires_grad=True)
optimizer = torch.optim.Adam([x], lr=1e-3) # 建立梯度更新式 x:=x-grad x
for step in range(20000):
pred = himmelblau(x) #得到预测值
optimizer.zero_grad() #清零梯度值
pred.backward() #得到 x 的梯度
optimizer.step() #更新 x 梯度
if step % 2000 == 0:
print (step : x = , f(x) = .format(step, x.tolist(), pred.item()))