吴恩达机器学习第四次作业(python实现):BP神经网络
BP神经网络
import numpy as np
from scipy.io import loadmat
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
import scipy.optimize as opt
import time
def raw_data(path):
data=loadmat(path)
return data
def sigmoid(z):
return 1/(1+np.exp(-z))
# 随机生成100张图片
def random_100_image(x):
indexs=np.random.choice(x.shape[0],100)
images=x[indexs]
# 将幕布分成10x10份,每一份尺寸是10x10
fig,axs=plt.subplots(10,10,sharex=True,sharey=True,figsize=(10,10))
for row in range(10):
for col in range(10):
axs[row,col].matshow(images[row*10+col].reshape(20,20),cmap='gray_r')
plt.xticks([])
plt.yticks([])
plt.show()
# 将y由列向量转换为矩阵
def matrix_y(y):
mat_y=[]
for i in y:
v_y=np.zeros(10)
v_y[i-1]=1
mat_y.append(v_y)
return np.array(mat_y)
# 将两个二维矩阵合并为一个一维矩阵,针对theta以及j的偏导数D
def de_dimension(m1,m2):
return np.r_[m1.ravel(),m2.ravel()]
# 将一个一维矩阵拆成两个二维矩阵,针对theta和theta的偏导
def up_dimension(theta):
theta1 = theta[:401 * 25].reshape(401, 25)
theta2 = theta[401 * 25:].reshape(26, 10)
return theta1,theta2
# 三层神经网络(400,25,10),前向传播
def feed_forward(theta,x):
theta1,theta2=up_dimension(theta)
a1=x
z2=a1.dot(theta1)
a2=sigmoid(z2)
a2=np.c_[np.ones(a2.shape[0]),a2]
z3=a2.dot(theta2)
a3=sigmoid(z3)
return a1,z2,a2,z3,a3
# 代价函数,用for循环实现,此方法速度较慢
def cost_fun(theta,x,y):
a1,z2,a2,z3,h=feed_forward(theta,x)
j=0
for i in range(len(x)):
first=y[i].dot(np.log(h[i]))
second=(1-y[i]).dot(np.log(1-h[i]))
j=j+first+second
j=j/-len(x)
return j
# 代价函数,向量化实现,推荐
def cost_fun_vector(theta,x,y):
a1, z2, a2, z3, h = feed_forward(theta, x)
j=np.sum(y*(np.log(h))+(1-y)*(np.log(1-h)))/(-len(x))
return j
# 正则化代价函数,向量化实现,推荐
def regularized_cost_vector(theta,x,y,lam=1):
theta1, theta2 = up_dimension(theta)
t=np.sum(np.power(theta1,2))+np.sum(np.power(theta2,2)) # 此处需要考虑theta第一行
t1=t*lam/(2*len(x))
return cost_fun_vector(theta,x,y)+t1
# 正则化代价函数,含有for循环速度较慢
def regularized_cost(theta,x,y,lam=1):
theta1,theta2=up_dimension(theta)
t=np.sum(np.power(theta1,2))+np.sum(np.power(theta2,2))
t1=t*lam/(2*len(x))
return cost_fun(theta,x,y)+t1
# sigmoid函数对z求偏导
def partial_sigmoid(z):
return sigmoid(z)*(1-sigmoid(z))
# 反向传播:代价函数第一项对theta求偏导
def gradient(theta,x,y):
a1, z2, a2, z3, h=feed_forward(theta,x)
theta1,theta2=up_dimension(theta)
d3=h-y # (5000, 10)
# 由于维度问题,需要删去theta2的一列
d2= d3 @ (theta2.T[:, 1:]) * partial_sigmoid(z2) # (5000, 25)
D2=(a2.T)@d3 # (26, 10),theta2的偏导数
D1=(a1.T)@d2 # (401, 25),theta1的偏导数
D=de_dimension(D1,D2)/len(x)
return D
# 正则化的代价函数对theta求偏导
def regularized_gradient(theta,x,y,lam=1):
m=len(x)
D = gradient(theta, x, y)
theta1,theta2=up_dimension(theta)
theta1[0]=0
theta2[0]=0
'''
D1,D2=up_dimension(D)
D1=D1+theta1*lam/m
D2=D2+theta2*lam/m
reg_D=de_dimension(D1,D2)
'''
theta=de_dimension(theta1,theta2)
reg_D=D+theta*lam/m
return reg_D
# 梯度检验
def gradient_check(theta,x,y,e=0.0001):
p_theta=[] # 存放每一个theta的偏导数
for i in range(len(theta)):
theta1,theta2=up_dimension(theta)
list1=np.array(range(0,theta1.shape[1]))
list2=np.array(range(theta1.size,theta1.size+theta2.shape[1]))
add=theta.copy()
sub=theta.copy()
add[i]=add[i]+e
sub[i]=sub[i]-e
"""
用偏导数的定义求偏导,此处强烈建议用向量化的代价函数,如果用循环的代价函数,循环次数为5k万+次
用循环的代价函数,执行时间30+min,向量化大概8min左右
"""
if i in list1:
p_t = (cost_fun_vector(add, x, y) - cost_fun_vector(sub, x, y)) / (2 * e)
elif i in list2:
p_t = (cost_fun_vector(add, x, y) - cost_fun_vector(sub, x, y)) / (2 * e)
else:
p_t=(regularized_cost_vector(add,x,y)-regularized_cost_vector(sub,x,y))/(2*e)
p_theta.append(p_t)
p_thetam=np.array(p_theta)
reg_D=regularized_gradient(theta,x,y)
# 通常用欧氏距离衡量
difference=np.linalg.norm(reg_D-p_thetam)/(np.linalg.norm(reg_D)+np.linalg.norm(p_thetam))
print("梯度检测误差(小于0.0001(e)合格):",difference)
# 预测结果
def predict(theta,x):
a1, z2, a2, z3, h=feed_forward(theta,x)
# 从h中的每一行选择最大的值,将其下标+1放入y中
y=np.argmax(h,axis=1)+1
return y
# 根据行列随机生成theta,范围是-0.3~0.3,一个生成row*col个元素
def random_theta(row,col):
return np.array(np.random.uniform(-0.3,0.3,row*col)).reshape(row,col)
def main():
start = time.process_time()
rawdata=raw_data('venv/lib/dataset/ex3data1.mat')
x1=rawdata['X']
x=np.c_[np.ones(x1.shape[0]),x1]
y1=rawdata['y'].ravel()
y=matrix_y(y1)
random_100_image(x1)
# print(x.shape,y.shape) # (5000, 401) (5000, 10)
theta1=random_theta(401,25)
theta2=random_theta(26,10)
# print(theta1.shape,theta2.shape) # (401, 25) (26, 10)
theta=de_dimension(theta1,theta2)
gradient_check(theta,x,y) # 确定正确后立刻关闭,耗时,慎用
result=opt.minimize(fun=regularized_cost_vector,x0=theta,args=(x,y),method='tnc',jac=regularized_gradient)
theta=result.x
print(classification_report(y1,predict(theta,x)))
end = time.process_time()
print("Program run time is",(end - start)/60, "minutes")
'''
theta=raw_data('venv/lib/dataset/ex3weights.mat')
theta=de_dimension(theta['Theta1'].T,theta['Theta2'].T)
print(regularized_cost(theta,x,y))
'''
main()
随机生成100张图片
先从0~5000中随机挑选出100张图片(选择100个数字当作x矩阵的行下标),然后对选择的行进行reshape到(20,20),转化为灰度图像输出即可
# 随机生成100张图片
def random_100_image(x):
indexs=np.random.choice(x.shape[0],100)
images=x[indexs]
# 将幕布分成10x10份,每一份尺寸是10x10
fig,axs=plt.subplots(10,10,sharex=True,sharey=True,figsize=(10,10))
for row in range(10):
for col in range(10):
axs[row,col].matshow(images[row*10+col].reshape(20,20),cmap='gray_r')
plt.xticks([])
plt.yticks([])
plt.show()

然后我们要做的是随机生成theta,一共三层网络,所以要生成两个theta矩阵
# 根据行列随机生成theta,范围是-0.3~0.3,一个生成row*col个元素
def random_theta(row,col):
return np.array(np.random.uniform(-0.3,0.3,row*col)).reshape(row,col)
theta1=random_theta(401,25)
theta2=random_theta(26,10)
然后我们要将这两个theta合并为一个theta向量,后面高级优化方法会用
# 将两个二维矩阵合并为一个一维矩阵,针对theta以及j的偏导数D
def de_dimension(m1,m2):
return np.r_[m1.ravel(),m2.ravel()]
有合并就要有分离
# 将一个一维矩阵拆成两个二维矩阵,针对theta和theta的偏导
def up_dimension(theta):
theta1 = theta[:401 * 25].reshape(401, 25)
theta2 = theta[401 * 25:].reshape(26, 10)
return theta1,theta2
此时我们将theta合并
theta=de_dimension(theta1,theta2)
还有一件事,我们要将y向量转换为矩阵,其实就是将y的值所对应的位置变为1,其他为0,比如y是3,转为为[00300···]
# 将y由列向量转换为矩阵
def matrix_y(y):
mat_y=[]
for i in y:
v_y=np.zeros(10)
v_y[i-1]=1
mat_y.append(v_y)
return np.array(mat_y)
准备就绪,接下来要做的事就是前向传播,不多说,上次作业已经写过
# 三层神经网络(400,25,10),前向传播
def feed_forward(theta,x):
theta1,theta2=up_dimension(theta)
a1=x
z2=a1.dot(theta1)
a2=sigmoid(z2)
a2=np.c_[np.ones(a2.shape[0]),a2]
z3=a2.dot(theta2)
a3=sigmoid(z3)
return a1,z2,a2,z3,a3
然后,代价函数,这里是向量化实现,源码里有for循环实现
# 代价函数,向量化实现,推荐
def cost_fun_vector(theta,x,y):
a1, z2, a2, z3, h = feed_forward(theta, x)
j=np.sum(y*(np.log(h))+(1-y)*(np.log(1-h)))/(-len(x))
return j
正则化代价函数
# 正则化代价函数,向量化实现,推荐
def regularized_cost_vector(theta,x,y,lam=1):
theta1, theta2 = up_dimension(theta)
t=np.sum(np.power(theta1,2))+np.sum(np.power(theta2,2)) # 此处需要考虑theta第一行
t1=t*lam/(2*len(x))
return cost_fun_vector(theta,x,y)+t1
关键来了,反向传播,此时要用到sigmoid函数的导数,很容易求
# sigmoid函数对z求偏导
def partial_sigmoid(z):
return sigmoid(z)*(1-sigmoid(z))
接下来就是 ∂ J ∂ Θ \frac{\partial J}{\partial \Theta } ∂Θ∂J,这是重点
# 反向传播:代价函数第一项对theta求偏导
def gradient(theta,x,y):
a1, z2, a2, z3, h=feed_forward(theta,x)
theta1,theta2=up_dimension(theta)
d3=h-y # (5000, 10)
# 由于维度问题,需要删去theta2的一列
d2= d3 @ (theta2.T[:, 1:]) * partial_sigmoid(z2) # (5000, 25)
D2=(a2.T)@d3 # (26, 10),theta2的偏导数
D1=(a1.T)@d2 # (401, 25),theta1的偏导数
D=de_dimension(D1,D2)/len(x)
return D
然后正则化
# 正则化的代价函数对theta求偏导
def regularized_gradient(theta,x,y,lam=1):
m=len(x)
D = gradient(theta, x, y)
theta1,theta2=up_dimension(theta)
theta1[0]=0
theta2[0]=0
'''
D1,D2=up_dimension(D)
D1=D1+theta1*lam/m
D2=D2+theta2*lam/m
reg_D=de_dimension(D1,D2)
'''
theta=de_dimension(theta1,theta2)
reg_D=D+theta*lam/m
return reg_D
这个时候就完成反向传播了,不过不要着急,还有梯度检验,防止出错,梯度检验实际上是用导数的定义 lim ε → 0 f ( θ + ε ) − f ( θ − ε ) 2 ε ≈ d f d θ \lim_{\varepsilon \to 0}\frac{f(\theta +\varepsilon )-f(\theta-\varepsilon )}{2\varepsilon }\approx \frac{df}{d\theta } limε→02εf(θ+ε)−f(θ−ε)≈dθdf,我们只需将 ε \varepsilon ε取很小即可,但也不要太小,记住检验完成后若果正确就关闭,太耗时。
# 梯度检验
def gradient_check(theta,x,y,e=0.0001):
p_theta=[] # 存放每一个theta的偏导数
for i in range(len(theta)):
theta1,theta2=up_dimension(theta)
list1=np.array(range(0,theta1.shape[1]))
list2=np.array(range(theta1.size,theta1.size+theta2.shape[1]))
add=theta.copy()
sub=theta.copy()
add[i]=add[i]+e
sub[i]=sub[i]-e
"""
用偏导数的定义求偏导,此处强烈建议用向量化的代价函数,如果用循环的代价函数,循环次数为5k万+次
用循环的代价函数,执行时间30+min,向量化大概8min左右
"""
# 当theta是第一行(theta0)时,认为j对theta的偏导数为0,
# 即不惩罚第一项,所以此时不需要对theta求偏导
if i in list1:
p_t = (cost_fun_vector(add, x, y) - cost_fun_vector(sub, x, y)) / (2 * e)
elif i in list2:
p_t = (cost_fun_vector(add, x, y) - cost_fun_vector(sub, x, y)) / (2 * e)
else:
p_t=(regularized_cost_vector(add,x,y)-regularized_cost_vector(sub,x,y))/(2*e)
p_theta.append(p_t)
p_thetam=np.array(p_theta)
reg_D=regularized_gradient(theta,x,y)
# 通常用欧氏距离衡量,此时误差小于epsilon即认为正确
difference=np.linalg.norm(reg_D-p_thetam)/(np.linalg.norm(reg_D)+np.linalg.norm(p_thetam))
print("梯度检测误差(小于0.0001(e)合格):",difference)
梯度检验结果: 接下来就可以反向传播了 预测 精度,召回率,f1-score 最后结果95%多的样子

运行了9分钟
关于结果误差如何确定,通常采用 d i f f e r e c e = ∥ g r a d − g r a d a p p r o x ∥ 2 ∥ g r a d ∥ 2 + ∥ g r a d a p p r o x ∥ 2 differece= \frac{\left \| grad-gradapprox \right \|_{2}}{\left \| grad \right \|_{2}+\left \| gradapprox \right \|_{2}} differece=∥grad∥2+∥gradapprox∥2∥grad−gradapprox∥2
其中 ∥ ∥ 2 \left \| \right \|_{2} ∥∥2为二范数,分子为欧式距离,该方法确定的误差,若differenceresult=opt.minimize(fun=regularized_cost_vector,x0=theta,args=(x,y),method='tnc',jac=regularized_gradient)
theta=result.x
# 预测结果
def predict(theta,x):
a1, z2, a2, z3, h=feed_forward(theta,x)
# 从h中的每一行选择最大的值,将其下标+1放入y中
y=np.argmax(h,axis=1)+1
return y
print(classification_report(y1,predict(theta,x)))
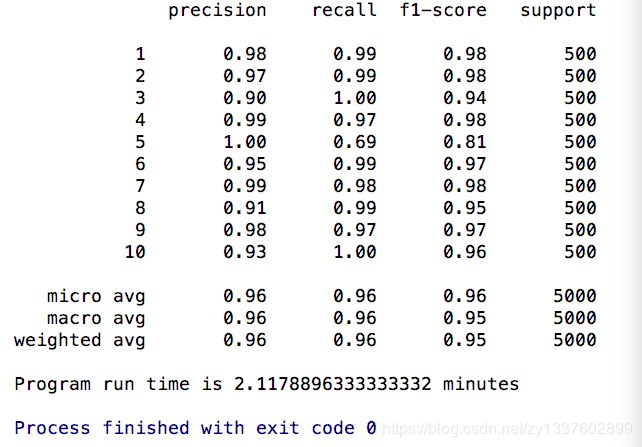
关于report结果,如果不会看的话,看这里classification_report结果说明
另外,由于每次theta初始化不同,执行时间和结果都会有差异,但差别不大。