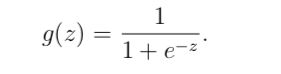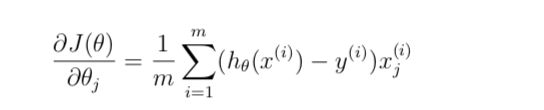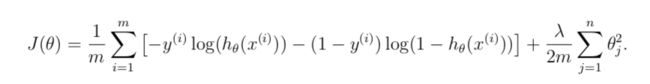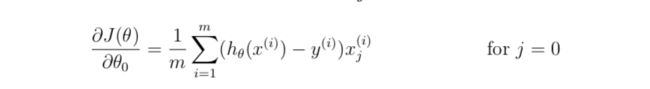吴恩达机器学习第二次编程作业----LogisticsRegression
作业的问题的背景PDF文件里面有,不再赘述。
1:Logistic Regression
1.1 Visualizing the data
data = load('ex2data1.txt');
X = data(:, [1, 2]); y = data(:, 3);
plotData(X, y); %plotData文件按照pdf给的去补全就行。如图:
1.2 Implementation
补全 sigmoid.m文件。
根据公式可得:
g = 1./(1+(exp(-1*z)));
1.2.2 Cost function and gradient
补全 costFunction.m文件里面的代价函数J和对于theta_J的偏微分。
根据公式可得:
J = 1/m*(sum(-y.*log(sigmoid(X*theta))-(1-y).*log(1-sigmoid(X*theta))));
grad = 1/m.*X'*(sigmoid(X*theta)-y);测试代码:
% Compute and display initial cost and gradient
[cost, grad] = costFunction(initial_theta, X, y);符合要求。
1.2.3 Learning parameters using fminunc
接下来调用fminunc函数来计算最优解。
% Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);
% Run fminunc to obtain the optimal theta
% This function will return theta and the cost
[theta, cost] = ...
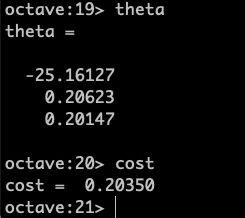
fminunc(@(t)(costFunction(t, X, y)), initial theta, options);得到:
接下来测试一下:
x_test=[1, 45, 85];
z=x_test*theta;
predict = sigmoid(z)得到:
符合要求。
做预测:
补全predict.m文件
实现方法一:
p = sigmoid(X * theta)
index_1 = find(p >= 0.5)
p(index_1) = 1
index_0 = find(p < 0.5)
p(index_0) = 0实现方法二:
k = find(sigmoid(X*theta) >= 0.5)
p(k) = 1然后在终端输入:
p = predict(theta, X);
mean(double(p == y)) * 100 % p==y 如果相等则对应项为1,不想等则为0符合要求。
2 Regularized logistic regression
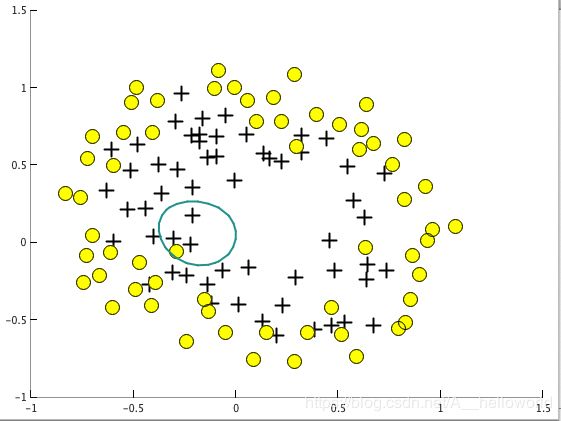
1:画图:
data = load('ex2data2.txt');
X = data(:, [1, 2]); y = data(:, 3);
plotData(X, y);如图:
2:Feature mapping
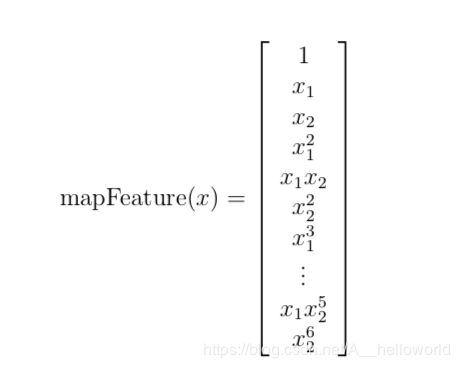
这一步主要是生成多项式。
多项式如下:
因为有很多很高次的项,为了避免出现过拟合的情况,需要正则化costFunction。
3:Cost function and gradient
补全costFunctionReg.m文件。
公式:
costFunction:
grad:
J = 1/m*sum(-y.*log(sigmoid(X*theta))-(1-y).*log(1-sigmoid(X*theta)))+lambda/(2*m)*(sum(theta.^2) - theta(1)^2); % 不需要对theta1进行正则化
grad = 1/m*X'*(sigmoid(X*theta)-y) + lambda/m*theta;
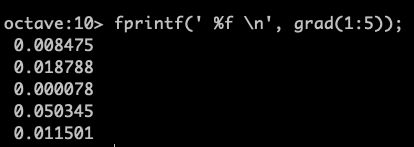
grad(1) = 1/m*X(:,1)'*(sigmoid(X*theta)-y);完成后测试下:
[cost, grad] = costFunctionReg(initial_theta, X, y, lambda);grad有点长,只列出前五个。
4:使用fminunc函数求得最优解,然后画图:
initial_theta = zeros(size(X, 2), 1);
lambda = 1;
options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, J, exit_flag] = fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);
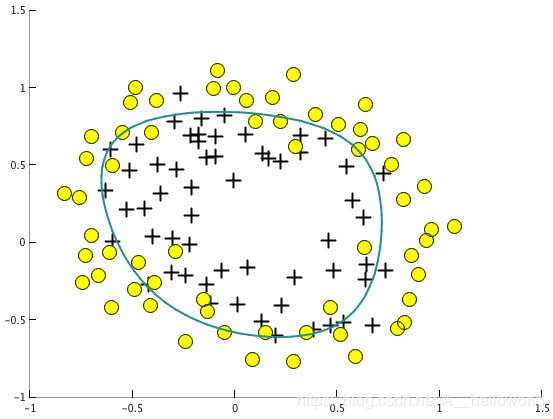
plotDecisionBoundary(theta, X, y);
如图:
做predict:
p = predict(theta, X);
mean(double(p == y)) * 100符合要求。
5: 使用不同的lambda来理解下正则化如何有利于防止过拟合的现象。
由公式可知,如果lambda过大,将会对theta造成很大的抑制效果,也就是theta会很小,这样就不会出现过拟合的现象,但是会使得拟合的效果不好。
如果lambda过小,将无法抑制theta,导致theta会比较大,这样就会导致过拟合的现象。下面分别是lambda=50(Underfitting)和0(Overfitting)的情况。(lambda=100的情况我的电脑无法输出像pdf里面的Decision boundary,我觉得这种情况下,theta太小了,应该是无法输出边界的,所以我选了lambda=50来模拟underfitting的情况)
lambda=50(Underfitting):
lambda=0(Overfitting):