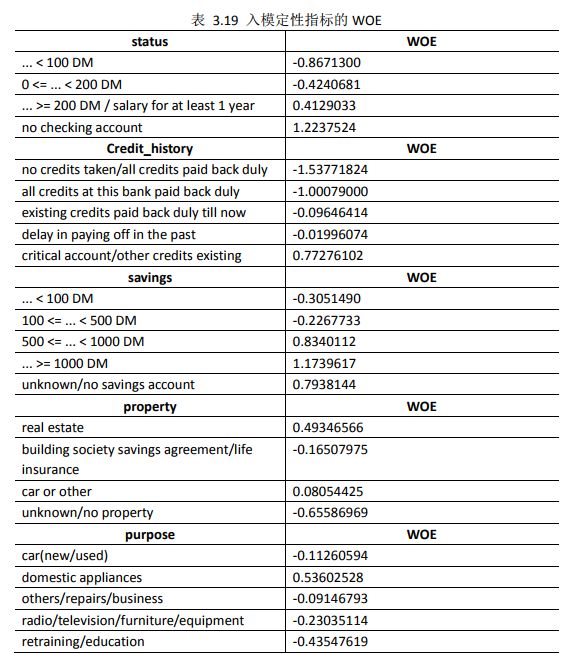
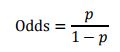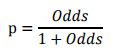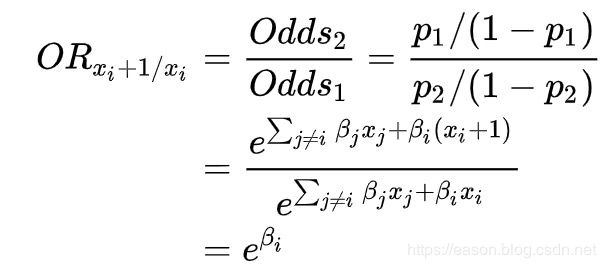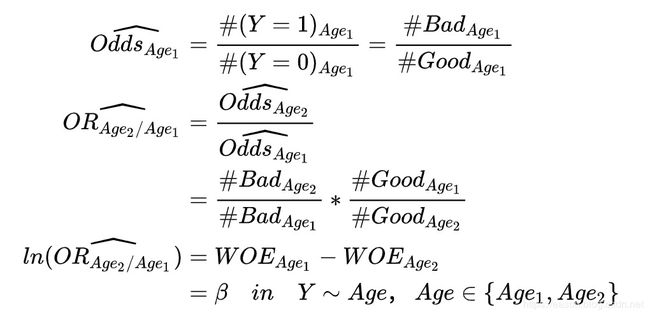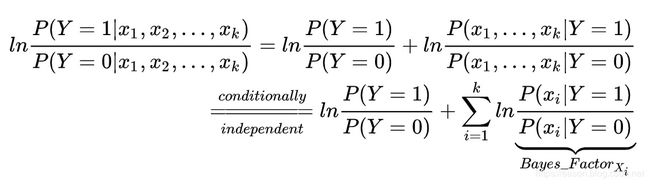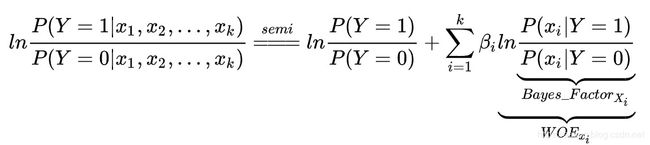评分卡模型开发--WOE值计算

原文链接： https://zhuanlan.zhihu.com/p/30026040

转自：https://cloud.tencent.com/developer/article/1016331

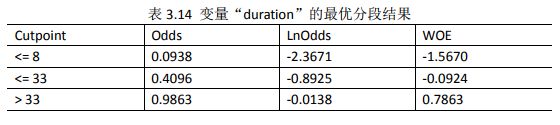
对入模的定量和定性指标，分别进行连续变量分段（对定量指标进行分段），以便于计算定量指标的WOE和对离散变量进行必要的降维。对连续变量的分段方法通常分为等距分段和最优分段两种方法。等距分段是指将连续变量分为等距离的若干区间，然后在分别计算每个区间的WOE值。最优分段是指根据变量的分布属性，并结合该变量对违约状态变量预测能力的变化，按照一定的规则将属性接近的数值聚在一起，形成距离不相等的若干区间，最终得到对违约状态变量预测能力最强的最优分段。 我们首先选择对连续变量进行最优分段，在连续变量的分布不满足最优分段的要求时，在考虑对连续变量进行等距分段。此处，我们讲述的连续变量最优分段算法是基于条件推理树（conditional inference trees, Ctree）的递归分割算法，其基本原理是根据自变量的连续分布与因变量的二元分布之间的关系，采用递归的回归分析方法，逐层递归满足给定的显著性水平，此时获取的分段结果（位于Ctree的叶节点上）即为连续变量的最优分段。其核心算法用函数ctree()表示。 根据表3.13所示的定量入模指标，我们采用上述最优分段算法，得到的最优分段结果分别如下。 对变量“duration”进行最优分段：

#对duration进行最优分段
library(smbinning)
result<-smbinning(df=data,y="credit_risk",x="duration",p=0.05)
result$ivtable

变量“duration”的最优分段结果，如表3.14所示

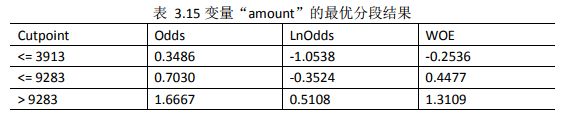
#对amount进行最优分段
result<-smbinning(df=data,y="credit_risk",x="amount")
result$ivtable

#对变量age进行最优分段
result<-smbinning(df=data,y="credit_risk",x="age")
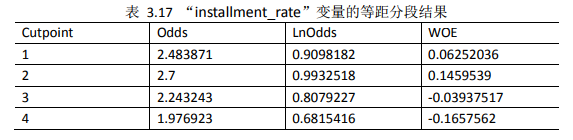
result$ivtable

由于变量“installment_rate”的取值只有四个值，不适用于最优分段算法，只能采用等距分段，等距分段结果如表3.17 所示：

#对变量“installment_rate"的等距分段
install_data<-data[,c("installment_rate","credit_risk")]
tb1<-table(install_data)
total<-list()
for(i in 1:nrow(tb1))
{
  total[i]<-sum(tb1[i,])
}
t.tb1<-cbind(tb1,total)
goodrate<-as.numeric(t.tb1[,"0"])/as.numeric(t.tb1[,"total"])
badrate<-as.numeric(t.tb1[,"1"])/as.numeric(t.tb1[,"total"])
gb.tbl<-cbind(t.tb1,goodrate,badrate)
Odds<-goodrate/badrate
LnOdds<-log(Odds)
tt.tb1<-cbind(gb.tbl,Odds,LnOdds)
WoE<-log((as.numeric(tt.tb1[,"0"])/700)/(as.numeric(tt.tb1[,"1"])/300))
all.tb1<-cbind(tt.tb1,WoE)
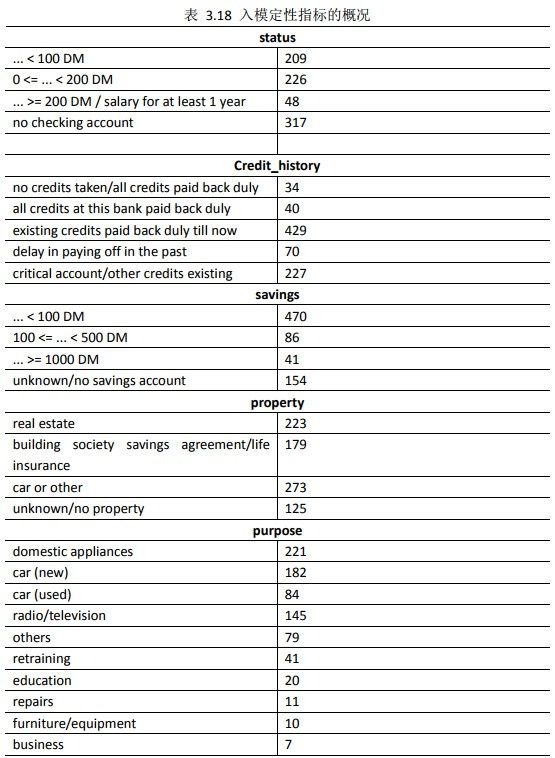
all.tb1

结束对连续变量的分段及其WOE值的计算，接下来我们需要对离散变量做必要的降维处理及其WOE值得计算。我们首先查看下入模的定性指标的概况，如表3.18所示，代码如下：

discrete_data<-data[,c("status","credit_history","savings","purpose",
                       "property","credit_risk")]
summary(discrete_data)

由表3.18所示的入模定性指标的概况可知，定性指标“status” “credit_history”“savings”和“property”的维数最高为5维，最低为4维，而定性指标“purpose”的维数为10维，跟其他定性指标相比，明显高出很多。此时，通常会造成“维数灾难”，需要降维处理。在评级模型开发中的降维处理方法，通常是将属性相似的合并处理，以达到降维的目的。

#对purpose指标进行降维
x<-discrete_data[,c("purpose","credit_risk")]
d<-as.matrix(x)
for(i in 1:nrow(d))
{
  if(as.character(d[i,"purpose"])=="car (new)")
  {
    d[i,"purpose"]<-as.character("car(new/used)")
  }
  if(as.character(d[i,"purpose"])=="car (used)")
  {
    d[i,"purpose"]<-as.character("car(new/used)")
  }
  if(as.character(d[i,"purpose"])=="radio/television")
  {
    d[i,"purpose"]<-as.character("radio/television/furniture/equipment")
  }
  if(as.character(d[i,"purpose"])=="furniture/equipment")
  {
    d[i,"purpose"]<-as.character("radio/television/furniture/equipment")
  }
  if(as.character(d[i,"purpose"])=="others")
  {
    d[i,"purpose"]<-as.character("others/repairs/business")
  }
  if(as.character(d[i,"purpose"])=="repairs")
  {
    d[i,"purpose"]<-as.character("others/repairs/business")
  }
  if(as.character(d[i,"purpose"])=="business")
  {
    d[i,"purpose"]<-as.character("others/repairs/business")
  }
  if(as.character(d[i,"purpose"])=="retraining")
  {
    d[i,"purpose"]<-as.character("retraining/education")
  }
  if(as.character(d[i,"purpose"])=="education")
  {
    d[i,"purpose"]<-as.character("retraining/education")
  }
}

new_data<-cbind(discrete_data[,c(-4,-6)],d)
woemodel<-woe(credit_risk~.,data = new_data,zeroadj=0.5,applyontrain=TRUE)
woemodel$woe

至此，整个模型开发过程中第四步的工作，我们已经基本完成了。可见，该步骤在整个模型开发过程中占据非常重要的位置，定量和定性入模指标的筛选及其WOE值的计算，都会对整个信用风险评分卡产生重要的影响。在模型开发的第五步，我们将使用入模定量指标和入模定性指标的WOE值进行逻辑回归，并详细讲述生成信用风险评级模型标准评分卡的过程。

补充：

WOE的意义（为什么要计算WOE）(https://zhuanlan.zhihu.com/p/30026040)

虽然网上到处都是神经网络、xgboost的文章，但当下的建模过程中（至少在金融风控领域）并没有完全摆脱logistic模型，原因大致有以下几点：

1. logistic模型客群变化的敏感度不如其他高复杂度模型，因此稳健更好，鲁棒性更强。
2. 模型直观。系数含义好阐述、易理解。对金融领域高管以及银行出身的建模专家，变量系数可以跟他们的业内知识做交叉验证，更容易让人信服。
3. 也是基于2的模型直观性，当模型效果衰减的时候，logistic模型能更好的诊断病因

计算woe（以及IV）的意义我所知的有以下几点：

• IV值可以衡量各变量对y的预测能力，用于筛选变量。
• 对离散型变量，woe可以观察各个level间的跳转对odds的提升是否呈线性，而IV可以衡量变量整体（而不是每个level）的预测能力。

当你有千级别或者万级别的字段时，建模前计算IV值是很有必要的。以地区邮编为例，level很多，每个level下样本少，常规的处理是用dummy encoding将n个level的变量拆成n-1个哑变量，然后建模做检验，得到这n-1个哑变量的显著性，再对n-1个哑变量做聚类等处理才能feed in model。如果到最后你不管怎么处理都不太好feed进model，那就白忙了，场面会相当的尴尬。这个时候就体现了事先计算IV值来筛选变量的重要性了。

• 对连续型变量，woe和IV值为分箱的合理性提供了一定的依据。

分箱处理连续型变量会有信息损失，但由于绝大多数情况下连续型变量对odds的提升都不是线性的，这里能产生的负面影响远比信息损失要大，因此一般都需要做分箱处理。

• 用woe编码可以处理缺失值问题。

为了了解WOE，这里分三步简单讲一下对数比率Odds，也就是事件发生和不发生的比例， Odds Ratio，两组Odds的比值，叫做优势比：

由逻辑回归的基本原理，我们将客户违约的概率表示为p，则正常的概率为1-p。因此，可以得到几率，也叫对数比率：

此时，客户违约的概率p可表示为：

OR在逻辑回归中的意义

Odds和Odds ratio在logistic中非常值得重视，因为他们跟参数的interpretation（解释性）密切相关。

在logistic回归中：

逻辑回归模型计算比率如下所示：

其中，用建模参数拟合模型可以得到模型参数β0，β1，…，βn。

OR 表示两组odds的比例，那么我们计算xi和xi+1的OR:

 也就是说，当xi增加一个单位时，odds增加e^beta倍

OR的估计值（Marginal OR）与WOE

一般的，我们可以通过列联表计算Odds和Odds Ratio的估计值。

【值得注意的是】通过列联表算得的OR是指Marginal OR，大家可以将Marginal OR理解为模型y～xi的，这是个单变量回归模型。本文中涉及WOE的OR指的都是Marginal OR。而多元回归中的对应的是Conditional OR。两者是不一样的。

也就是结合OR和WOE,WOE单调实际上就意味着当agei单调上升时，相应的odds也呈现单调递增,对应的p(y=1|agei)也呈单调递增。我们可以用一个更简洁的公式概括上面的计算过程：

可以看出，ln(odds)与woe只差了一个常数而已。 

WOE呈线性&WOE编码 的意义

WOE呈线性是一个很强的条件，比单调要强得多。一般来说是不会这么巧出现线性的情况的，我之所以要提，是因为我们可以通过WOE编码人为地让它呈线性，这个后面再提。

先说WOE呈线性的意义

如果一个变量的不同level（假设各level分别以 0,1,2,3...进行编码）的WOE呈线性，说明该变量每增加一个单位，对Odds产生的影响是一样的。

因此，在某些我们需要对属性变量做dummy encoding的场景下，因为我们不能保证变量从任意leveli跳转到leveli+1时对Odds产生的影响都一样，所以不能用{0,1,2,3...}这样等间距的编码方式。

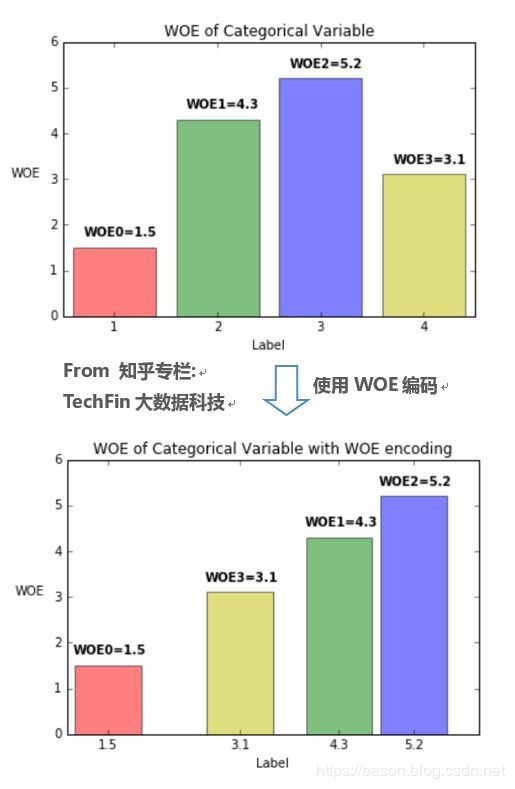
WOE编码的意义

而WOE近似于事先计算了变量各level的Marginal Odds，将对应的WOE取代属性变量的原始值{0,1,2,3...}，即使用WOE编码，可以使得该变量每增加一个单位，Odds就增加相同的值，参考下图。

结论就是：如果使用了WOE编码，当我们对单变量进行回归（Y~Xi）时，可以不做dummy encoding，此时变量的系数恒为1。WOE编码起到了把回归系数“正则化”的作用。

上面WOE解决的问题都是对单变量回归有效，在多元logistic回归里仍然有效么？

答案是无效的，多元logistic回归里的系数并不会因为WOE编码而全部等于1。

WOE也好，IV也好，做的都是单变量分析。我们认为对Y有较好预测能力的变量，在多元回归时仍然会有较好的预测能力。基于此逻辑可以用IV值来对变量的重要性进行排序。

WOE与贝叶斯因子的联系

简单提下贝叶斯因子，就不展开讲了，各位可以上网查Bayes factor。

当变量不止一个的时候，如果任意Xi和Xj关于Y条件独立的话，则有：

条件独立经常跟贝叶斯相关的东西扯上关系，比如说朴素贝叶斯分类器，之所以“朴素”，就是因为各变量关于Y条件独立这一强假设。如果不满足条件独立，那么就会出现多个变量对结果产生协同影响的情况，极其影响结果。

为了弱化条件独立这一个强假设，出现了非完全朴素的贝叶斯分类器（semi-Bayes）

semi-Bayes 总体来说就是用各种规则来对变量进行加权（特别地，当权值是0/1的时候就是进行变量筛选了，并认为筛选后的变量条件独立），以此来抑制相关变量的协同影响。

我们将semi的思想用在上式，便有：

这个就是用WOE编码后的logistic模型。

所以说WOE编码其实也可以从非完全条件独立的贝叶斯因子的角度去看待。