【NOIP2018提高组】D1T2 货币系统
文章目录
- 题目
- 思路
题目
题目描述
在网友的国度中共有 n n n种不同面额的货币,第 i i i种货币的面额为 a [ i ] a[i] a[i],你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 n n n、面额数组为 a [ 1... n ] a[1...n] a[1...n]的货币系统记作 ( n , a ) (n,a) (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x x x都应该可以被表示出,即对每一个非负整数 x x x,都存在 n n n个非负整数 t [ i ] t[i] t[i]满足 a [ i ] × t [ i ] a[i]\times t[i] a[i]×t[i]的和为 x x x。然而,在网友的国度中,货币系统可能是不完善的,即可能存在金额 x x x不能被该货币系统表示出。例如在货币系统 n = 3 n=3 n=3, a = [ 2 , 5 , 9 ] a=[2,5,9] a=[2,5,9]中,金额 1 , 3 1,3 1,3就无法被表示出来。
两个货币系统 ( n , a ) (n,a) (n,a)和 ( m , b ) (m,b) (m,b)是等价的,当且仅当对于任意非负整数 x x x,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 ( m , b ) (m,b) (m,b),满足 ( m , b ) (m,b) (m,b)与原来的货币系统 ( n , a ) (n,a) (n,a)等价,且 m m m尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 m m m。
输入输出格式
输入格式
输入文件的第一行包含一个整数 T T T,表示数据的组数。
接下来按照如下格式分别给出 T T T组数据。 每组数据的第一行包含一个正整数 n n n。接下来一行包含 n n n个由空格隔开的正整数 a [ i ] a[i] a[i]。
输出格式
输出文件共有 T T T行,对于每组数据,输出一行一个正整数,表示所有与 ( n , a ) (n,a) (n,a)等价的货币系统 ( m , b ) (m,b) (m,b)中,最小的 m m m。
输入输出样例
输入样例:
2
4
3 19 10 6
5
11 29 13 19 17
输出样例:
2
5
说明
在第一组数据中,货币系统 ( 2 , [ 3 , 10 ] ) (2, [3,10]) (2,[3,10])和给出的货币系统 ( n , a ) (n, a) (n,a)等价,并可以验证不存在 m < 2 m<2 m<2的等价的货币系统,因此答案为 2 2 2。 在第二组数据中,可以验证不存在 m < n m<n m<n的等价的货币系统,因此答案为 5 5 5。
数据规模与约定
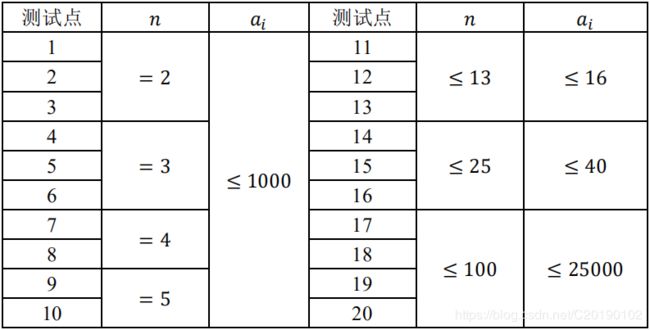
对于 100 % 100\% 100%的数据,满足 1 ≤ T ≤ 20 1\leq T\leq 20 1≤T≤20, n , a [ i ] ≥ 1 n,a[i]\geq 1 n,a[i]≥1。
思路
先排个序。
如果当前面值能由前面的面值凑出,当前面值就可以不要了。
完全背包即可。
本来以为多年准备一场空,不开滚动见祖宗,结果在洛谷上还过了。
其实考场上都不知道是完全背包,只知道是DP。
考场代码:
#include