算法学习之路(一)——数据抽象
前言
本文根据Algorithms(《算法》)一书,介绍算法的基础知识,围绕数据抽象,介绍了包括背包、队列和栈三种集合类数据类型的定义以及代码实现,最后讲解了链表的相关定义以及使用链表实现集合类数据类型。
准备工作
在开始聊数据抽象之前,我们需要先弄清楚几个概念,都是很基础的东西,不过话说回来,算法本就该是编程的基础,这些基础的概念是我们开始学习算法的前提:
1、什么是数据类型?
2、什么是数据抽象?
3、面向对象编程中的“对象”指的是什么?
4、Java中的基本类型和引用类型;
5、什么是抽象数据类型?它能解决什么样的问题?
对于这几个问题,我们一条一条地来聊。(这一系列文章围绕算法而写,基于Java语言。记得当年在大学里学算法时更多是围绕C++,不过使用Java语言来描述可能会简单一些,再者对于算法的学习语言都不重要,我们把注意力更多地放在算法本身)
首先,数据类型是指一组值和一组对这些值的操作的集合,而数据抽象则是指对数据类型的定义和使用过程;
面向对象编程是当今编程的一个重要概念,我们可以将其理解为将事物的属性和行为进行提取抽象为数据类型,进而对抽象出来的数据类型的实体进行编程,于是我们可以认为“对象”即是数据类型的值的实体;
Java中使用class来定义被称为“引用类型”的数据类型,与基本类型对应,说到这里,不如来回忆一下Java的基本类型,byte(-2^7~2^7-1)、short(-2^15~2^15-1)、int(-2^31~2^31-1)、long(-2^63~2^63-1)、double(双精度64位浮点数)、float(单精度32位浮点数)、boolean(布尔值)、char(单一的16位Unicode字符),如果在编程中仅仅使用基本类型,那很大程度上我们的程序仅仅停留在解决算数层面的问题,在加入引用类型后,我们可以将任何事物抽象为对象,编程将会变得更加灵活和自由;
抽象数据类型(ADT)是一种能对使用者隐藏数据表示的数据类型。在使用抽象数据类型时,使用者只需要关心API描述的操作而非数据的表示,我们往往用它来定义问题和描述算法和数据结构。
在明白了这几个问题后,我们就可以正式开始这一章算法基础的学习了,接下来的内容会相当枯燥,算法与数据结构是我在大学时相当讨厌的一门课。不过相信我,这些东西会很有用。
从背包、队列和栈说起
单独将数据抽象拎出来讲可能显得太单薄了,我们来从可迭代的数据类型认识数据抽象,也就是集合。在理解了上文的种种概念后,我们来看看集合,这是一种数据类型,它的值就是一组对象的集合,而它所有的操作都是关于添加、删除或是访问集合中的对象。接下来要说的是三种这样的数据类型:背包(Bag)、队列(Queue)和栈(Stack)。
抽象
上文已经说过了,数据抽象是对数据类型定义和使用的过程,而抽象数据类型是指对使用者隐藏数据表示的数据类型,我们现在所说的背包、队列和栈都是抽象数据类型,我们只关注其API的描述,所以我们需要抽象出我们需要的API。这个过程就是数据抽象的实现。
背包
先来认识一下,集合型数据类型“背包”,指的是一种不支持从中删除元素的集合数据类型,构造它的目的就是帮助用例收集元素并迭代遍历所有收集到的元素。提取出定义中的关键信息:
·不支持删除:不用定义删除相关的方法
·可以帮助用例收集元素:需要add方法
·可以迭代遍历收集到的元素:需要实现Iterable接口
·我们可能需要知道集合中是否有元素(isEmpty)以及集合中元素的数量(size)
于是我们可以定义背包的API如下:
| public class Bag |
||
| Bag() | 构造器,创建一个空背包 | |
| void | add(Item item) | 添加一个元素 |
| boolean | isEmpty() | 背包是否为空 |
| int | size() | 背包中的元素数量 |
队列
队列一般是指先进先出队列(FIFO,大学里算法课熟悉的概念),是一种基于先进先出策略的集合类型。自然世界的很多场景都遵循先进先出原则,无论是早餐店排队的人群,还是收费站前排队的车,我们都可以将它们看做先进先出队列。优先服务等待最久的,这就是先进先出策略的原则。在程序中使用队列的主要原因是在用集合保存元素的同时还要维护它们的相对顺序,即保证它们的出列顺序和入列顺序一致。根据定义我们可以知道,与背包相比,队列中的元素是顺序排列的,新添加的元素排在末尾,同时还具有一个出列(删除一个元素)的方法。于是队列的API定义如下:
| public class Queue |
||
| Queue() | 构造器,创建一个空队列 | |
| void | enqueue(Item item) | 向队列中添加一个元素 |
| Item | dequeue() | 删除最早添加的元素 |
| boolean | isEmpty() | 队列是否为空 |
| int | size() | 队列中的元素数量 |
栈
这里所说的栈即“下压栈”,与队列相反,这是一种基于后进先出策略的集合类型(LIFO,后进先出策略)。记得读书那会儿,总结出了一套学问,那就是考试的时候绝不能当交卷早的,但也不能太晚——交早了试卷沉底,老师批阅最后几张会比较仔细;交晚了试卷会在最上边儿,前几张试卷老师也会格外上心;只有在中间的,有些小错误小马虎可能在就会被老师不经意错过了。大家可以发现这个场景中,考试收卷即使遵循了后进先出策略,类似的场景还有我们的电子邮箱,新邮件总是在最上面最先被阅读,我们可以把一摞试卷当做一个下压栈,也可以把电子邮箱当做一个下压栈。下压栈的API定义如下:
| public class Stack |
||
| Stack() | 构造器,创建一个空栈 | |
| void | push(Item item) | 压栈,创建一个新元素 |
| Item | pop() | 栈顶元素出栈,删除一个元素 |
| boolean | isEmpty() | 栈是否为空 |
| int | size() | 栈中的元素数量 |
认识泛型
这一小节对于大多数Java程序员来说可能太基础了,如果你认为你已经熟知泛型的话就可以跳过。
我们先来思考一个问题,抽象数据类型是为了解决怎样的问题而存在的,就拿集合来说——对于描述早餐排队问题,我们可以建立一个集合BreakfastQueue来描述排队的人群;对于超市排队付费我们可以建立一个集合MarketQueue来描述排队的人群……在无数的场景我们都可以单独地为它们建立描述它们的集合,我们当然可以视场景来解决问题——不过,你会不会觉得这样多此一举?无论是人的队列、动物的队列、车辆的队列还是信息的队列等等,站在集合的角度来讲,它们都是一堆对象的集合,对于这些队列它们的行为模式是完全一致的,区别仅仅在于它们装的是什么对象——对于集合的操作,我们是不care它里面的对象的,我们只会在编写用例的时候才会从集合中取出具体对象进行操作。于是我们可以把人的队列、动物的队列、车辆的队列还是信息的队列等等统一抽象为同一种队列Queue,这又可以涉及到面向对象编程中的一个重要特性——封装,使用数据类型的实现封装数据,以简化方法的实现和隔离用例开发——这也是数据抽象在编程中之所以这么重要的原因。
可是如何让一个集合类能够存储任意的数据类型呢?这就要依靠泛型了。
参照上面的API定义,在类名后面都跟有"
自动装箱
Algorithms一书在这一章恰好提到了这个概念,简单解释一下,上文中我们讲到了泛型,Item可以被替换成任何实际的数据类型,但事实上这里有一个前提,实际的数据类型必须为引用类型而非基本类型,这就引出了个问题:我们的用例中要实现一个装有int对象的集合该怎么办?
Java为每种基本类型都提供了对应的封装类型,封装类型也是引用类型。在处理赋值语句、方法的参数和算术或逻辑表达式时,Java会自动在封装类型和对应的原始基本类型之间进行转换,将一个基本类型转换为封装类型便被称为自动装箱,相反地,将封装类型转换为基本类型则被称为自动拆箱。
可迭代的集合类型
可以看到,以上三种集合类型都实现了Iterable接口,这是为了是它们成为可迭代的数据类型。如果仅仅是存放数据,那集合类就显得太鸡肋了,很多时候,我们都希望能对集合进行迭代以访问集合中的所有数据对其进行统一的处理。
集合类数据类型的实现
接下来我们要尝试着实现一些集合类的API,一步一步地来,先试着实现一个容量固定、类型固定切不支持迭代的“定容栈”FixedCapacityStackOfString。示例代码来自Algorithms一书,当中使用到的库的jar包我会贴在文章末尾,我传了一份,不过CSDN上传的资源不得不最少收1个积分,我会把官网下载的链接也给贴上。
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class FixedCapacityStackOfStrings {
private String[] a; // 使用数组作为这个栈的数据的表示方式
private int N; // 栈中的元素数量
public FixedCapacityStackOfStrings(int cap) {
a = new String[cap]; // 构造器,新建一个长度为cap的String数组
}
public boolean isEmpty() {
return N == 0; // 如果N为0,则栈为空
}
public int size() {
return N; // 返回N作为栈的大小
}
public void push(String item) {
a[N++] = item; // 新元素添加在数组末尾
}
public String pop() {
return a[--N]; // 从数组末尾取出一个元素,并将栈的大小减1(注意:N表示栈的大小而非数组大小)
}
// 测试用例
public static void main(String[] args) {
FixedCapacityStackOfStrings s;
s = new FixedCapacityStackOfStrings(100);
while (!StdIn.isEmpty()) {
String item = StdIn.readString();
if (!item.equals("-")) {
s.push(item);
} else if (!s.isEmpty()) {
StdOut.print(s.pop() + " ");
}
}
StdOut.println("(" + s.size() + " left on stack)");
}
}这个类的代码再简单不过了,我在代码中也做了详尽的注释,所以不再多讲。其运行结果如下:
(输入)to be or not to - be - - that - - - is
to be not that or be
(2 left on stack)
FixedCapacityStackOfString只是一个很简单的实现,它存在的第一个问题就是其仅仅能处理String型对象,如果需要处理其他类型的值,那我们又需要照猫画虎地实现另一个栈……所以这个实现是没有任何实用价值的,它仅仅是带我们了解一下如何实现一个抽象数据类型。接下来我们要解决这个问题,联想到我们上文提到的泛型,这个问题就迎刃而解了:
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
/**
* 利用泛型实现一个可处理任意数据类型对象的定容栈
* @param - 类型参数,在创建时替换为具体类型
*/
public class FixedCapacityStack
- {
private Item[] a;
private int N;
public FixedCapacityStack(int cap) {
a = (Item[]) new Object[cap]; // Java中,不能实例化泛型数组,因此我们使用了Object型数组再强转为类型参数Item
}
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
public void push(Item item) {
a[N++] = item;
}
public Item pop() {
return a[--N];
}
public static void main(String[] args) {
FixedCapacityStack
s;
s = new FixedCapacityStack(100);
while (!StdIn.isEmpty()) {
String item = StdIn.readString();
if (!item.equals("-")) {
s.push(item);
} else if (!s.isEmpty()) {
StdOut.print(s.pop() + " ");
}
}
StdOut.println("(" + s.size() + " left on stack)");
}
} 就这样,我们对FixedCapacityStackOfString作出改进,现在它可以处理任意数据类型的对象了。当然,这个实现依然不够完善,实际使用中我们更需要集合的大小是随我们传入的对象数量动态改变的,更重要的是,集合类数据类型的重要性质是其可迭代。在实现这两个问题之前,我们先再了解一个概念——对象游离。
对象游离
先来了解一下Java的垃圾回收策略——回收所有无法被访问的对象的内存。在上文代码的实现中,pop()方法在弹出一个元素之后,其实仅仅是将栈的大小标记减1,使我们无法再从栈中访问这个对象,但是这个元素的引用依然存在于栈所持有的数组中,Java虚拟机的垃圾处理器无法得知这个元素永远无法被访问了这一点,于是它将继续占有一块内存造成资源的浪费,这种保存一个不需要的对象的引用的情况,即为游离。要避免对象游离其实也不复杂,只需要用null来覆盖该引用,系统就将知道该引用已无效,该对象的引用被覆盖则意味着它此时已没有了引用,Java的垃圾回收器则会将其内存回收,这也是我们在很多情况下释放完一个对象的资源后还需要将其引用置空的原因。
能够动态调整大小的下压栈
继续上文的两个问题,可动态调节数组大小与迭代。Java的数组一经创建其大小就无法被改变,这是语言的机制决定,想要实现动态调整集合大小就需要另辟蹊径了——谁说我们只能使用一个数组来存储元素呢?我们可以考虑在添加元素(push)时,检查原数组大小,若是此时剩余空间不多了,便再创建一个数组,将原数组的元素移动到新的数组中,再将原数组的引用指向新的数组,Java的垃圾回收器可回收原数组:
private void resize(int max) {
Item[] temp = (Item[]) new Object[max];
for (int i = 0; i < N; i++) {
temp[i] = a[i];
}
a = temp;
}至于迭代,上文已经说过,实现Iterable接口即可。所以完整的数据类型实现如下:
import java.util.Iterator;
public class ResizingArrayStack- implements Iterable
- {
private Item[] a = (Item[]) new Object[1];
private int N = 0;
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
public void push(Item item) {
if (N == a.length) {
resize(a.length * 2); // 当栈的大小与数组长度相等时,将数组大小调整至原先的两倍以便有充足的空间继续添加元素
}
a[N++] = item;
}
public Item pop() {
Item item = a[--N];
a[N] = null; // 重置栈顶元素的引用,使其能被回收
if (N > 0 && N == a.length / 4) {
resize(a.length / 2); // 当栈的大小等于数组大小的1/4时,将数组大小调整至原先的1/2以节省资源
}
return item;
}
private void resize(int max) {
Item[] temp = (Item[]) new Object[max];
for (int i = 0; i < N; i++) {
temp[i] = a[i];
}
a = temp;
}
@Override
public Iterator
- iterator() {
return new ReverseArrayIterator();
}
class ReverseArrayIterator implements Iterator
- {
private int i = N;
@Override
public boolean hasNext() {
return i > 0;
}
@Override
public Item next() {
return a[--i]; // 获取到的下一个元素总是栈顶元素
}
@Override
public void remove() {
}
}
}
再简单说说Iterable接口。实现Iterable接口,需要重写一个方法:
Iterator- iterator();
需要在这个方法中返回一个迭代器Iterator,在示例代码中,我们定义了一个名为ReverseArrayIterator的迭代器,其实现了Iterator接口,可以使用它逆序迭代指定数组。关于Iterator,我们通常会实现三个抽象方法:
public interface Iterator {
boolean hasNext();
E next();
default void remove() {
throw new UnsupportedOperationException("remove");
}
}
hasNext()用于迭代中判断是否还有下一个元素,next()将返回下一个元素。本例中我们将remove()方法实现为一个空方法,因为我们并不希望在迭代过程中执行remove操作——当我们在迭代中remove掉数组中的一个元素时,将会导致被删除元素后面的元素向前“移位”,使得后续元素无法被正常处理产生异常。
到这里,我们已经实现了一个简单的下压栈。
链表
上文中利用数组实现了下压栈,实际上是运用了“顺序表”这一基础数据结构,它是以数组的形式、在一段连续的内存空间上来存放数据,它的优势在于可通过索引访问表中任意数据、进行修改,不足之处则是初始化时需要指定这段内存空间的大小,当然我们也可以像上文那样动态调节数组大小,只不过这种方式依然会造成空间的浪费。与顺序表对应的,还有一种被称为单链表的基础数据结构。先来看看链表的定义:
链表是一种递归的数据结构,它或者为空,或者是指向一个节点的引用,该节点含有一个泛型的元素和一个指向另一条链表的引用。
这个定义中,最重要的概念就是递归,程序(过程、方法)调用自身即为递归,例如,我们可以定义如下数据类型:
private class Node {
Item item;
Node next;
}Node类含有两个实例变量,分别为参数类型Item和Node类型——其实例变量的类型又是这个类自身的类型,这即是链表递归的本质。Node类型实际就定义了一个节点,item和next分别为这个节点中的泛型元素和指向另一条链表的引用,当我们使用new来创建一个Node对象时,将会产生一个指向Node对象的引用,它的实例变量item和next都为null,next为null则是表明该节点没有指向下一条链表。构造一个链表也并不困难,如下代码所示:
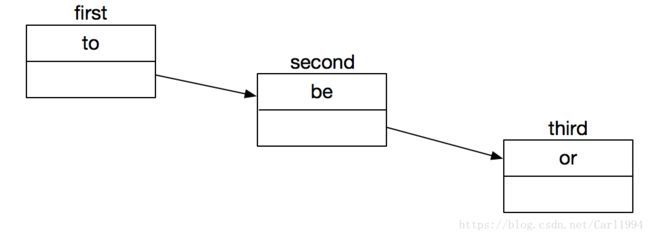
Node first = new Node();
Node second = new Node();
Node third = new Node();
first.item = "to";
second.item = "be";
third.item = "not";
first.next = second;
second.next = third;
以上的代码创建了三个节点,first.next指向second,second.next指向third,third.next保持为null,则可认为节点first是表头,third为表尾,该链表如图所示:
接下来我们试着用单链表来实现下压栈、先进先出队列和背包:
用链表实现下压栈
package iterator;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
import java.util.Iterator;
public class Stack- implements Iterable
- {
private class Node { //①
Item item;
Node next;
}
private Node first; // 栈顶元素
private int N; // 栈的大小
@Override
public Iterator
- iterator() {
return new Iterator
- () {
private Node current = first;
@Override
public boolean hasNext() {
return current != null;
}
@Override
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
@Override
public void remove() {
}
};
}
public Stack() {
}
public void push(Item item) {
Node oldFirst = first;
first = new Node();
first.item = item;
first.next = oldFirst;
N++;
}
public Item pop() {
Item item = first.item;
first = first.next;
N--;
return item;
}
public boolean isEmpty() {
return first == null;
}
public int size() {
return N;
}
// 测试用例
public static void main(String[] args) {
Stack
s;
s = new Stack<>();
while (!StdIn.isEmpty()) {
String item = StdIn.readString();
if (!item.equals("-")) {
s.push(item);
} else if (!s.isEmpty()) {
StdOut.print(s.pop() + " ");
}
}
StdOut.println("(" + s.size() + " left on stack)");
}
}
用链表实现先进先出队列
package iterator;
import java.util.Iterator;
public class Queue- implements Iterable
- {
private class Node {
Item item;
Node next;
}
private Node first;
private Node last;
private int N;
@Override
public Iterator
- iterator() {
return new Iterator
- () {
private Node current = first;
@Override
public boolean hasNext() {
return current != null;
}
@Override
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
};
}
public Queue() {
}
public void enqueue(Item item) {
Node oldLast = last;
last = new Node();
last.item = item;
last.next = null;
if (isEmpty()) {
first = last;
} else {
last.next = oldLast;
}
}
public Item dequeue() {
Item item = first.item;
first = first.next;
if (isEmpty()) {
last = null;
}
N--;
return item;
}
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
}
用链表实现背包
package iterator;
import java.util.Iterator;
import java.util.Spliterator;
import java.util.function.Consumer;
public class Bag- implements Iterable
- {
private class Node {
Item item;
Node next;
}
private Node first;
private int N;
@Override
public Iterator
- iterator() {
return new Iterator
- () {
private Node current = first;
@Override
public boolean hasNext() {
return current != null;
}
@Override
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
};
}
public Bag() {
}
public void add(Item item) {
Node oldFirst = first;
first = new Node();
first.item = item;
first.next = oldFirst;
N++;
}
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
}
与顺序表相比,以单链表实现的集合数据类型不需要提前指定大小,在增、删数据时也不必动态计算数据大小。但是如果要修改集合中的某一个元素的话,单链表只能遍历到该元素再对其进行修改,这样做的耗时与链表长度成正比,显然并非最优解;同样的问题对于顺序表而言,只需要通过索引即可访问指定的数据对其进行修改,并不会有太大资源上的消耗。所以可以总结一下,顺序表的优势在于查询和修改数据,而链表的优势在于插入和删除数据——但是对于单链表来说,在任意位置增、删数据也并不简单,标准的解决方案是使用双向链表,关于双向链表和循环链表以后再讲。
小结
这篇文章简单讲了点算法的基础,主要是介绍了一些基本概念,然后围绕背包、队列和栈引出了顺序表和单链表这两点知识,以及提供了几段以顺序表、单链表实现集合类数据类型的示例代码,这些示例基本都来自《算法》一书。下一篇文章我会写一下算法复杂度相关的知识介绍、总结。
示例中使用到的库:
1.官方下载地址
2.如果嫌麻烦的话可以直接下载我上传的,不过需要1积分