反向传播(BackPropagation)与梯度下降(Gradient Descent)
梯度下降算法(Gradient Descent)
在机器学习的模型的训练阶段,对模型反复做的事情就是将训练样本通过模型计算出的结果与实际训练集的标签进行比对,用以修改模型中的参数,直至模型的计算结果与训练集中的结果一致。
损失函数
为了量化的表现出模型计算结果与实际的差距,因此引入了损失函数(Loss function)用以显示模型的准确率,不断修改模型参数使得损失函数的值降到最小
- 输入:模型
- 输出:模型的优劣
基于统计学的知识,我们可以采用模型计算结果与实际结果的均方差来表示损失函数,下面公式中假设模型 f ( x ) f(x) f(x),损失函数 L ( f ) L(f) L(f), y ^ \hat y y^表示训练集中的标签
L ( f ) = ∑ ( y ^ − f ( x ) ) 2 L(f)=\sum (\hat y-f(x))^2 L(f)=∑(y^−f(x))2
因此,修正模型的任务就转化为了找到最优的模型 f ∗ f^* f∗使得 L ( f ) L(f) L(f)得到最小值。
f ∗ = arg min f L ( f ) f^*=\arg \min_f L(f) f∗=argfminL(f)
而 f ∗ f^* f∗的确定就是 f ( x ) f(x) f(x)中参数的确定。
假设 f ( x ) f(x) f(x)中有两个参数 ω \omega ω, b b b,则 L ( f ) L(f) L(f)可表示为 L ( ω , b ) L(\omega,b) L(ω,b),而上述问题就最终变为
ω ∗ , b ∗ = arg min ω , b L ( ω , b ) \omega^*,b^*=\arg \min_{\omega,b}L(\omega,b) ω∗,b∗=argω,bminL(ω,b)
而寻找最优参数的过程则是使用梯度下降算法
梯度下降
类比想象一个形象一点的过程:一个被随机放在群山中的登山者,在一个看不见前路的黑夜,在对地形一无所知的情况下,如何最快速的从所在位置找到其能找到的最低点呢?
答案是,从所在位置朝下降坡度最大的方向迈步,每迈出一步,判断一下当前位置下降坡度最大的方向,并迈出下一步,直至到达不存在下降坡度的地方。

回到当前的问题,这里的群山就是损失函数,登山者就是模型中的参数,随机放入山中指的是,参数初始为随机值。
找到最低点就是找到最小的损失函数,而登山者的迈步就是不断修改参数值,对任意参数v
v ← v − Δ v v\gets v-\Delta v v←v−Δv
而寻找最大的下降坡度就是计算函数相对于某个参数的梯度,向梯度下降最为明显的方向移动,以前面含两个参数的损失函数为例,对于第n次计算
ω n + 1 = ω n − η ∂ L ∂ ω ∣ ω = ω n b n + 1 = b n − η ∂ L ∂ b ∣ b = b n \omega^{n+1}=\omega^n-\eta\frac{\partial L}{\partial \omega}|_{\omega=\omega^n}\\{}\\ b^{n+1}=b^n-\eta\frac{\partial L}{\partial b}|_{b=b^n} ωn+1=ωn−η∂ω∂L∣ω=ωnbn+1=bn−η∂b∂L∣b=bn
公式中的 η \eta η为学习率(learning rate),可以自行设置的常数,用以控制模型修正的速度
反向传播算法
将梯度下降算法用于神经网络的模型
数学基础——求导链式法则(chain rule)
对于函数 x = g ( s ) , y = h ( s ) , z = f ( x , y ) x=g(s),y=h(s),z=f(x,y) x=g(s),y=h(s),z=f(x,y)
d z d s = ∂ z ∂ x d x d s + ∂ z ∂ y d y d s \frac{\mathrm{d}z}{\mathrm{d}s}=\frac{\partial z}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}s}+\frac{\partial z}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}s} dsdz=∂x∂zdsdx+∂y∂zdsdy
神经网络的梯度下降计算
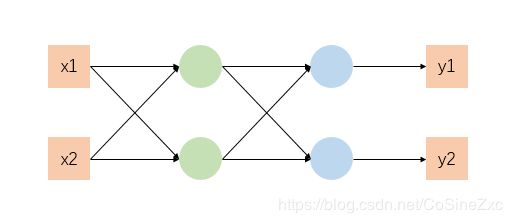
我们以一个结构较为简单的神经网络为例
同样要求得该模型损失函数最小时的参数值,由于神经网络模型中有多个输出,需要将各自输出求和作为总的损失函数。
L ( θ ) = ∑ l ( θ ) L(\theta)=\sum l(\theta) L(θ)=∑l(θ)
求解梯度时,用w代指参数
∂ L ∂ w = ∑ ∂ l ∂ w \frac{\partial L}{\partial w}=\sum \frac{\partial l}{\partial w} ∂w∂L=∑∂w∂l
因此,只需要逐一求解每个输出节点的损失函数梯度
正向传递(forward pass)
对于每个参数而言,将所在的网络层结构细化
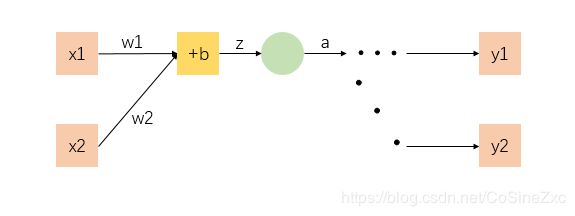
对于每一层的计算
z = w 1 x 1 + w 2 x 2 + b a = σ ( z ) l 1 = f 1 ( a ) l 2 = f 2 ( a ) z=w_1x_1+w_2x_2+b\\ a=\sigma(z)\\ l_1=f_1(a)\\ l_2=f_2(a) z=w1x1+w2x2+ba=σ(z)l1=f1(a)l2=f2(a)
- z z z是输入、系数及偏置(bias)的和
- a a a是将 z z z放入激活函数 a = σ ( z ) a=\sigma(z) a=σ(z),激活函数是人为选择,不同的函数有不同的导数
- a a a不仅作为本层神经网络的输出,也同样是下一层神经网络的输入,因此下一层神经网络与本层操作完全相同,所以 f 1 f 2 f_1f_2 f1f2是对于后面更多层神经网络的简易表示
因此对于每个参数的梯度所需要的最终结果,使用链式法则
∂ l ∂ w n = ∂ z ∂ w n d a d z ∂ l ∂ a \frac{\partial l}{\partial w_n}=\frac{\partial z}{\partial w_n}\frac{\mathrm{d} a}{\mathrm{d} z}\frac{\partial l}{\partial a} ∂wn∂l=∂wn∂zdzda∂a∂l
对于链式法则中的每一项分别求解
∂ z ∂ w n = x n d a d z = σ ′ ( z ) \frac{\partial z}{\partial w_n}=x_n\\{}\\ \frac{\mathrm{d} a}{\mathrm{d} z}=\sigma'(z) ∂wn∂z=xndzda=σ′(z)
第一项的值取决于该层的输入( w n w_n wn收输入影响,偏置b该项永远为1)
第二项的值取决于选择的激活函数
而最后一项则取决于后续更多层神经网络的推导
反向传递(backward pass)
为了细化上一部分未解决的部分推导,将参数所在层的后一部分网络细化
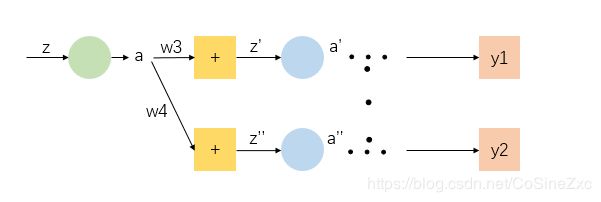
这一部分里面
z ′ = w 3 a + . . . z ′ ′ = w 4 a + . . . a ′ = σ ( z ′ ) a ′ ′ = σ ( z ′ ′ ) z'=w_3a+...\\ z''=w_4a+...\\ a'=\sigma(z')\\ a''=\sigma(z'') z′=w3a+...z′′=w4a+...a′=σ(z′)a′′=σ(z′′)
因此
∂ l ∂ a = ∂ z ′ ∂ a ∂ a ′ ∂ z ′ ∂ l ∂ a ′ + ∂ z ′ ′ ∂ a ∂ a ′ ′ ∂ z ′ ′ ∂ l ∂ a ′ ′ ∂ z ′ ∂ a = w 3 ∂ z ′ ∂ a = w 4 ∂ a ′ ∂ z ′ = σ ′ ( z ′ ) ∂ a ′ ′ ∂ z ′ ′ = σ ′ ( z ′ ′ ) \frac{\partial l}{\partial a}=\frac{\partial z'}{\partial a}\frac{\partial a'}{\partial z'}\frac{\partial l}{\partial a'}+\frac{\partial z''}{\partial a}\frac{\partial a''}{\partial z''}\frac{\partial l}{\partial a''}\\{}\\ \frac{\partial z'}{\partial a}=w_3\\{}\\ \frac{\partial z'}{\partial a}=w_4\\{}\\ \frac{\partial a'}{\partial z'}=\sigma'(z')\\{}\\ \frac{\partial a''}{\partial z''}=\sigma'(z'') ∂a∂l=∂a∂z′∂z′∂a′∂a′∂l+∂a∂z′′∂z′′∂a′′∂a′′∂l∂a∂z′=w3∂a∂z′=w4∂z′∂a′=σ′(z′)∂z′′∂a′′=σ′(z′′)
将已知部分化繁为简
∂ l ∂ a = F ( ∂ l ∂ a ′ , ∂ l ∂ a ′ ′ ) \frac{\partial l}{\partial a}=F(\frac{\partial l}{\partial a'},\frac{\partial l}{\partial a''}) ∂a∂l=F(∂a′∂l,∂a′′∂l)
由此可见, ∂ l / ∂ a n \partial l/\partial a^n ∂l/∂an的计算存在递归的性质。
因此,按照递归的方式分为以下两种情况
- z n z^n zn位于网络的最后一层,经过激活函数后直接输出
- z n z^n zn没有位于网络的最后一层,通过后续计算得出
若位于神经网络的最后一层
∂ l ∂ z ′ = d y 1 d z ′ d l d y 1 \frac{\partial l}{\partial z'}=\frac{\mathrm{d} y_1}{\mathrm{d} z'}\frac{\mathrm{d} l}{\mathrm{d} y_1} ∂z′∂l=dz′dy1dy1dl
分解后的两项均可计算,分别取决于所选的激活函数和损失函数
若并非位于神经网络的最后一层
则根据需要接下来的网络计算时的结果作为输入,递归运算。
反向传播
根据上面的推导,我们可以看出:靠前的网络层的部分取值取决于后面的结果

也就是说
∂ l ∂ a ← ∂ l ∂ a ′ ← ∂ l ∂ a ′ ′ \frac{\partial l}{\partial a}\gets \frac{\partial l}{\partial a'}\gets \frac{\partial l}{\partial a''} ∂a∂l←∂a′∂l←∂a′′∂l
总结
最终将forward pass 和 backward pass 过程中计算出的结果进行合并
∂ l ∂ w = ∂ l ∂ a ∂ a ∂ w \frac{\partial l}{\partial w}=\frac{\partial l}{\partial a}\frac{\partial a}{\partial w} ∂w∂l=∂a∂l∂w∂a
参考资料
李宏毅机器学习(2017)