【NOI2013模拟】梦醒

Description:

Pty继续着他的疯狂奔跑，终于渐渐体力不支，在一个应该拐弯的地方没有刹住车，掉入了深深的沼泽中，“啊~~~~~·”pty惊恐的大叫，突然从梦中惊醒了。哪里还有什么奇怪的金字塔，沼泽地，大树。。。只是一个梦而已呀。看了看自己熟悉的房间，pty定了定神。

好不容易恢复了过来，pty突然想到还有集训队的互测题没有出！！，如果没有出完的话，后果= =。。啧啧。。pty宁愿再回到金字塔去。于是pty想啊想，找啊找，找到了一道傻逼题：

给定一个矩阵A：n行m列，一个矩阵B：h行w列，在B矩阵中有一个特殊的位置为(x,y)。现在可以从A矩阵中选出一个大小和B相等的区域，设选出的矩阵为C，那么花费的代价是

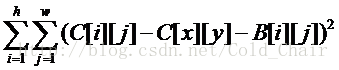
现在pty想知道在A矩阵中选出的所有C矩阵中前K小的代价分别是多少。

题解：

拆个式子先。

设c=c[i][j],c’=c[x][y],b=b[i][j]

则 (c−c′−b)2 ( c − c ′ − b ) 2
=c2+c′2+b2 = c 2 + c ′ 2 + b 2
−2cc′−2bc+2bc′ − 2 c c ′ − 2 b c + 2 b c ′

发现除了bc都可以快速维护。

观察一下bc：

∑wi=1∑hj=1c[i][j]∗b[i][j] ∑ i = 1 w ∑ j = 1 h c [ i ] [ j ] ∗ b [ i ] [ j ]

这个东西似乎不好直接搞。

设b’[w-i][h-j]=b[i][j]

这样变换以后把i消掉，你发现坐标相加就是(w,h)

所以用FFT求c*b’，就可以求出以每个点为右下角的b*c了。

我们知道FFT涉及到负数运算，常数较大。

发现答案较小，可以直接上NTT。

有负数怎么办呢？

注意到答案还会小于mo/2

所以如果答案大于mo/2,它就是负数了，这是一个技巧。

Code：

#include 
#include
#define ll long long
#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define ff(i, x, y) for(int i = x; i < y; i ++)
using namespace std;

const ll mo = 998244353;

const int N = 667;

int n, m, a[N][N];
int w, h, b[N][N], x, y, k;
int f1[N][N], f2[N][N];
int sb1, sb2;

ll c[N * N * 8], d[N * N * 8], n0, W[N * N * 8], tx;

ll ksm(ll x, ll y) {
    ll s = 1;
    for(; y; y /= 2, x = x * x % mo)
        if(y & 1) s = s * x % mo;
    return s;
}
void dft(ll *a, int n) {
    ff(i, 0, n)  {
        int p = i, q = 0;
        ff(j, 0, tx) q = q * 2 + p % 2, p /= 2;
        if(q > i) swap(a[q], a[i]);
    }
    for(int m = 2; m <= n; m *= 2) {
        int h = m / 2;
        ff(i, 0, h) {
            ll w = W[i * (n / m)];
            for(int j = i; j < n; j += m) {
                int k = j + h;
                ll u = a[j], v = a[k] * w % mo;
                a[j] = (u + v) % mo; a[k] = (u - v + mo) % mo;
            }
        }
    }
}
void fft(ll *a, ll *b, int n) {
    ll rev = ksm(3, (mo - 1) / n);
    W[0] = 1; fo(i, 1, n) W[i] = W[i - 1] * rev % mo;
    dft(a, n); dft(b, n);
    ff(i, 0, n) a[i] *= b[i];
    fo(i, 0, n / 2) swap(W[i], W[n - i]);
    dft(a, n); ll ni = ksm(n, mo - 2);
    ff(i, 0, n) a[i] = a[i] * ni % mo;
}

struct node {
    int x, y, ans;
} e[N * N];
int tot;

bool cmp(node a, node b) {
    if(a.ans < b.ans) return 1;
    if(a.ans > b.ans) return 0;
    if(a.x < b.x) return 1;
    if(a.x > b.x) return 0;
    return a.y < b.y;
}

int main() {
    scanf("%d %d", &n, &m);
    fo(i, 1, n) {
        fo(j, 1, m) {
            scanf("%d", &a[i][j]);
            f1[i][j] = f1[i - 1][j] + f1[i][j - 1] - f1[i - 1][j - 1] + a[i][j];
            f2[i][j] = f2[i - 1][j] + f2[i][j - 1] - f2[i - 1][j - 1] + a[i][j] * a[i][j];
        }
    }
    scanf("%d %d", &w, &h);
    fo(i, 1, w) {
        fo(j, 1, h) {
            scanf("%d", &b[i][j]);
            sb1 += b[i][j]; sb2 += b[i][j] * b[i][j];
        }
    }
    scanf("%d %d %d", &x, &y, &k);
    fo(i, 1, n) fo(j, 1, m) c[i * m + j] = a[i][j];
    fo(i, 1, w) fo(j, 1, h) d[(w - i) * m + h - j] = b[i][j];
    n0 = n * m; tx = 0; while(1 << tx ++ < n0); n0 = 1 << tx;
    ff(i, 0, n0) c[i] += (c[i] < 0) * mo, d[i] += (d[i] < 0) * mo;
    fft(c, d, n0);
    fo(i, 1, n) fo(j, 1, m) {
        int num = i * m + j;
        b[i][j] = c[num] > mo / 2 ? c[num] - mo : c[num];
    }
    x --; y --;
    fo(i, 1, n - w + 1) fo(j, 1, m - h + 1) {
        int u = i + w - 1, v = j + h - 1;
        tot ++;
        e[tot].x = i; e[tot].y = j;
        e[tot].ans = a[i + x][j + y] * a[i + x][j + y] * w * h;
        e[tot].ans += sb2 + f2[u][v] - f2[i - 1][v] - f2[u][j - 1] + f2[i - 1][j - 1];
        e[tot].ans += 2 * sb1 * a[i + x][j + y];
        e[tot].ans -= 2 * (f1[u][v] - f1[i - 1][v] - f1[u][j - 1] + f1[i - 1][j - 1]) * a[i + x][j + y];
        e[tot].ans -= 2 * b[u][v];
    }
    sort(e + 1, e + tot + 1, cmp);
    fo(i, 1, k) printf("%d %d %d\n", e[i].x, e[i].y, e[i].ans);
}